20.2.2 平均数、中位数和众数的选用 课件(共28张PPT)
文档属性
| 名称 | 20.2.2 平均数、中位数和众数的选用 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 20:49:21 | ||
图片预览




文档简介
(共28张PPT)
20.2.2 平均数、中位数和众数的选用
华师大版 八年级 下册
教学目标
教学目标:1.进一步认识平均数、中位数、众数都可以反映一组数据的集
中趋势的思想;
2.了解平均数、中位数、众数各自的特点,能选择适当的量反
映数据的集中趋势.
教学重点:平均数、中位数和众数的特性及它们的灵活应用.
教学难点:平均数、中位数和众数的灵活运用.
新知导入
情境引入
应聘者小王
第二天,小王上班了。
职员B
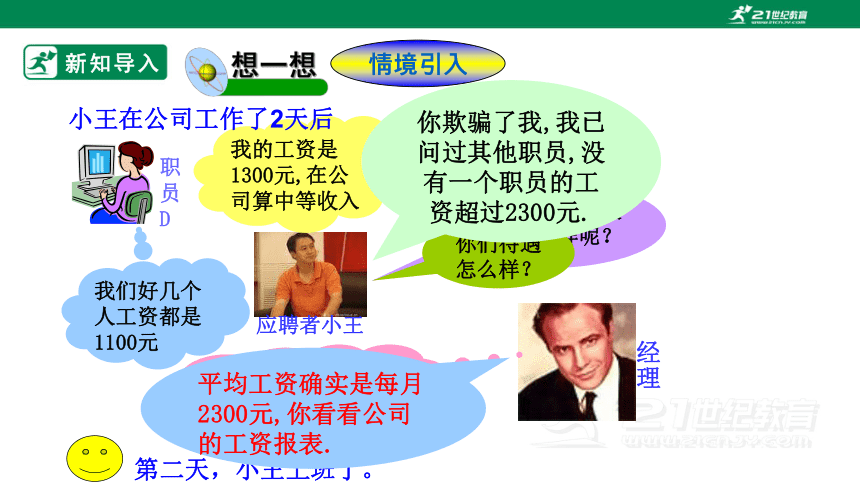
我的工资是1300元,在公司算中等收入
我们好几个人工资都是1100元
职员D
你们公司员工收入到底怎样呢?
经理
我这里报酬不错, 月平均工资是2300元,你在这儿好好干!
小王在公司工作了2天后
你们待遇怎么样?
你欺骗了我,我已问过其他职员,没有一个职员的工资超过2300元.
平均工资确实是每月2300元,你看看公司的工资报表.
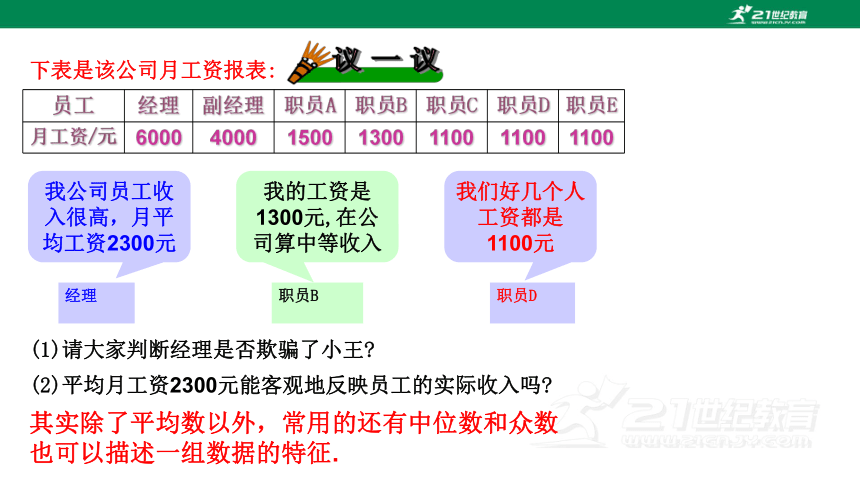
下表是该公司月工资报表:
经理
职员B
职员D
(1)请大家判断经理是否欺骗了小王
(2)平均月工资2300元能客观地反映员工的实际收入吗
其实除了平均数以外,常用的还有中位数和众数
也可以描述一组数据的特征.
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E
月工资/元 6000 4000 1500 1300 1100 1100 1100
我公司员工收入很高,月平均工资2300元
我的工资是1300元,在公司算中等收入
我们好几个人工资都是1100元
新知讲解
合作学习
八年级某班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的5次数学成绩分别是:
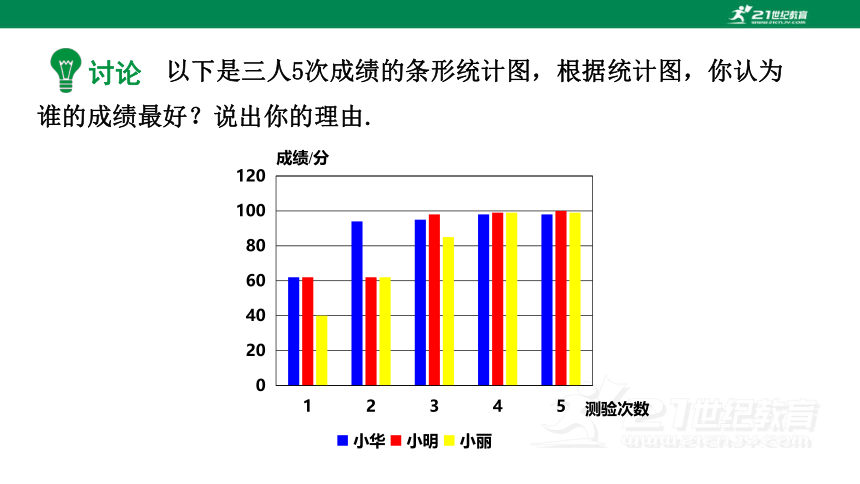
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的成绩比另两位同学好,你知道他们的依据分别是什么吗?
分别找出三位同学5次成绩的平均数、中位数、众数,进行比较.
问题1
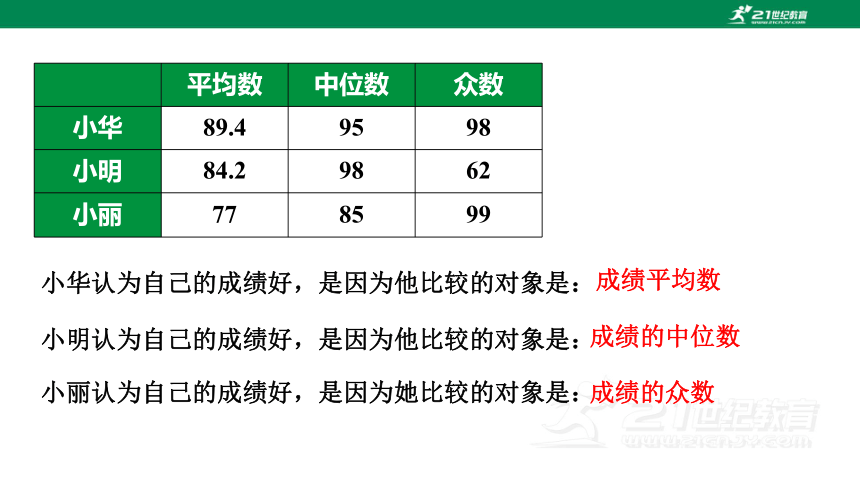
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
小华认为自己的成绩好,是因为他比较的对象是:
小明认为自己的成绩好,是因为他比较的对象是:
小丽认为自己的成绩好,是因为她比较的对象是:
成绩平均数
成绩的中位数
成绩的众数
以下是三人5次成绩的条形统计图,根据统计图,你认为谁的成绩最好?说出你的理由.
成绩/分
测验次数
讨论
思考
高一级学校录取新生主要是依据考生的总分,这与平均数、中位数和众数中的哪一个关系较大?谁更容易被录取?
成绩平均数
小华
问题2
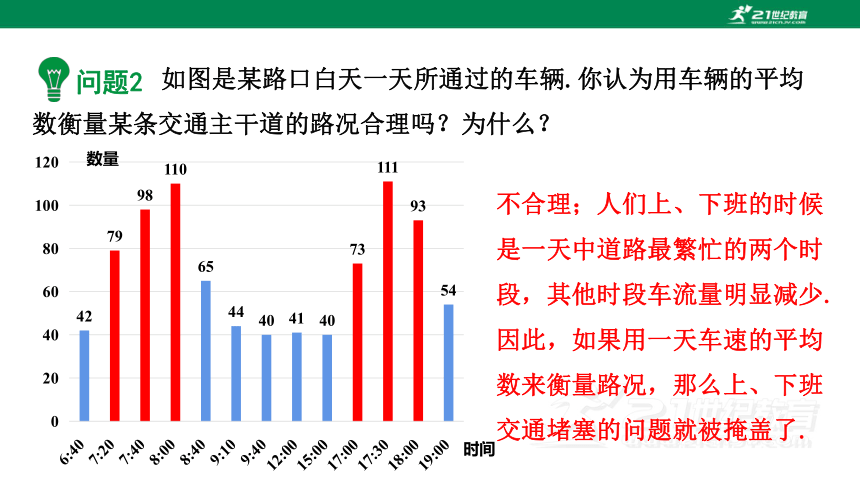
如图是某路口白天一天所通过的车辆.你认为用车辆的平均数衡量某条交通主干道的路况合理吗?为什么?
不合理;人们上、下班的时候是一天中道路最繁忙的两个时段,其他时段车流量明显减少.因此,如果用一天车速的平均数来衡量路况,那么上、下班交通堵塞的问题就被掩盖了.
数量
时间
如何正确衡量某路口一天的路况?
思考
按道路繁忙的不同程度,将一天分为几个时段分别计算平均车速.如:将早晚高峰时间和其他时间分开进行计算.
数量
时间
提炼概念
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息;但它受极端值的影响较大,任何一个数据的变动都会相应地引起平均数的变动.
请说说平均数、众数和中位数这三个统计量的各自特点.
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,缺点是当众数有多个且众数的频数相对较小时可靠性小,局限性大.
中位数的计算很少,仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给的数据中.当一组数据中的个别数据变动较大时,可用中位数描述其趋势.
典例精讲
例1 (1)草地上有6个人正在玩游戏,他们年龄的平均数是15岁,请想象一下是怎样年龄的6个人在玩游戏?
解:通常人们会想象是一群中学生在玩游戏,但是,如果是一个65岁的大娘领着5个5岁的孩子在玩游戏也是有可能的嘛!这是一个不适合用平均数而适合用众数或中位数代表一组数据的例子,大娘的年龄把平均年龄一下子给抬上去了.
(2)为筹备班级的新年晚会,班长对全班同学爱吃香蕉、橘子、柚子中的哪一种水果作了民意调查. 最终买什么水果,该由调查的平均数,众数还是中位数决定呢?
解:显然是由众数决定好,因为它代表了全班多数同学的意愿.
(3)八年级有4个班级,如果已知在一次测验中这4个班级每班学生的平均分,也知道各班级的学生人数,那么,我们可以计算出整个年级的平均分,但是,如果已知的是每个班级学生成绩的中位数或者众数,那么我们能得出整个年级的中位数或者众数吗?
解:我们没有办法得出整个年级的中位数或者众数.
归纳概念
平均数、中位数和众数都是反映一组数据集中趋势的量
平均数反映数据的“平均水平”,是最常用的指标.容易受到这组数据中的最大(小)值的影响
中位数反映数据的“中等水平”,求中位数时应先将数据按照大小顺序排列,则正中间的数就是这组数据的中位数
众数反映数据的“多数水平”,一组数据可能有一个或多个众数也可能没有众数
想了解一组数据的平均水平,可计算其平均数;当一组数据中不少数据多次重复出现时,往往关注其众数;当一组数据中个别数据变动较大时,可用中位数来描述其集中趋势
课堂练习
则这些队员投中次数的众数、中位数和平均数分别为( )
A.5,6,6 B.2,6,6
C.5,5,6 D.5,6,5
1.某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如下表:
A
投中次数 3 5 6 7 8
人数 1 3 2 2 2
2.在一次体检中,甲、乙、丙、丁四位同学的平均身高为1.65米,而甲、乙、丙三位同学的平均身高为1.63米,下列说法一定正确的是( )
A.四位同学身高的中位数一定是其中一位同学的身高
B.丁同学的身高一定高于其他三位同学的身高
C.丁同学的身高为1.71米
D.四位同学身高的众数一定是1.65米
C
3.甲、乙两名运动员在6次百米跑训练中的成绩如下:
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
请你比较这两组数据的众数,平均数和中位数,再作判断.
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣.
解:甲:平均数:10.9,众数:10.8,中位数:10.85;
乙:平均数:10.8,众数:10.9,中位数:10.85.
从平均数看,甲的成绩比乙的好;从众数看,乙的成绩比甲的好;从中位数看两人成绩一样.
4.某公司销售部有营销人员15人,销售部为了制定某种
商品的月销售定额,统计了这15天某月的销售量如下:
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售负责人把每位营销员的月销售额定为320件,
你认为是否合理 为什么 如不合理,请你制定一个较合理
的销售定额,并说明理由.
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
320件
平均数是 ,中位数是 ,众数是 .
210件
210件
不合理
因为15人中有13人的销售额不到320件,320件虽是所给数据的平均数,但它却不能很好地反映销售人员的一般水平.
销售额定为210件合适些,因为210件既是中位数,又是众数,
是大部分销售人员能达到的定额.
5. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的
成绩整理并绘制成如图所
示的统计图:
请根据以上信息解答下列问题:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
解:(1)25-6-12-5=2(人),补图如右
(2)a=87.6,b=90,c=100
(3)①一班和二班平均数相等,一班的中位数大于二班
的中位数,故一班的成绩好于二班;
②一班和二班平均数相等,一班的众数小于二班的众
数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的
成绩好于二班
课堂总结
平均数、中位数
与众数的选用
平均数、中位数、众数的特征
平均数、中位数、众数的实际应用及选择策略
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
20.2.2 平均数、中位数和众数的选用
华师大版 八年级 下册
教学目标
教学目标:1.进一步认识平均数、中位数、众数都可以反映一组数据的集
中趋势的思想;
2.了解平均数、中位数、众数各自的特点,能选择适当的量反
映数据的集中趋势.
教学重点:平均数、中位数和众数的特性及它们的灵活应用.
教学难点:平均数、中位数和众数的灵活运用.
新知导入
情境引入
应聘者小王
第二天,小王上班了。
职员B
我的工资是1300元,在公司算中等收入
我们好几个人工资都是1100元
职员D
你们公司员工收入到底怎样呢?
经理
我这里报酬不错, 月平均工资是2300元,你在这儿好好干!
小王在公司工作了2天后
你们待遇怎么样?
你欺骗了我,我已问过其他职员,没有一个职员的工资超过2300元.
平均工资确实是每月2300元,你看看公司的工资报表.
下表是该公司月工资报表:
经理
职员B
职员D
(1)请大家判断经理是否欺骗了小王
(2)平均月工资2300元能客观地反映员工的实际收入吗
其实除了平均数以外,常用的还有中位数和众数
也可以描述一组数据的特征.
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E
月工资/元 6000 4000 1500 1300 1100 1100 1100
我公司员工收入很高,月平均工资2300元
我的工资是1300元,在公司算中等收入
我们好几个人工资都是1100元
新知讲解
合作学习
八年级某班的教室里,三位同学正在为谁的数学成绩最好而争论,他们的5次数学成绩分别是:
小华:62,94,95,98,98;
小明:62,62,98,99,100;
小丽:40,62,85,99,99.
他们都认为自己的成绩比另两位同学好,你知道他们的依据分别是什么吗?
分别找出三位同学5次成绩的平均数、中位数、众数,进行比较.
问题1
平均数 中位数 众数
小华 89.4 95 98
小明 84.2 98 62
小丽 77 85 99
小华认为自己的成绩好,是因为他比较的对象是:
小明认为自己的成绩好,是因为他比较的对象是:
小丽认为自己的成绩好,是因为她比较的对象是:
成绩平均数
成绩的中位数
成绩的众数
以下是三人5次成绩的条形统计图,根据统计图,你认为谁的成绩最好?说出你的理由.
成绩/分
测验次数
讨论
思考
高一级学校录取新生主要是依据考生的总分,这与平均数、中位数和众数中的哪一个关系较大?谁更容易被录取?
成绩平均数
小华
问题2
如图是某路口白天一天所通过的车辆.你认为用车辆的平均数衡量某条交通主干道的路况合理吗?为什么?
不合理;人们上、下班的时候是一天中道路最繁忙的两个时段,其他时段车流量明显减少.因此,如果用一天车速的平均数来衡量路况,那么上、下班交通堵塞的问题就被掩盖了.
数量
时间
如何正确衡量某路口一天的路况?
思考
按道路繁忙的不同程度,将一天分为几个时段分别计算平均车速.如:将早晚高峰时间和其他时间分开进行计算.
数量
时间
提炼概念
平均数的计算要用到所有的数据,它能够充分利用数据提供的信息;但它受极端值的影响较大,任何一个数据的变动都会相应地引起平均数的变动.
请说说平均数、众数和中位数这三个统计量的各自特点.
众数是当一组数据中某一数据重复出现较多时,人们往往关心的一个量,众数不受极端值的影响,这是它的一个优势,缺点是当众数有多个且众数的频数相对较小时可靠性小,局限性大.
中位数的计算很少,仅与数据的排列位置有关,不易受极端值影响,中位数可能出现在所给数据中,也可能不在所给的数据中.当一组数据中的个别数据变动较大时,可用中位数描述其趋势.
典例精讲
例1 (1)草地上有6个人正在玩游戏,他们年龄的平均数是15岁,请想象一下是怎样年龄的6个人在玩游戏?
解:通常人们会想象是一群中学生在玩游戏,但是,如果是一个65岁的大娘领着5个5岁的孩子在玩游戏也是有可能的嘛!这是一个不适合用平均数而适合用众数或中位数代表一组数据的例子,大娘的年龄把平均年龄一下子给抬上去了.
(2)为筹备班级的新年晚会,班长对全班同学爱吃香蕉、橘子、柚子中的哪一种水果作了民意调查. 最终买什么水果,该由调查的平均数,众数还是中位数决定呢?
解:显然是由众数决定好,因为它代表了全班多数同学的意愿.
(3)八年级有4个班级,如果已知在一次测验中这4个班级每班学生的平均分,也知道各班级的学生人数,那么,我们可以计算出整个年级的平均分,但是,如果已知的是每个班级学生成绩的中位数或者众数,那么我们能得出整个年级的中位数或者众数吗?
解:我们没有办法得出整个年级的中位数或者众数.
归纳概念
平均数、中位数和众数都是反映一组数据集中趋势的量
平均数反映数据的“平均水平”,是最常用的指标.容易受到这组数据中的最大(小)值的影响
中位数反映数据的“中等水平”,求中位数时应先将数据按照大小顺序排列,则正中间的数就是这组数据的中位数
众数反映数据的“多数水平”,一组数据可能有一个或多个众数也可能没有众数
想了解一组数据的平均水平,可计算其平均数;当一组数据中不少数据多次重复出现时,往往关注其众数;当一组数据中个别数据变动较大时,可用中位数来描述其集中趋势
课堂练习
则这些队员投中次数的众数、中位数和平均数分别为( )
A.5,6,6 B.2,6,6
C.5,5,6 D.5,6,5
1.某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如下表:
A
投中次数 3 5 6 7 8
人数 1 3 2 2 2
2.在一次体检中,甲、乙、丙、丁四位同学的平均身高为1.65米,而甲、乙、丙三位同学的平均身高为1.63米,下列说法一定正确的是( )
A.四位同学身高的中位数一定是其中一位同学的身高
B.丁同学的身高一定高于其他三位同学的身高
C.丁同学的身高为1.71米
D.四位同学身高的众数一定是1.65米
C
3.甲、乙两名运动员在6次百米跑训练中的成绩如下:
甲(秒) 10.8 10.9 11.0 10.7 11.2 10.8
乙(秒) 10.9 10.9 10.8 10.8 10.5 10.9
请你比较这两组数据的众数,平均数和中位数,再作判断.
分析:谈看法实质上就是按众数,平均数和中位数的大小比较其优劣.
解:甲:平均数:10.9,众数:10.8,中位数:10.85;
乙:平均数:10.8,众数:10.9,中位数:10.85.
从平均数看,甲的成绩比乙的好;从众数看,乙的成绩比甲的好;从中位数看两人成绩一样.
4.某公司销售部有营销人员15人,销售部为了制定某种
商品的月销售定额,统计了这15天某月的销售量如下:
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售负责人把每位营销员的月销售额定为320件,
你认为是否合理 为什么 如不合理,请你制定一个较合理
的销售定额,并说明理由.
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
320件
平均数是 ,中位数是 ,众数是 .
210件
210件
不合理
因为15人中有13人的销售额不到320件,320件虽是所给数据的平均数,但它却不能很好地反映销售人员的一般水平.
销售额定为210件合适些,因为210件既是中位数,又是众数,
是大部分销售人员能达到的定额.
5. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的
成绩整理并绘制成如图所
示的统计图:
请根据以上信息解答下列问题:
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
解:(1)25-6-12-5=2(人),补图如右
(2)a=87.6,b=90,c=100
(3)①一班和二班平均数相等,一班的中位数大于二班
的中位数,故一班的成绩好于二班;
②一班和二班平均数相等,一班的众数小于二班的众
数,故二班的成绩好于一班;
③B级以上(包括B级)一班18人,二班12人,故一班的
成绩好于二班
课堂总结
平均数、中位数
与众数的选用
平均数、中位数、众数的特征
平均数、中位数、众数的实际应用及选择策略
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
