3.1建立一元一次方程模型课件
图片预览






文档简介
课件23张PPT。3.1 建立 一元一次方程模型(1)甲、乙两站之间的高速铁路长1068km,“和谐号”高速列车从甲站开出2.5h后,离乙站还有318km. 该高速列车的平均速度是多少?问题1:请你表示出下面两个问题中的等量关系.设高速列车的平均速度为x km/h,我们可以
用含x的式子表示上述等量关系,即
2.5x+318=1068这个问题等量关系是:
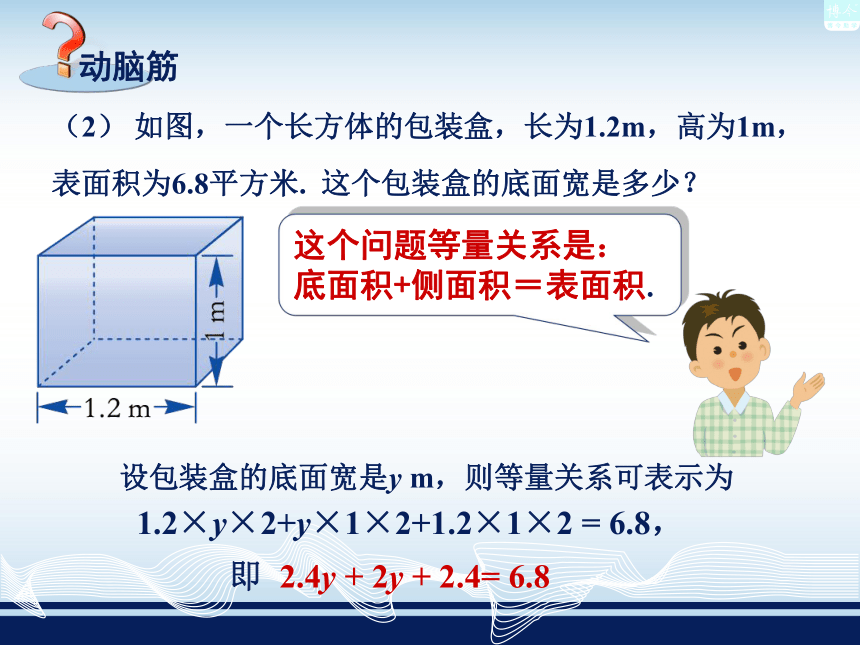
已行驶的路程+剩余的路程= 全长.(2)?如图,一个长方体的包装盒,长为1.2m,高为1m,表面积为6.8平方米. 这个包装盒的底面宽是多少?设包装盒的底面宽是y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,即 2.4y + 2y + 2.4= 6.8这个问题等量关系是:
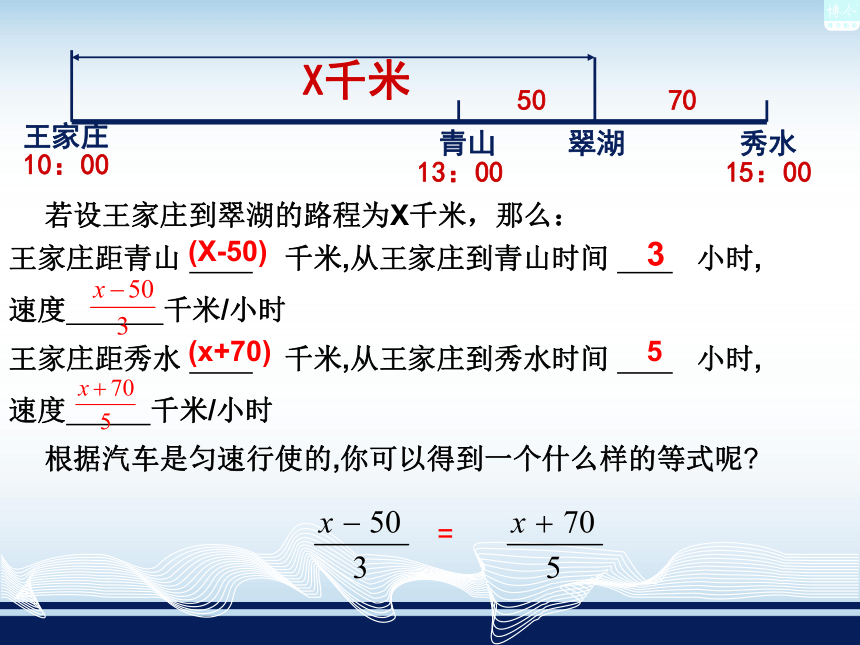
底面积+侧面积=表面积.问题2:一辆旅游汽车匀速行驶,途经王家庄,青山,秀水三地的时间如表所示,翠湖在青山、秀水两地之间, 距青山50千米,距秀水70千米,王家庄到翠湖的路程有多远?5070王家庄青山翠湖秀水10:0013:0015:00解:答:王家庄到翠湖的路程是230千米.王家庄距青山 千米,从王家庄到青山时间 小时,
速度 千米/小时王家庄距秀水 千米,从王家庄到秀水时间 小时,
速度 千米/小时
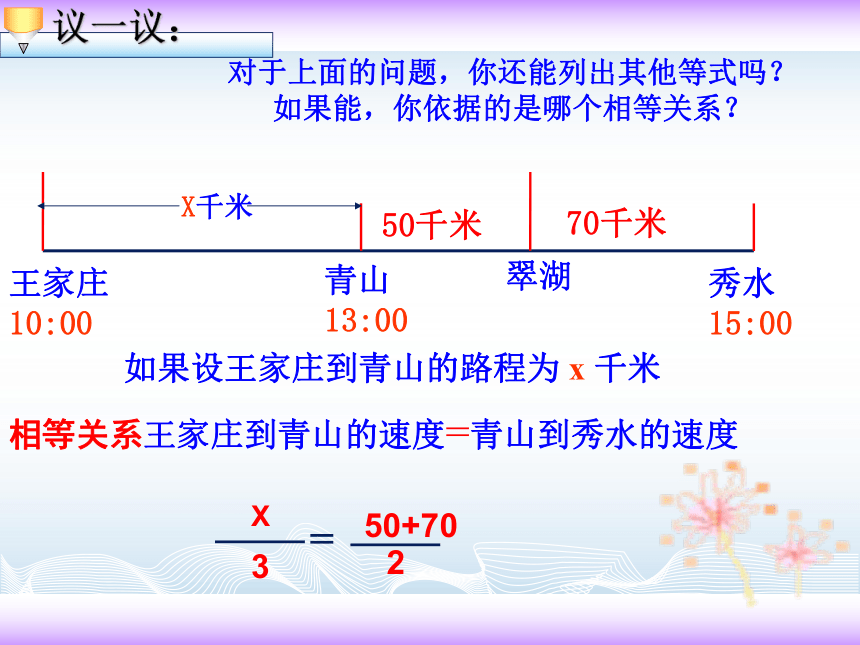
根据汽车是匀速行使的,你可以得到一个什么样的等式呢?(X-50)3(x+70)5=X千米若设王家庄到翠湖的路程为X千米,那么:相等关系王家庄到青山的速度=青山到秀水的速度如果设王家庄到青山的路程为 x 千米对于上面的问题,你还能列出其他等式吗?如果能,你依据的是哪个相等关系?列算式:只用已知数,列出算式表示计算程序,依据是问题中
的数量关系;如:
列方程:可用未知数,表示相等关系,依据是问题中的等量关系.在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.,2.4y + 2y + 2.4= 6.8也是方程。=把所要求的量用字母x(或y,···)表示,根据问题中的等量关系列出方程的过程,叫建立方程模型。问题3:
(1) 上述所列出的方程中含有几个未知数?是谁?
(2)含有未知数的项的次数是几?只含有一个未知数(元),含有未知数的项的次数都是1(次),这样的方程叫做一元一次方程.叫一元一次方程。能使方程左、右两边相等的未知数的值.叫方程的解。求方程的解的过程叫解方程。检验下列x的值是否是方程2.5x+318=1068的解
(1)x=300; (2)x=330.解:(1)把x=300代入原方程得,左边=
左边=右边,所以x=300是方程2.5x+318=1068的解(2)把x=330代入原方程得,左边=
左边 右边,所以x=330不是方程2.5x+318=1068的解2.5×330+318=11432.5×300+318=1068≠1.奥运村奠基仪式上种了一棵树,刚移栽时,树高为2m,假设以后平均每年长0.3m,几年后树高为5m?
设x年后树高为5m,可列出方程______________2.初一年级的女生占全年级学生数的52%,比全年级的男生多31人,初一年级共有多少学生?设初一年级共有学生x人,可列出方程 ______________3.根据下列问题,设未知数并列出方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?设边长为xcm设有x名学生1.判断下列方程是不是一元一次方程:(1)、(3)、(4)、(6)是一元一次方程.2.2008年北京奥运会的足球分赛场——秦皇岛市奥体中心体育场,其足球场的周长为344米,长和宽之差为36米,这个足球场的长与宽分别是多少米?请列出方程.解:设这个足球场的长为x米,则宽为(x-36)米.3.2008年北京奥运会志愿者报名中,某地区女士报名占该地区全部志愿者报名数的52%,比男士多80人,这个地区有多少志愿者报名?请列出方程.解:设这个地区有x名志愿者,则女士报名者有52%x人,男士报名者有(52%x-80)人.1枝钢笔比一枝铅笔多4元,应找你2元买4枝铅笔和一枝钢笔4、小英拿10元钱去买钢笔和铅笔。下面是小英与营业员的对话,你能根据她们的对话内容算出铅笔是多少钱1支吗?买4枝铅笔的钱+买一枝钢笔的钱=10-24x+(x+4)10-2=设1枝铅笔x元,得方程解例1 关于x的方程2(x-1)-a=0的解是3,则a的值是 ( ).
A.4 B.-4 C. 5 D.-5 本题中,应用方程的解的概念解题.把 x=3代入方程,得
2(3-1)-a=0
解之,得 a=4
故,应选择AA解例2 利用方程的定义对四个选项进行判断可知应选择D,因为D中不含未知数,它不符合方程的定义.
故,应选择D. 下列说法错误的是 ( ).
A. 3x-2x=5x是方程 B. x=0是方程
C. 2x-3y=1是方程 D. π=3.14是方程D问题1:这节课我们研究的主要内容是什么?问题2:用方程的方法来解决实际问题,一般要经历哪几个步骤?问题3:算术方法解题和用方程解题的区别是什么?(1)形式上,一个是算式,一个是含未知数的等式(方程);(2)列出的算式只能含有已知数,而方程中既含有已知数,又含有用字母表示的未知数;(3)思考问题的角度不同,前者是用已知数表示未知数,适用于关系简单的问题;后者重在寻找题中的等量关系,借助于字母表示未知数,列式表示等量关系.都是一种用于解决问题的工具. 根据下列问题,设未知数并列出方程1、 一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的修检时间2450小时?2、用一根长24cm的铁丝围成一个长方形,使它长是宽的1.5倍,长方形的长,宽各应是多少?3、某校女生占全体学生的52%,比男生多80人,这个学校有多少学生?4、一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,求上底.5、若方程是 一元一次方程,求m的值。 课外练习为下列各题建立一元一次方程:考考你1.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?
用含x的式子表示上述等量关系,即
2.5x+318=1068这个问题等量关系是:
已行驶的路程+剩余的路程= 全长.(2)?如图,一个长方体的包装盒,长为1.2m,高为1m,表面积为6.8平方米. 这个包装盒的底面宽是多少?设包装盒的底面宽是y m,则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8,即 2.4y + 2y + 2.4= 6.8这个问题等量关系是:
底面积+侧面积=表面积.问题2:一辆旅游汽车匀速行驶,途经王家庄,青山,秀水三地的时间如表所示,翠湖在青山、秀水两地之间, 距青山50千米,距秀水70千米,王家庄到翠湖的路程有多远?5070王家庄青山翠湖秀水10:0013:0015:00解:答:王家庄到翠湖的路程是230千米.王家庄距青山 千米,从王家庄到青山时间 小时,
速度 千米/小时王家庄距秀水 千米,从王家庄到秀水时间 小时,
速度 千米/小时
根据汽车是匀速行使的,你可以得到一个什么样的等式呢?(X-50)3(x+70)5=X千米若设王家庄到翠湖的路程为X千米,那么:相等关系王家庄到青山的速度=青山到秀水的速度如果设王家庄到青山的路程为 x 千米对于上面的问题,你还能列出其他等式吗?如果能,你依据的是哪个相等关系?列算式:只用已知数,列出算式表示计算程序,依据是问题中
的数量关系;如:
列方程:可用未知数,表示相等关系,依据是问题中的等量关系.在等式2.5x+318 =1068中,2.5,318,1068 叫做已知数,字母x表示的数,在解决这个问题之前还不知道,把它叫做未知数.我们把含有未知数的等式叫做方程.,2.4y + 2y + 2.4= 6.8也是方程。=把所要求的量用字母x(或y,···)表示,根据问题中的等量关系列出方程的过程,叫建立方程模型。问题3:
(1) 上述所列出的方程中含有几个未知数?是谁?
(2)含有未知数的项的次数是几?只含有一个未知数(元),含有未知数的项的次数都是1(次),这样的方程叫做一元一次方程.叫一元一次方程。能使方程左、右两边相等的未知数的值.叫方程的解。求方程的解的过程叫解方程。检验下列x的值是否是方程2.5x+318=1068的解
(1)x=300; (2)x=330.解:(1)把x=300代入原方程得,左边=
左边=右边,所以x=300是方程2.5x+318=1068的解(2)把x=330代入原方程得,左边=
左边 右边,所以x=330不是方程2.5x+318=1068的解2.5×330+318=11432.5×300+318=1068≠1.奥运村奠基仪式上种了一棵树,刚移栽时,树高为2m,假设以后平均每年长0.3m,几年后树高为5m?
设x年后树高为5m,可列出方程______________2.初一年级的女生占全年级学生数的52%,比全年级的男生多31人,初一年级共有多少学生?设初一年级共有学生x人,可列出方程 ______________3.根据下列问题,设未知数并列出方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?设边长为xcm设有x名学生1.判断下列方程是不是一元一次方程:(1)、(3)、(4)、(6)是一元一次方程.2.2008年北京奥运会的足球分赛场——秦皇岛市奥体中心体育场,其足球场的周长为344米,长和宽之差为36米,这个足球场的长与宽分别是多少米?请列出方程.解:设这个足球场的长为x米,则宽为(x-36)米.3.2008年北京奥运会志愿者报名中,某地区女士报名占该地区全部志愿者报名数的52%,比男士多80人,这个地区有多少志愿者报名?请列出方程.解:设这个地区有x名志愿者,则女士报名者有52%x人,男士报名者有(52%x-80)人.1枝钢笔比一枝铅笔多4元,应找你2元买4枝铅笔和一枝钢笔4、小英拿10元钱去买钢笔和铅笔。下面是小英与营业员的对话,你能根据她们的对话内容算出铅笔是多少钱1支吗?买4枝铅笔的钱+买一枝钢笔的钱=10-24x+(x+4)10-2=设1枝铅笔x元,得方程解例1 关于x的方程2(x-1)-a=0的解是3,则a的值是 ( ).
A.4 B.-4 C. 5 D.-5 本题中,应用方程的解的概念解题.把 x=3代入方程,得
2(3-1)-a=0
解之,得 a=4
故,应选择AA解例2 利用方程的定义对四个选项进行判断可知应选择D,因为D中不含未知数,它不符合方程的定义.
故,应选择D. 下列说法错误的是 ( ).
A. 3x-2x=5x是方程 B. x=0是方程
C. 2x-3y=1是方程 D. π=3.14是方程D问题1:这节课我们研究的主要内容是什么?问题2:用方程的方法来解决实际问题,一般要经历哪几个步骤?问题3:算术方法解题和用方程解题的区别是什么?(1)形式上,一个是算式,一个是含未知数的等式(方程);(2)列出的算式只能含有已知数,而方程中既含有已知数,又含有用字母表示的未知数;(3)思考问题的角度不同,前者是用已知数表示未知数,适用于关系简单的问题;后者重在寻找题中的等量关系,借助于字母表示未知数,列式表示等量关系.都是一种用于解决问题的工具. 根据下列问题,设未知数并列出方程1、 一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的修检时间2450小时?2、用一根长24cm的铁丝围成一个长方形,使它长是宽的1.5倍,长方形的长,宽各应是多少?3、某校女生占全体学生的52%,比男生多80人,这个学校有多少学生?4、一个梯形的下底比上底多2㎝,高是5㎝,面积是40㎝2,求上底.5、若方程是 一元一次方程,求m的值。 课外练习为下列各题建立一元一次方程:考考你1.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?
同课章节目录
