选择方案
图片预览




文档简介
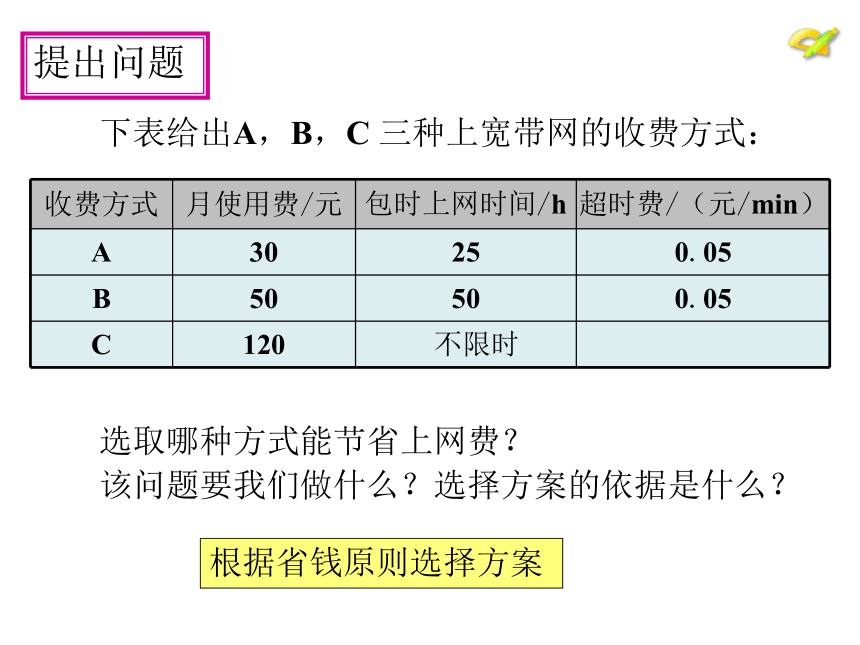
课件15张PPT。生活中的一次函数19.3 课题学习 选择方案 下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?根据省钱原则选择方案 提出问题分析问题方案A费用:方案B费用:方案C费用: y3=120. 请分别写出三种方案的上网费用y 元与上网时间t h
之间的函数解析式.
能把这个问题描述为函数问题吗?
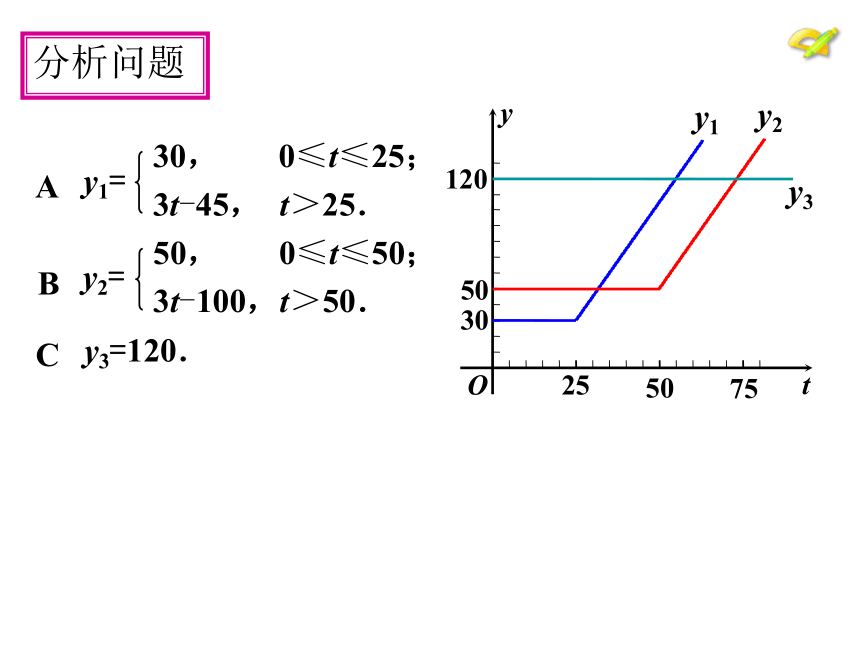
设上网时间为 t,方案A,B,C的上网费用分别为
y1 元,y2 元, y3 元,且分析问题请比较y1,y2,y3的大小. 这个问题看起来还是有点复杂,难点在于每一个函
数的解析都是分类表示的,需要分类讨论,而怎样分类
是难点.怎么办?
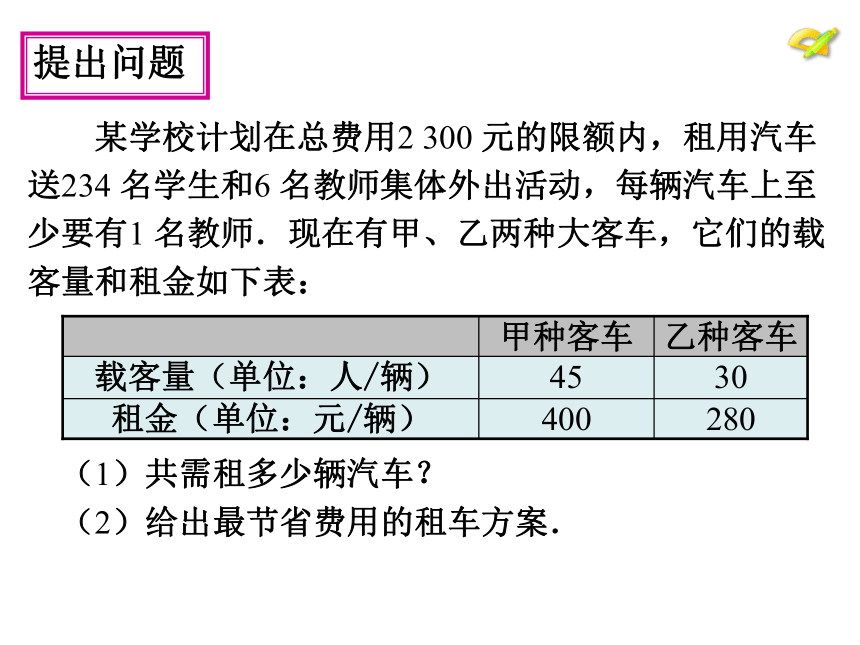
——先画出图象看看.y3=120. 分析问题 某学校计划在总费用2 300 元的限额内,租用汽车
送234 名学生和6 名教师集体外出活动,每辆汽车上至
少要有1 名教师.现在有甲、乙两种大客车,它们的载
客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.提出问题分析问题 问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 汽车所租辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数
不能大于6 辆.分析问题 问题4 在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为 y,则
y =400x+280(6-x)
化简 得
y =120x+1 680. 据实际意义可取4 或5;
因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最
小,y 的最小值为2 160.分析问题 (1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300. 问题5 如何确定 y =120x+1 680中 y 的最小值.从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,
乙地需水13万吨,A、B两水库各可调出水14万吨.从A地
到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙
地45千米.设计一个调运方案使水的调运量最小. 问题3 怎样调水所以,从A库往甲地调水1吨,从A库往乙地调水13吨,
从B库往甲地调水14吨,从B库往乙地调水0吨,可使水的调运量最小. 水量/万吨调入地调出地甲乙总计AB总计x14-x1415-xx-114151328设从A库往甲地调水X吨,总调运量为y. 则从A库往乙地调水(14-X)吨,从B库往甲地调水(15-X)吨,
从B库往乙地调水[13-(14-X)] = (x-1)吨。 y=50X+30(14-X)+60(15-X)+45(x-1)=1275+5X 因为X≤14,x-1≥0所以,1≤X≤14 当x=1时,y有最小值。 解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取有代表性的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型。
1、A地有机器16台,B地有机器12台,现要把化肥运往甲、乙
两地,现已知甲地需要15台,乙地需要13台。
如果从A地运往甲、乙两地运费分别是500元/台与400元/台,
从B地运往甲、乙两地运费分别是300元/台与600元/台,怎样调运花钱最少?X 台(16-X )台(15-X) 台〔12-(15-X)〕台整理得:y = 400x+9100 其中 0≤x ≤ 16设A地运往甲地x台,运输总费用为y,则:
y = ________________________________________500x+400(16-X )+300(15-X) +600(x-3)练一练2. A城有化肥200吨,B城有化肥300吨,现要把化肥运往C、D两农村,现已知C地需要240吨,D地需要260吨。
如果从A城运往C、D两地运费分别是20元/吨与25元/吨,
从B城运往C、D两地运费分别是15元/吨与24元吨,
怎样调运花钱最少?X 吨(200-X )吨(240-X) 吨〔300-(240-X)〕 吨解:设A城往C村的化肥有x吨,则往D村的有(200-X )吨,
B城往C村的有(240-X) 吨,剩余的〔300-(240-X)〕 吨运往D村;
若设总运费为y元,则 y =__________________________________________20x+25(200-X )+15 (240-X) +24(60+x)整理得:y = 4x+10040 其中 0≤x ≤ 200由于这个函数是个一次函数,且y随x的增大而增大,而x越小,y也越小,
所以当x=0时,y 最小,此时y=0+10040=10040因此,应由A城调往C村0吨,调往D村200吨,
再由B城调往C村240吨,调往D村60吨,3.某报亭从报社买进某种日报的价格是每份0.30元,
卖出的价格是每份0.50元,卖不出的报纸可以按每份0.10元
的价格退还给报社。经验表明,在一个月(30天)里,有20
天只能卖出150份报纸,其余10天每天可以卖出200份。设每
天从报社买进报纸的份数必须相同,那么这个报亭每天买进
多少份报纸才能使每月所获利润最大?最大利润是多少? ?
即y=-2x+1200(150≤x≤200).由于该函数在150≤x≤200时,y随x的增大而减小,
所以当x=150时,y有最大值,其最大值为:-2×150+1200=900(元)
?
解:设该报亭每天从报社买进报纸x份,所获月利润为y元。根据题意,得
?
y=(0.50-0.30)x·10+(0.50-0.30)×150×20 - (0.10-0.30)(x-150)×20.
?
(150≤x≤200)?? 答:报亭每天从报社买进150份报纸时,每月获得利润最大,最大利润为900元。4.某服装厂每天生产童装200套或西服50套,已知每生产一套童装需
成本40元,可获得利润22元;每生产一套西服需成本150元,可获
得利润80元;已知该厂每月成本支出不超过23万元,为使赢利尽量大,
若每月按30天计算,应安排生产童装和西服各多少天?(天数为整数),
z并求出最大利润。从而建立总利润模型为:22×200x+80×50(30—x),化简得400x+120000,
同时注意到每月成本支出不超过23万元,据此可得40×200x+150×50(30—x) ≤230000,从中求出x的取值限制为0≤x≤10,
且x为正整数,显然当x取10时赢利最大,最大利润为124000元。在运用一次函数知识和方法建模解决时,有时要涉及到多种方案,
通过比较,从中挑选出最佳的方案。200x50(30—x)40×200x150×50(30—x)22×200x80×50(30—x) 解:(1)设甲同学距学校的路程 ?s??(千米)与 t??(小时)
之间的函数关系式为s=k1x+b1 ,?由图可知,函数的图象经过点(1,0) 、
(0,25), 解得
???????????????????????
?
?????????????????????????? ????????????????? ?????????????????????????????? 设乙同学距学校的路程 s(千米)与t(小时)之间的函数关系式为 s=k2t+b2,由图可知,函数的图象经过点 (1.6,0) 、(0,20) ???????????????????????????? ?????? 解得 ???????????????????????? ????????????????????????????????? (2)由题意得, ?????????????????????????????????????????????,解得 ?????????????.
?
所以当行走了 ???????小时的时候,甲、乙两同学距学校的路程相等.
?
由图象知,当 ?????????????????????时,甲同学比乙同学离学校远.
?
当 ????????????????????????时,甲同学比乙同学离学校近.
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?根据省钱原则选择方案 提出问题分析问题方案A费用:方案B费用:方案C费用: y3=120. 请分别写出三种方案的上网费用y 元与上网时间t h
之间的函数解析式.
能把这个问题描述为函数问题吗?
设上网时间为 t,方案A,B,C的上网费用分别为
y1 元,y2 元, y3 元,且分析问题请比较y1,y2,y3的大小. 这个问题看起来还是有点复杂,难点在于每一个函
数的解析都是分类表示的,需要分类讨论,而怎样分类
是难点.怎么办?
——先画出图象看看.y3=120. 分析问题 某学校计划在总费用2 300 元的限额内,租用汽车
送234 名学生和6 名教师集体外出活动,每辆汽车上至
少要有1 名教师.现在有甲、乙两种大客车,它们的载
客量和租金如下表:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.提出问题分析问题 问题1 影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
问题2 汽车所租辆数又与哪些因素有关?
与乘车人数有关.
问题3 如何由乘车人数确定租车辆数呢?
(1)要保证240 名师生都有车坐,汽车总数不能小于6 辆;
(2)要使每辆汽车上至少有1 名教师,汽车总数
不能大于6 辆.分析问题 问题4 在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x 辆,能求出租车费用吗?
设租用 x 辆甲种客车,则租用乙种客车的辆数为
(6-x)辆;设租车费用为 y,则
y =400x+280(6-x)
化简 得
y =120x+1 680. 据实际意义可取4 或5;
因为 y 随着 x 的增大而增大,所以当 x =4 时,y 最
小,y 的最小值为2 160.分析问题 (1)为使240 名师生有车坐,则
45x+30(6-x)≥240;
(2)为使租车费用不超过2 300 元,则
400x+280(6-x)≤2 300. 问题5 如何确定 y =120x+1 680中 y 的最小值.从A、B两水库向甲、乙两地调水,其中甲地需水15万吨,
乙地需水13万吨,A、B两水库各可调出水14万吨.从A地
到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙
地45千米.设计一个调运方案使水的调运量最小. 问题3 怎样调水所以,从A库往甲地调水1吨,从A库往乙地调水13吨,
从B库往甲地调水14吨,从B库往乙地调水0吨,可使水的调运量最小. 水量/万吨调入地调出地甲乙总计AB总计x14-x1415-xx-114151328设从A库往甲地调水X吨,总调运量为y. 则从A库往乙地调水(14-X)吨,从B库往甲地调水(15-X)吨,
从B库往乙地调水[13-(14-X)] = (x-1)吨。 y=50X+30(14-X)+60(15-X)+45(x-1)=1275+5X 因为X≤14,x-1≥0所以,1≤X≤14 当x=1时,y有最小值。 解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取有代表性的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型。
1、A地有机器16台,B地有机器12台,现要把化肥运往甲、乙
两地,现已知甲地需要15台,乙地需要13台。
如果从A地运往甲、乙两地运费分别是500元/台与400元/台,
从B地运往甲、乙两地运费分别是300元/台与600元/台,怎样调运花钱最少?X 台(16-X )台(15-X) 台〔12-(15-X)〕台整理得:y = 400x+9100 其中 0≤x ≤ 16设A地运往甲地x台,运输总费用为y,则:
y = ________________________________________500x+400(16-X )+300(15-X) +600(x-3)练一练2. A城有化肥200吨,B城有化肥300吨,现要把化肥运往C、D两农村,现已知C地需要240吨,D地需要260吨。
如果从A城运往C、D两地运费分别是20元/吨与25元/吨,
从B城运往C、D两地运费分别是15元/吨与24元吨,
怎样调运花钱最少?X 吨(200-X )吨(240-X) 吨〔300-(240-X)〕 吨解:设A城往C村的化肥有x吨,则往D村的有(200-X )吨,
B城往C村的有(240-X) 吨,剩余的〔300-(240-X)〕 吨运往D村;
若设总运费为y元,则 y =__________________________________________20x+25(200-X )+15 (240-X) +24(60+x)整理得:y = 4x+10040 其中 0≤x ≤ 200由于这个函数是个一次函数,且y随x的增大而增大,而x越小,y也越小,
所以当x=0时,y 最小,此时y=0+10040=10040因此,应由A城调往C村0吨,调往D村200吨,
再由B城调往C村240吨,调往D村60吨,3.某报亭从报社买进某种日报的价格是每份0.30元,
卖出的价格是每份0.50元,卖不出的报纸可以按每份0.10元
的价格退还给报社。经验表明,在一个月(30天)里,有20
天只能卖出150份报纸,其余10天每天可以卖出200份。设每
天从报社买进报纸的份数必须相同,那么这个报亭每天买进
多少份报纸才能使每月所获利润最大?最大利润是多少? ?
即y=-2x+1200(150≤x≤200).由于该函数在150≤x≤200时,y随x的增大而减小,
所以当x=150时,y有最大值,其最大值为:-2×150+1200=900(元)
?
解:设该报亭每天从报社买进报纸x份,所获月利润为y元。根据题意,得
?
y=(0.50-0.30)x·10+(0.50-0.30)×150×20 - (0.10-0.30)(x-150)×20.
?
(150≤x≤200)?? 答:报亭每天从报社买进150份报纸时,每月获得利润最大,最大利润为900元。4.某服装厂每天生产童装200套或西服50套,已知每生产一套童装需
成本40元,可获得利润22元;每生产一套西服需成本150元,可获
得利润80元;已知该厂每月成本支出不超过23万元,为使赢利尽量大,
若每月按30天计算,应安排生产童装和西服各多少天?(天数为整数),
z并求出最大利润。从而建立总利润模型为:22×200x+80×50(30—x),化简得400x+120000,
同时注意到每月成本支出不超过23万元,据此可得40×200x+150×50(30—x) ≤230000,从中求出x的取值限制为0≤x≤10,
且x为正整数,显然当x取10时赢利最大,最大利润为124000元。在运用一次函数知识和方法建模解决时,有时要涉及到多种方案,
通过比较,从中挑选出最佳的方案。200x50(30—x)40×200x150×50(30—x)22×200x80×50(30—x) 解:(1)设甲同学距学校的路程 ?s??(千米)与 t??(小时)
之间的函数关系式为s=k1x+b1 ,?由图可知,函数的图象经过点(1,0) 、
(0,25), 解得
???????????????????????
?
?????????????????????????? ????????????????? ?????????????????????????????? 设乙同学距学校的路程 s(千米)与t(小时)之间的函数关系式为 s=k2t+b2,由图可知,函数的图象经过点 (1.6,0) 、(0,20) ???????????????????????????? ?????? 解得 ???????????????????????? ????????????????????????????????? (2)由题意得, ?????????????????????????????????????????????,解得 ?????????????.
?
所以当行走了 ???????小时的时候,甲、乙两同学距学校的路程相等.
?
由图象知,当 ?????????????????????时,甲同学比乙同学离学校远.
?
当 ????????????????????????时,甲同学比乙同学离学校近.
