4.1认识三角形(第一课时) 课件(16张PPT)
文档属性
| 名称 | 4.1认识三角形(第一课时) 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第四章 三角形
4.1 认识三角形
第一课时 三角形及其内角和
学习目标
1)了解三角形及其相关概念,能正确识别和表示三角形。
2)利用角的大小对三角形进行分类。
3)探索并推导三角形的内角和等于180°。
重点
利用角的大小对三角形进行分类。
难点
根据三角形内角和等于180°进行简单计算。
三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形。
A
B
C
【思考】判断下列图形是三角形吗,并说明原因?
不是,首尾无顺次相接
不是,首尾无顺次相接
不是,三条线段在同一条直线上
组成三角形的三条线段叫做三角形的边。
三角形相邻两边的公共端点叫做三角形的顶点。
三角形相邻两边所组成的角叫做三角形的内角。简称三角形的角。∠B,C)
A
B
C
角
角
角
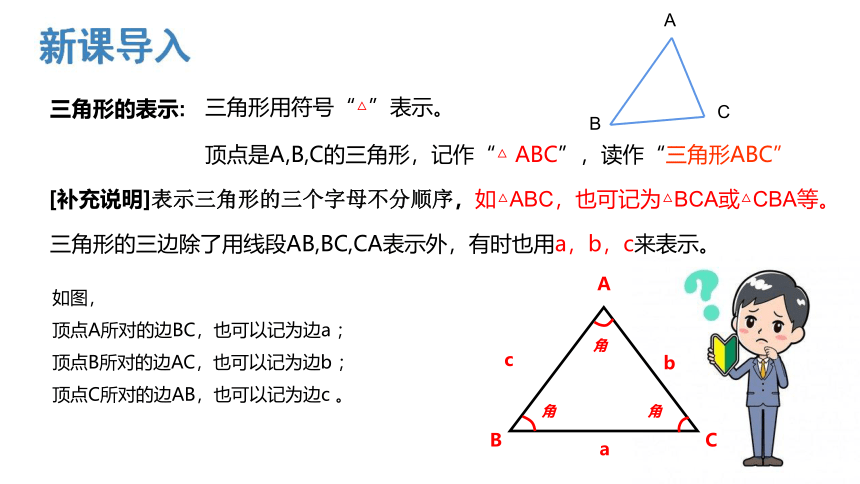
三角形用符号“△”表示。
顶点是A,B,C的三角形,记作“△ ABC”,读作“三角形ABC”
[补充说明]表示三角形的三个字母不分顺序,如△ABC,也可记为△BCA或△CBA等。
三角形的表示:
A
B
C
c
b
a
A
B
C
角
角
角
三角形的三边除了用线段AB,BC,CA表示外,有时也用a,b,c来表示。
如图,
顶点A所对的边BC,也可以记为边a ;
顶点B所对的边AC,也可以记为边b ;
顶点C所对的边AB,也可以记为边c 。
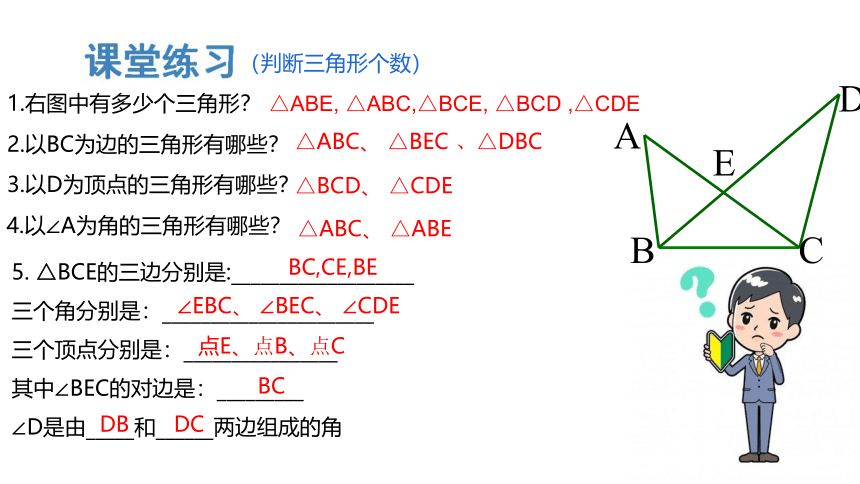
(判断三角形个数)
A
D
C
B
E
2.以BC为边的三角形有哪些?
△ABC、 △BEC 、△DBC
3.以D为顶点的三角形有哪些?
△BCD、 △CDE
4.以∠A为角的三角形有哪些?
△ABC、 △ABE
1.右图中有多少个三角形?
△ABE, △ABC,△BCE, △BCD ,△CDE
5. △BCE的三边分别是:___________________
三个角分别是:______________________
三个顶点分别是:________________
其中∠BEC的对边是:_________
∠D是由_____和______两边组成的角
BC,CE,BE
∠EBC、 ∠BEC、 ∠CDE
点E、点B、点C
BC
DB
DC
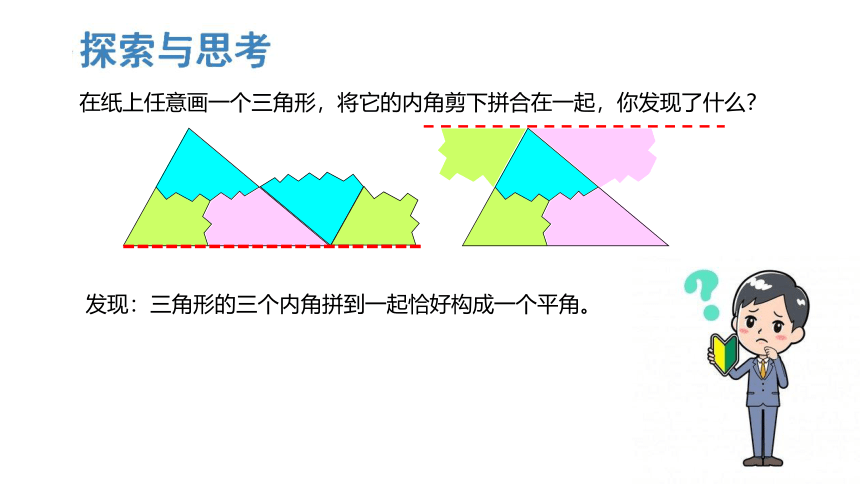
发现:三角形的三个内角拼到一起恰好构成一个平角。
在纸上任意画一个三角形,将它的内角剪下拼合在一起,你发现了什么?
A
B
C
1
2
3
4
5
L
证明:过点A 做BC边平行线L,使L∥BC
∵ L∥BC
∴ ∠1= ∠4, ∠3= ∠5
∵ ∠1, ∠2, ∠3组成平角
∴ ∠1+∠2+∠3=180°
则∠2+∠4+∠5=180°
三角形内角和等于180°
已知△ABC,求证:∠A+∠B+∠C=180°
(利用三角形内角和进行有关计算)
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:∵在△ABC中,∠A=80°
而∠A+∠B+∠C=180°,
∴∠B+∠C=100°
而∠B=∠C
∴∠B=∠C=500
A
B
C
(利用三角形内角和进行有关计算)
已知三角形三个内角的度数之比为2:3:7,求这三个内角的度数。
解:设三个内角度数分别为:2x、3x、7x,
由三角形内角和为180°,得:2x+3x+7x=180° 解得x=15
所以三个内角度数分别为30°,45°,105°。
(利用三角形内角和进行有关计算)
如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=75°,则∠B的数为( )
A.25° B.30° C.40° D.50°
【详解】
解:∵CD=CE,∴∠D=∠CED=75°,
∴∠DCB=180°-∠D-∠CED =180°-75°-75°=30°,
∵CD∥AB,∴∠B=∠C=30°,
故选:B.
(利用三角形内角和进行有关计算)
在中,,,如果平分,那么的度数是( )
A. B. C. D.
【详解】
解:
平分,
故选C.
在直角三角形ABC中,∠C=90°
∵∠ A+∠ B+∠C=180° 而∠C=90°,
∴∠ A+∠ B=90°
直角三角形的两个锐角互余
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC
三角形
锐角三角形
三个都是锐角
直角三角形
一个直角+两个锐角
钝角三角形
一个钝角+两个锐角
构成
(1)一个三角形中最多有_____个直角?为什么?
(2)一个三角形中最多有_____个钝角?为什么?
(3)一个三角形中至少有_____个锐角?为什么?
(4)任意一个三角形中,最大的一个角的度数至少为________.
60°
2
1
1
三角形
三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
三角形按角分类
直角三角形
锐角三角形
钝角三角形
三角形的内角和等于180°
直角三角形的两个锐角互余
第四章 三角形
4.1 认识三角形
第一课时 三角形及其内角和
学习目标
1)了解三角形及其相关概念,能正确识别和表示三角形。
2)利用角的大小对三角形进行分类。
3)探索并推导三角形的内角和等于180°。
重点
利用角的大小对三角形进行分类。
难点
根据三角形内角和等于180°进行简单计算。
三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形。
A
B
C
【思考】判断下列图形是三角形吗,并说明原因?
不是,首尾无顺次相接
不是,首尾无顺次相接
不是,三条线段在同一条直线上
组成三角形的三条线段叫做三角形的边。
三角形相邻两边的公共端点叫做三角形的顶点。
三角形相邻两边所组成的角叫做三角形的内角。简称三角形的角。∠B,C)
A
B
C
角
角
角
三角形用符号“△”表示。
顶点是A,B,C的三角形,记作“△ ABC”,读作“三角形ABC”
[补充说明]表示三角形的三个字母不分顺序,如△ABC,也可记为△BCA或△CBA等。
三角形的表示:
A
B
C
c
b
a
A
B
C
角
角
角
三角形的三边除了用线段AB,BC,CA表示外,有时也用a,b,c来表示。
如图,
顶点A所对的边BC,也可以记为边a ;
顶点B所对的边AC,也可以记为边b ;
顶点C所对的边AB,也可以记为边c 。
(判断三角形个数)
A
D
C
B
E
2.以BC为边的三角形有哪些?
△ABC、 △BEC 、△DBC
3.以D为顶点的三角形有哪些?
△BCD、 △CDE
4.以∠A为角的三角形有哪些?
△ABC、 △ABE
1.右图中有多少个三角形?
△ABE, △ABC,△BCE, △BCD ,△CDE
5. △BCE的三边分别是:___________________
三个角分别是:______________________
三个顶点分别是:________________
其中∠BEC的对边是:_________
∠D是由_____和______两边组成的角
BC,CE,BE
∠EBC、 ∠BEC、 ∠CDE
点E、点B、点C
BC
DB
DC
发现:三角形的三个内角拼到一起恰好构成一个平角。
在纸上任意画一个三角形,将它的内角剪下拼合在一起,你发现了什么?
A
B
C
1
2
3
4
5
L
证明:过点A 做BC边平行线L,使L∥BC
∵ L∥BC
∴ ∠1= ∠4, ∠3= ∠5
∵ ∠1, ∠2, ∠3组成平角
∴ ∠1+∠2+∠3=180°
则∠2+∠4+∠5=180°
三角形内角和等于180°
已知△ABC,求证:∠A+∠B+∠C=180°
(利用三角形内角和进行有关计算)
在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:∵在△ABC中,∠A=80°
而∠A+∠B+∠C=180°,
∴∠B+∠C=100°
而∠B=∠C
∴∠B=∠C=500
A
B
C
(利用三角形内角和进行有关计算)
已知三角形三个内角的度数之比为2:3:7,求这三个内角的度数。
解:设三个内角度数分别为:2x、3x、7x,
由三角形内角和为180°,得:2x+3x+7x=180° 解得x=15
所以三个内角度数分别为30°,45°,105°。
(利用三角形内角和进行有关计算)
如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=75°,则∠B的数为( )
A.25° B.30° C.40° D.50°
【详解】
解:∵CD=CE,∴∠D=∠CED=75°,
∴∠DCB=180°-∠D-∠CED =180°-75°-75°=30°,
∵CD∥AB,∴∠B=∠C=30°,
故选:B.
(利用三角形内角和进行有关计算)
在中,,,如果平分,那么的度数是( )
A. B. C. D.
【详解】
解:
平分,
故选C.
在直角三角形ABC中,∠C=90°
∵∠ A+∠ B+∠C=180° 而∠C=90°,
∴∠ A+∠ B=90°
直角三角形的两个锐角互余
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC
三角形
锐角三角形
三个都是锐角
直角三角形
一个直角+两个锐角
钝角三角形
一个钝角+两个锐角
构成
(1)一个三角形中最多有_____个直角?为什么?
(2)一个三角形中最多有_____个钝角?为什么?
(3)一个三角形中至少有_____个锐角?为什么?
(4)任意一个三角形中,最大的一个角的度数至少为________.
60°
2
1
1
三角形
三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.
三角形按角分类
直角三角形
锐角三角形
钝角三角形
三角形的内角和等于180°
直角三角形的两个锐角互余
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
