18.1平行四边形的性质课件(共38张PPT)2022—2023学年华东师大版数学八年级下册
文档属性
| 名称 | 18.1平行四边形的性质课件(共38张PPT)2022—2023学年华东师大版数学八年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 19:49:42 | ||
图片预览










文档简介
(共38张PPT)
18.1 平行四边形的性质
第18章 平行四边形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
平行四边形
平行四边形的边、角性质
两条平行线之间的距离
平行四边形的对角线性质
知识点
感悟新知
1
平行四边形
1. 定义:两组对边分别平行的四边形叫做平行四边形.
特别提醒
●平行四边形的定义有两个要素:
(1)是四边形;
(2)两组对边分别平行.作为四边形,平行四边形具有一般四边形的一切性质.
●平行四边形的定义既是它的一个性质,又是它的一种判定方法:∵四边形ABCD是平行四边形,∴ AB∥CD,AD∥BC;
反过来,∵ AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.
感悟新知
2. 表示方法:平行四边形用符号“ ”表示,如图18.1-1,平行四边形ABCD 记作“ ABCD”,读作“平行四边形ABCD”.
感悟新知
注意:
(1)平行四边形的表示一定要按顺时针或逆时针依次注明各顶点,不能打乱顺序.
(2)“ ”作为表示平行四边形的符号,不可单独使用它来代替“平行四边形”.
感悟新知
3. 平行四边形的基本元素:
基本元素 主要内容 图示
边 邻边 AD 和AB,AD 和DC,DC 和BC,BC 和AB,共有四对
对边 AB 和DC,AD 和BC,共有两对
角 邻角 ∠ BAD 和∠ ADC,∠ ADC 和∠ DCB,∠ DCB 和∠ ABC,∠ DAB 和∠ ABC,共有四对
对角 ∠ BAD 和∠ BCD,∠ ADC 和∠ ABC,共有两对
对角线 AC 和BD,共有两条
感悟新知
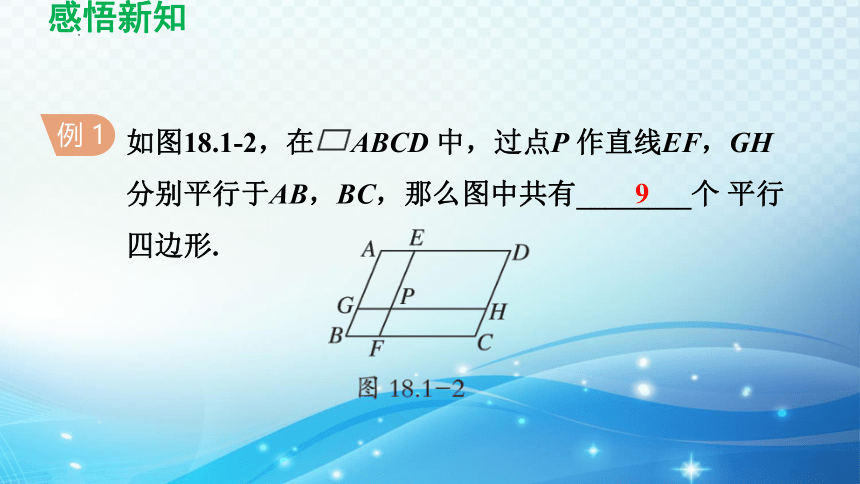
如图18.1-2,在 ABCD 中,过点P 作直线EF,GH分别平行于AB,BC,那么图中共有________个 平行四边形.
例 1
9
感悟新知
解题秘方:紧扣平行四边形定义中的“两要素”进行识别.
感悟新知
解:在 ABCD 中,∵ EF ∥ AB,GH ∥ BC,
∴ EF ∥ AB ∥ CD,GH ∥ BC ∥ AD.
∴单独一个四边形是平行四边形的有4 个:
DEPH, EAGP, HPFC, PGBF;
由两个四边形组成的平行四边形有4 个:
DEFC, EABF, DAGH, HGBC;
由四个四边形组成的平行四边形有1 个: ABCD.
∴图中共有9 个平行四边形.
感悟新知
1-1. 如图, 分别过△ ABC 的顶点A,B,C 作对边BC,AC,AB的平行线,交点分别为E,F,D. 请找出图中所有的平行四边形,并表示出来.
解:平行四边形有 ABCD, AEBC, ABFC.
知识点
平行四边形的边、角性质
感悟新知
2
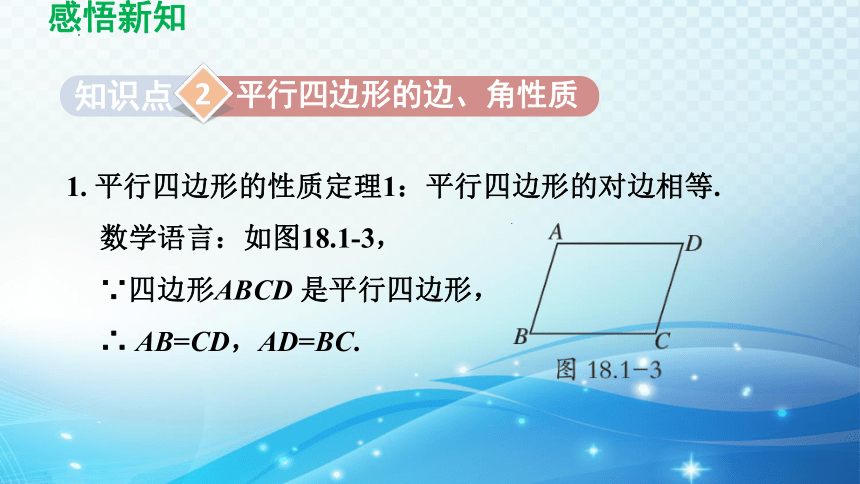
1. 平行四边形的性质定理1:平行四边形的对边相等.
数学语言:如图18.1-3,
∵四边形ABCD 是平行四边形,
∴ AB=CD,AD=BC.
感悟新知
2. 平行四边形的性质定理2:平行四边形的对角相等.
数学语言:如图18.1-3,
∵四边形ABCD 是平行四边形,
∴∠ A= ∠ C,∠ B= ∠ D.
感悟新知
特别提醒
由于组成平行四边形的元素有边和角,因此讨论其性质也应从边和角这两个方面去看.
(1)从边看:平行四边形的对边平行且相等;
(2)从角看:平行四边形的对角相等、邻角互补.
感悟新知
如图18.1-4,在ABCD 中,AB=5 cm,BC=4 cm,
则ABCD 的周长为 ________cm.
例2
解题秘方:紧扣“平行四边形边的性质”进行解答.
18
感悟新知
解:∵平行四边形的对边相等,
∴ CD=AB=5 cm,AD=BC=4 cm.
∴ ABCD 的周长=AB+BC+CD+AD=5+4+5+4=18(cm).
感悟新知
2-1. [中考·湘潭]如图,在ABCD 中,连结AC,已知∠ BAC=40°,∠ ACB=80°,则∠ BCD=( )
A. 80°
B. 100°
C. 120°
D. 140°
C
知识点
两条平行线之间的距离
感悟新知
3
1. 定义:两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
特别提醒
1. 距离是指垂线段的长度,它是正值;
2. 当两条平行线确定后,它们之间的距离是一个定值,不随位置的不同而改变;
3. 平行线间的距离处处相等,因此在作平行四边形的高时,可根据需要灵活选择位置;
4. 任何两条平行线间的距离都是存在的、唯一的,都是两条平行线间最短线段的长度.
感悟新知
三种距离之间的区别与联系
类别 两点间的距离 点到直线的距离 两条平行线间的距离
区别 连结两点的线段的长度 点到直线的垂线段的长度 两条平行线中,一条直线上任意一点到另一条直线的垂线段的长度
联系 最后都归结为两点间的一条线段的长度
感悟新知
2. 性质:平行线之间的距离处处相等.
3. 拓展:(1)夹在两条平行线间的任何
平行线段都相等.
(2)等底等高的平行四边形的面积相等.
(3)平行四边形的面积= 底× 高=ah(其中a 是平行四边形的任意一条边长,h 必须是边长为a 的边与它的对边之间的距离). 如图18.1- 5,在 ABCD 中,AE ⊥ BC 于点E,CF ⊥ AB 于点F,则S ABCD=BC·AE=AB·CF.
感悟新知
如图18.1-6,直线a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF.△ABC与△DEF的面积相等吗?为什么?
解题秘方:紧扣等底等高的三角形面积相等作三角形的高进行说明.
例 3
感悟新知
解:△ ABC 与△ DEF 的面积相等.
理由如下:如图18.1-6,过点A 作AH1 ⊥
直线b,垂足为点H1,
过点D 作DH2 ⊥直线a,垂足为点H2.
设△ ABC 和△ DEF 的面积分别为S1 和S2,
∴ S1= BC·AH1,S2= EF·DH2.
感悟新知
∵直线a ∥ b,AH1 ⊥直线b,DH2 ⊥直线a,
∴ AH1=DH2.
又∵ BC=EF,∴ S1=S2,
即△ ABC 与△ DEF 的面积相等.
感悟新知
3-1.[中考·青海]如图,在 ABCD 中,对角线BD=
8 cm,AE ⊥BD,垂足为E,且AE=3 cm,BC=4 cm, 则AD 与BC 之间的距离为_______.
6 cm
知识点
平行四边形的对角线性质
感悟新知
4
1. 平行四边形的性质定理3:平行四边形的对角线互相平分.
数学语言:如图18.1-7,
∵四边形ABCD 是平行四边形,
∴ OA=OC= AC,OB=OD= BD.
感悟新知
2. 拓展性质:
(1)平行四边形的一条对角线将平行四边形分成面积相等的两部分,两条对角线将平行四边形分成面积相等的四部分.
(2)若一条直线过平行四边形两条对角线的交点,则该直线平分平行四边形的周长和面积.
感悟新知
图示
如图18.1-8,∵直线EF 过平行四边形ABCD对角线的交点O,∴△ AOE ≌△ COF,△ DOE ≌△ BOF.∴易得直线EF 平分 ABCD的周长和面积.
感悟新知
如图18.1-9,已知ABCD 的周长是60,对角线AC,
BD 相交于点O. 若△ AOB 的周长比△ BOC 的周长长8,求这个平行四边形各边的长.
例4
周长之差转化为邻边之差.
解题秘方:紧扣平行四边形对角线、边的性质进行解答.
感悟新知
解:∵四边形ABCD 是平行四边形,
∴ OA=OC,AB=CD,AD=BC.
∵ AB+BC+CD+DA=60,
OA+AB+OB-(OB+BC+OC)=8,
∴ AB+BC=30,AB-BC=8. ∴ AB=19,BC=11.
∴ CD=19,AD=11.
∴这个平行四边形各边的长分别为19,11,19,11.
感悟新知
4-1. 如图, ABCD的对角线交于点O,且AC ⊥ AB,OC=1 cm,OB=2 cm. 求AB 的长及 ABCD 的面积.
感悟新知
感悟新知
如图18.1-10,在 ABCD中,对角线AC,BD 相交于点O,过点O 作直线EF,分别交AD,BC 于点E,
F. 判断四边形ABFE 的面积与四边形FCDE的面积有何关系?试说明理由.
解题秘方:紧扣平行四边形的对角线性质、全等三角形的性质进行解答.
例 5
感悟新知
解:S四边形ABFE=S四边形FCDE.
理由如下:∵四边形ABCD 是平行四边形,
∴ OA=OC,AD ∥ BC.∴∠ 1= ∠ 2.
又∵∠ 3= ∠ 4,∴△ AOE ≌△ COF(A. S. A.).
∴ S△ AOE=S△ COF.
∴ S四边形ABFE=S△ ABC-S△ COF+S△ AOE=S△ ABC,
S四边形FCDE=S△ CDA-S△ AOE+S△ COF=S△ CDA,
感悟新知
∵在 ABCD 中,AB=CD,
BC=DA,∠ ABC= ∠ CDA,
∴△ ABC ≌△ CDA(S. A. S.).
∴ S△ ABC=S△ CDA.
∴ S四边形ABFE=S四边形FCDE.
感悟新知
5-1. 张大伯承包了一个四边形的池塘,如图所示,它的四个顶点A,B,C,D 处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且要使扩建后的池塘呈平行四边形形状. 张大伯这一设想是
否能实现?请你帮助他解决
一下,并画出草图.
感悟新知
解:张大伯能实现这一设想.有多种设计方案,现列举两种如下:
方案一:如图①,连结AC.过点D作DH∥AC,且使DH=AC,连结HA,过点B作AC的平行线,延长HA,DC,分别交过点B且平行于AC的直线于点E,F,则四边形EFDH即为扩建后的平行四边形池塘.
感悟新知
方案二:如图②,连结AC,BD.分别过点B,D作AC的平行线,分别过点A,C作BD的平行线,这两组平行线的交点分别为点E,F,G,H,则四边形EFGH即为扩建后的平行四边形池塘.(设计方案不唯一)
本节小结
平行四边形的性质
平行四边形
定义
表示方法
性质
平行线间的距离
请完成教材课后习题
作业提升
18.1 平行四边形的性质
第18章 平行四边形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
平行四边形
平行四边形的边、角性质
两条平行线之间的距离
平行四边形的对角线性质
知识点
感悟新知
1
平行四边形
1. 定义:两组对边分别平行的四边形叫做平行四边形.
特别提醒
●平行四边形的定义有两个要素:
(1)是四边形;
(2)两组对边分别平行.作为四边形,平行四边形具有一般四边形的一切性质.
●平行四边形的定义既是它的一个性质,又是它的一种判定方法:∵四边形ABCD是平行四边形,∴ AB∥CD,AD∥BC;
反过来,∵ AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.
感悟新知
2. 表示方法:平行四边形用符号“ ”表示,如图18.1-1,平行四边形ABCD 记作“ ABCD”,读作“平行四边形ABCD”.
感悟新知
注意:
(1)平行四边形的表示一定要按顺时针或逆时针依次注明各顶点,不能打乱顺序.
(2)“ ”作为表示平行四边形的符号,不可单独使用它来代替“平行四边形”.
感悟新知
3. 平行四边形的基本元素:
基本元素 主要内容 图示
边 邻边 AD 和AB,AD 和DC,DC 和BC,BC 和AB,共有四对
对边 AB 和DC,AD 和BC,共有两对
角 邻角 ∠ BAD 和∠ ADC,∠ ADC 和∠ DCB,∠ DCB 和∠ ABC,∠ DAB 和∠ ABC,共有四对
对角 ∠ BAD 和∠ BCD,∠ ADC 和∠ ABC,共有两对
对角线 AC 和BD,共有两条
感悟新知
如图18.1-2,在 ABCD 中,过点P 作直线EF,GH分别平行于AB,BC,那么图中共有________个 平行四边形.
例 1
9
感悟新知
解题秘方:紧扣平行四边形定义中的“两要素”进行识别.
感悟新知
解:在 ABCD 中,∵ EF ∥ AB,GH ∥ BC,
∴ EF ∥ AB ∥ CD,GH ∥ BC ∥ AD.
∴单独一个四边形是平行四边形的有4 个:
DEPH, EAGP, HPFC, PGBF;
由两个四边形组成的平行四边形有4 个:
DEFC, EABF, DAGH, HGBC;
由四个四边形组成的平行四边形有1 个: ABCD.
∴图中共有9 个平行四边形.
感悟新知
1-1. 如图, 分别过△ ABC 的顶点A,B,C 作对边BC,AC,AB的平行线,交点分别为E,F,D. 请找出图中所有的平行四边形,并表示出来.
解:平行四边形有 ABCD, AEBC, ABFC.
知识点
平行四边形的边、角性质
感悟新知
2
1. 平行四边形的性质定理1:平行四边形的对边相等.
数学语言:如图18.1-3,
∵四边形ABCD 是平行四边形,
∴ AB=CD,AD=BC.
感悟新知
2. 平行四边形的性质定理2:平行四边形的对角相等.
数学语言:如图18.1-3,
∵四边形ABCD 是平行四边形,
∴∠ A= ∠ C,∠ B= ∠ D.
感悟新知
特别提醒
由于组成平行四边形的元素有边和角,因此讨论其性质也应从边和角这两个方面去看.
(1)从边看:平行四边形的对边平行且相等;
(2)从角看:平行四边形的对角相等、邻角互补.
感悟新知
如图18.1-4,在ABCD 中,AB=5 cm,BC=4 cm,
则ABCD 的周长为 ________cm.
例2
解题秘方:紧扣“平行四边形边的性质”进行解答.
18
感悟新知
解:∵平行四边形的对边相等,
∴ CD=AB=5 cm,AD=BC=4 cm.
∴ ABCD 的周长=AB+BC+CD+AD=5+4+5+4=18(cm).
感悟新知
2-1. [中考·湘潭]如图,在ABCD 中,连结AC,已知∠ BAC=40°,∠ ACB=80°,则∠ BCD=( )
A. 80°
B. 100°
C. 120°
D. 140°
C
知识点
两条平行线之间的距离
感悟新知
3
1. 定义:两条直线平行,其中一条直线上的任一点到另一条直线的距离,叫做这两条平行线之间的距离.
特别提醒
1. 距离是指垂线段的长度,它是正值;
2. 当两条平行线确定后,它们之间的距离是一个定值,不随位置的不同而改变;
3. 平行线间的距离处处相等,因此在作平行四边形的高时,可根据需要灵活选择位置;
4. 任何两条平行线间的距离都是存在的、唯一的,都是两条平行线间最短线段的长度.
感悟新知
三种距离之间的区别与联系
类别 两点间的距离 点到直线的距离 两条平行线间的距离
区别 连结两点的线段的长度 点到直线的垂线段的长度 两条平行线中,一条直线上任意一点到另一条直线的垂线段的长度
联系 最后都归结为两点间的一条线段的长度
感悟新知
2. 性质:平行线之间的距离处处相等.
3. 拓展:(1)夹在两条平行线间的任何
平行线段都相等.
(2)等底等高的平行四边形的面积相等.
(3)平行四边形的面积= 底× 高=ah(其中a 是平行四边形的任意一条边长,h 必须是边长为a 的边与它的对边之间的距离). 如图18.1- 5,在 ABCD 中,AE ⊥ BC 于点E,CF ⊥ AB 于点F,则S ABCD=BC·AE=AB·CF.
感悟新知
如图18.1-6,直线a∥b,点A,E,F在直线a上,点B,C,D在直线b上,BC=EF.△ABC与△DEF的面积相等吗?为什么?
解题秘方:紧扣等底等高的三角形面积相等作三角形的高进行说明.
例 3
感悟新知
解:△ ABC 与△ DEF 的面积相等.
理由如下:如图18.1-6,过点A 作AH1 ⊥
直线b,垂足为点H1,
过点D 作DH2 ⊥直线a,垂足为点H2.
设△ ABC 和△ DEF 的面积分别为S1 和S2,
∴ S1= BC·AH1,S2= EF·DH2.
感悟新知
∵直线a ∥ b,AH1 ⊥直线b,DH2 ⊥直线a,
∴ AH1=DH2.
又∵ BC=EF,∴ S1=S2,
即△ ABC 与△ DEF 的面积相等.
感悟新知
3-1.[中考·青海]如图,在 ABCD 中,对角线BD=
8 cm,AE ⊥BD,垂足为E,且AE=3 cm,BC=4 cm, 则AD 与BC 之间的距离为_______.
6 cm
知识点
平行四边形的对角线性质
感悟新知
4
1. 平行四边形的性质定理3:平行四边形的对角线互相平分.
数学语言:如图18.1-7,
∵四边形ABCD 是平行四边形,
∴ OA=OC= AC,OB=OD= BD.
感悟新知
2. 拓展性质:
(1)平行四边形的一条对角线将平行四边形分成面积相等的两部分,两条对角线将平行四边形分成面积相等的四部分.
(2)若一条直线过平行四边形两条对角线的交点,则该直线平分平行四边形的周长和面积.
感悟新知
图示
如图18.1-8,∵直线EF 过平行四边形ABCD对角线的交点O,∴△ AOE ≌△ COF,△ DOE ≌△ BOF.∴易得直线EF 平分 ABCD的周长和面积.
感悟新知
如图18.1-9,已知ABCD 的周长是60,对角线AC,
BD 相交于点O. 若△ AOB 的周长比△ BOC 的周长长8,求这个平行四边形各边的长.
例4
周长之差转化为邻边之差.
解题秘方:紧扣平行四边形对角线、边的性质进行解答.
感悟新知
解:∵四边形ABCD 是平行四边形,
∴ OA=OC,AB=CD,AD=BC.
∵ AB+BC+CD+DA=60,
OA+AB+OB-(OB+BC+OC)=8,
∴ AB+BC=30,AB-BC=8. ∴ AB=19,BC=11.
∴ CD=19,AD=11.
∴这个平行四边形各边的长分别为19,11,19,11.
感悟新知
4-1. 如图, ABCD的对角线交于点O,且AC ⊥ AB,OC=1 cm,OB=2 cm. 求AB 的长及 ABCD 的面积.
感悟新知
感悟新知
如图18.1-10,在 ABCD中,对角线AC,BD 相交于点O,过点O 作直线EF,分别交AD,BC 于点E,
F. 判断四边形ABFE 的面积与四边形FCDE的面积有何关系?试说明理由.
解题秘方:紧扣平行四边形的对角线性质、全等三角形的性质进行解答.
例 5
感悟新知
解:S四边形ABFE=S四边形FCDE.
理由如下:∵四边形ABCD 是平行四边形,
∴ OA=OC,AD ∥ BC.∴∠ 1= ∠ 2.
又∵∠ 3= ∠ 4,∴△ AOE ≌△ COF(A. S. A.).
∴ S△ AOE=S△ COF.
∴ S四边形ABFE=S△ ABC-S△ COF+S△ AOE=S△ ABC,
S四边形FCDE=S△ CDA-S△ AOE+S△ COF=S△ CDA,
感悟新知
∵在 ABCD 中,AB=CD,
BC=DA,∠ ABC= ∠ CDA,
∴△ ABC ≌△ CDA(S. A. S.).
∴ S△ ABC=S△ CDA.
∴ S四边形ABFE=S四边形FCDE.
感悟新知
5-1. 张大伯承包了一个四边形的池塘,如图所示,它的四个顶点A,B,C,D 处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且要使扩建后的池塘呈平行四边形形状. 张大伯这一设想是
否能实现?请你帮助他解决
一下,并画出草图.
感悟新知
解:张大伯能实现这一设想.有多种设计方案,现列举两种如下:
方案一:如图①,连结AC.过点D作DH∥AC,且使DH=AC,连结HA,过点B作AC的平行线,延长HA,DC,分别交过点B且平行于AC的直线于点E,F,则四边形EFDH即为扩建后的平行四边形池塘.
感悟新知
方案二:如图②,连结AC,BD.分别过点B,D作AC的平行线,分别过点A,C作BD的平行线,这两组平行线的交点分别为点E,F,G,H,则四边形EFGH即为扩建后的平行四边形池塘.(设计方案不唯一)
本节小结
平行四边形的性质
平行四边形
定义
表示方法
性质
平行线间的距离
请完成教材课后习题
作业提升
