6.2.2.2排列数的应用 课件(共17张PPT)
文档属性
| 名称 | 6.2.2.2排列数的应用 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 529.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
数学
第六章 计数原理
§6.2.2排列数的应用
=n(n-1) (n-2) ┈(n-m+1)
排列数公式:
连乘形式
全排列数公式:
=
=n!
阶乘形式
连乘形式
阶乘形式
规定:
说明:排列数公式的连乘形式常用来计算,
阶乘形式常用来化简或证明。
解题时要灵活地运用如下变式:
复习回顾
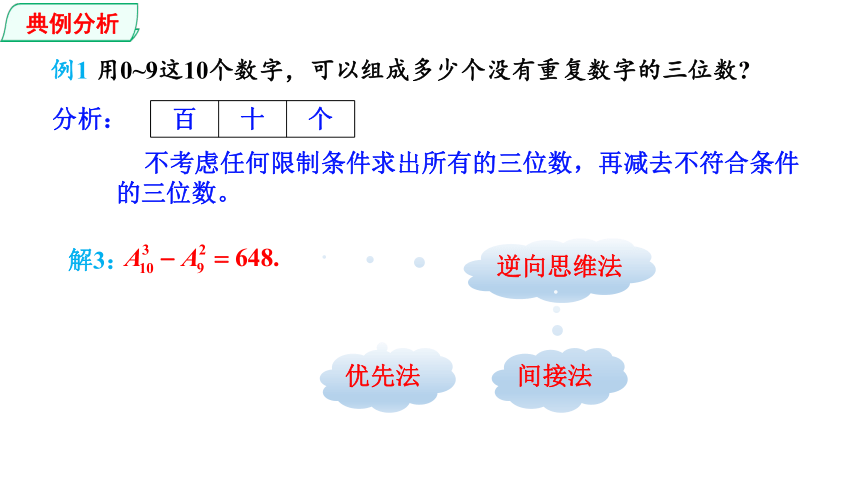
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
解1:
由分步计数原理可得,所求的三位数的个数为
分两步完成:
(1) 从1到9这九个数中任选一个占据百位,有 种方法.
(2) 从余下的9个数(包括数字0)中任选2个占据十位, 个位,有 种方法.
分析:
百位不能为0,可以优先考虑百位数
特殊位置优先法
典例分析
0不能在百位,可以优先考虑0的位置
符合条件的三位数可以分三类:
由分类计数原理可得,所求的三位数的个数为
解2:
(1) 每一位数字都不是0的三位数有 个;
(2) 个位数字是0的三位数有 个;
(3) 十位数字是0的三位数有 个.
特殊元素优先法
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
分析:
典例分析
不考虑任何限制条件求出所有的三位数,再减去不符合条件的三位数。
解3:
逆向思维法
间接法
优先法
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
分析:
典例分析
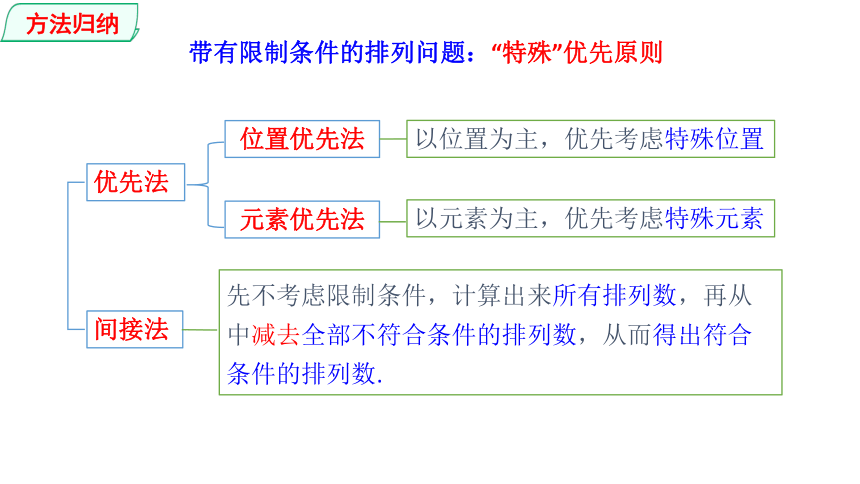
带有限制条件的排列问题:“特殊”优先原则
优先法
间接法
位置优先法
元素优先法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件,计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数.
方法归纳
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
(2) 全体站成一排,甲、乙均不在两端;
(3) 全体站成一排,甲不在最左端,乙不在最右端;
(4) 全体站成一排,男生站在一起、女生站在一起;
(5) 全体站成一排,男生彼此不相邻;
(6) 全体站成一排,男生各不相邻、女生各不相邻;
(7) 全体站成一排,甲、乙中间有2个人;
(8) 排成前后两排,前排3人,后排4人.
排队问题
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【方法总结】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
无条件排列
直接用排列数公式
解:无条件的排列问题,排法有
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(2) 全体站成一排,甲、乙均不在两端;
分析:
特殊位置或特殊元素法
解:先安排甲、乙,有种方法,再安排余下的5人,有种方法,故排法有种).
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(3) 全体站成一排,甲不在最左端,乙不在最右端;
分析:
特殊位置或特殊元素法
解:解法一:直接法
第一类:甲排在最右端,先排乙有6种排法,再排剩余的人有种排法,故排法有6×种排法;
第二类:甲不排在最右端则甲有5种排法,接着排乙有5种排法,最后,排剩余的人有种排法,故排法有5×5×种排法;
由分类加法计数原理,排法有6×+5×5×=3720(种)
解法二:间接法
排法由题知甲在最左端或乙在最右端的排法均有种,甲在最左端且乙在最右端的排法有种,故排法有(种).
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(4) 全体站成一排,男生站在一起、女生站在一起;
解:(1)把男生看成一个整体,男生全排列的排法有种,
(2)再把女生看成一个整体,女生全排列的排法有种,
(3)再把这两个整体全排列,共有(种)排法.
分析:
整体性问题
捆绑法
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(5) 全体站成一排,男生彼此不相邻;
分析:
不相邻问题
插空法
解:先排女生,有种排法,排好后有5个空位,让男生插入5个空位中,有种排法,故共有(种)排法.
可以先排男生吗?
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(6) 全体站成一排,男生各不相邻、女生各不相邻;
解:先排男生,有种排法,让女生插空,有种排法,故共有(种)排法.
分析:
不相邻问题
插空法
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(7) 全体站成一排,甲、乙中间有2个人;
分析:
解:(捆绑法)任选2人与甲、乙组成一个整体,与余下3个元素全排列,故共有(种)排法.
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(8) 排成前后两排,前排3人,后排4人.
分析:
分排问题
直排法
解: 排法有(种).
排队问题
【返回题目】
典例分析
求解排列应用问题的方法:
捆绑法:对于“相邻” 问题,即把相邻元素看作一个整体与其
他元素一起排列,同时注意捆绑元素的内部排列
插空法:对“不相邻” 问题,先考虑不受限制的元素的排列,
再将不相邻的元素插在前面元素排列的空位中
优先法:优先安排特殊元素或特殊位置
直接法:把符合条件的排列数直接列式计算
间接法:先不考虑限制条件,计算出来所有排列数,再从中减去全
部不符合条件的排列数.
课堂小结
[素养小结]
排队问题的解题策略
(1)合理归类: 要将题目大致归类,常见的类型有特殊元素、特殊位置、相邻问题、不相邻问题等,再针对每一类采用相应的方法解题.
(2)恰当结合: 排列问题的解决离不开两个计数原理的应用,解题过程中要恰当结合两个计数原理.
(3)正难则反: 这是一个基本的数学思想,巧妙应用排除法可起到事半功倍的效果.
数学
第六章 计数原理
§6.2.2排列数的应用
=n(n-1) (n-2) ┈(n-m+1)
排列数公式:
连乘形式
全排列数公式:
=
=n!
阶乘形式
连乘形式
阶乘形式
规定:
说明:排列数公式的连乘形式常用来计算,
阶乘形式常用来化简或证明。
解题时要灵活地运用如下变式:
复习回顾
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
解1:
由分步计数原理可得,所求的三位数的个数为
分两步完成:
(1) 从1到9这九个数中任选一个占据百位,有 种方法.
(2) 从余下的9个数(包括数字0)中任选2个占据十位, 个位,有 种方法.
分析:
百位不能为0,可以优先考虑百位数
特殊位置优先法
典例分析
0不能在百位,可以优先考虑0的位置
符合条件的三位数可以分三类:
由分类计数原理可得,所求的三位数的个数为
解2:
(1) 每一位数字都不是0的三位数有 个;
(2) 个位数字是0的三位数有 个;
(3) 十位数字是0的三位数有 个.
特殊元素优先法
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
分析:
典例分析
不考虑任何限制条件求出所有的三位数,再减去不符合条件的三位数。
解3:
逆向思维法
间接法
优先法
例1 用0~9这10个数字,可以组成多少个没有重复数字的三位数
百 十 个
分析:
典例分析
带有限制条件的排列问题:“特殊”优先原则
优先法
间接法
位置优先法
元素优先法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件,计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数.
方法归纳
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
(2) 全体站成一排,甲、乙均不在两端;
(3) 全体站成一排,甲不在最左端,乙不在最右端;
(4) 全体站成一排,男生站在一起、女生站在一起;
(5) 全体站成一排,男生彼此不相邻;
(6) 全体站成一排,男生各不相邻、女生各不相邻;
(7) 全体站成一排,甲、乙中间有2个人;
(8) 排成前后两排,前排3人,后排4人.
排队问题
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【答案】
【方法总结】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(1) 选5人排成一排;
无条件排列
直接用排列数公式
解:无条件的排列问题,排法有
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(2) 全体站成一排,甲、乙均不在两端;
分析:
特殊位置或特殊元素法
解:先安排甲、乙,有种方法,再安排余下的5人,有种方法,故排法有种).
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(3) 全体站成一排,甲不在最左端,乙不在最右端;
分析:
特殊位置或特殊元素法
解:解法一:直接法
第一类:甲排在最右端,先排乙有6种排法,再排剩余的人有种排法,故排法有6×种排法;
第二类:甲不排在最右端则甲有5种排法,接着排乙有5种排法,最后,排剩余的人有种排法,故排法有5×5×种排法;
由分类加法计数原理,排法有6×+5×5×=3720(种)
解法二:间接法
排法由题知甲在最左端或乙在最右端的排法均有种,甲在最左端且乙在最右端的排法有种,故排法有(种).
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(4) 全体站成一排,男生站在一起、女生站在一起;
解:(1)把男生看成一个整体,男生全排列的排法有种,
(2)再把女生看成一个整体,女生全排列的排法有种,
(3)再把这两个整体全排列,共有(种)排法.
分析:
整体性问题
捆绑法
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(5) 全体站成一排,男生彼此不相邻;
分析:
不相邻问题
插空法
解:先排女生,有种排法,排好后有5个空位,让男生插入5个空位中,有种排法,故共有(种)排法.
可以先排男生吗?
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(6) 全体站成一排,男生各不相邻、女生各不相邻;
解:先排男生,有种排法,让女生插空,有种排法,故共有(种)排法.
分析:
不相邻问题
插空法
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(7) 全体站成一排,甲、乙中间有2个人;
分析:
解:(捆绑法)任选2人与甲、乙组成一个整体,与余下3个元素全排列,故共有(种)排法.
排队问题
【返回题目】
典例分析
例2 3名男生和4名女生按照不同的要求排队,求不同的排队方法数.
(8) 排成前后两排,前排3人,后排4人.
分析:
分排问题
直排法
解: 排法有
排队问题
【返回题目】
典例分析
求解排列应用问题的方法:
捆绑法:对于“相邻” 问题,即把相邻元素看作一个整体与其
他元素一起排列,同时注意捆绑元素的内部排列
插空法:对“不相邻” 问题,先考虑不受限制的元素的排列,
再将不相邻的元素插在前面元素排列的空位中
优先法:优先安排特殊元素或特殊位置
直接法:把符合条件的排列数直接列式计算
间接法:先不考虑限制条件,计算出来所有排列数,再从中减去全
部不符合条件的排列数.
课堂小结
[素养小结]
排队问题的解题策略
(1)合理归类: 要将题目大致归类,常见的类型有特殊元素、特殊位置、相邻问题、不相邻问题等,再针对每一类采用相应的方法解题.
(2)恰当结合: 排列问题的解决离不开两个计数原理的应用,解题过程中要恰当结合两个计数原理.
(3)正难则反: 这是一个基本的数学思想,巧妙应用排除法可起到事半功倍的效果.
