3.3几个三角恒等式目标检测(一)[下学期]
文档属性
| 名称 | 3.3几个三角恒等式目标检测(一)[下学期] |
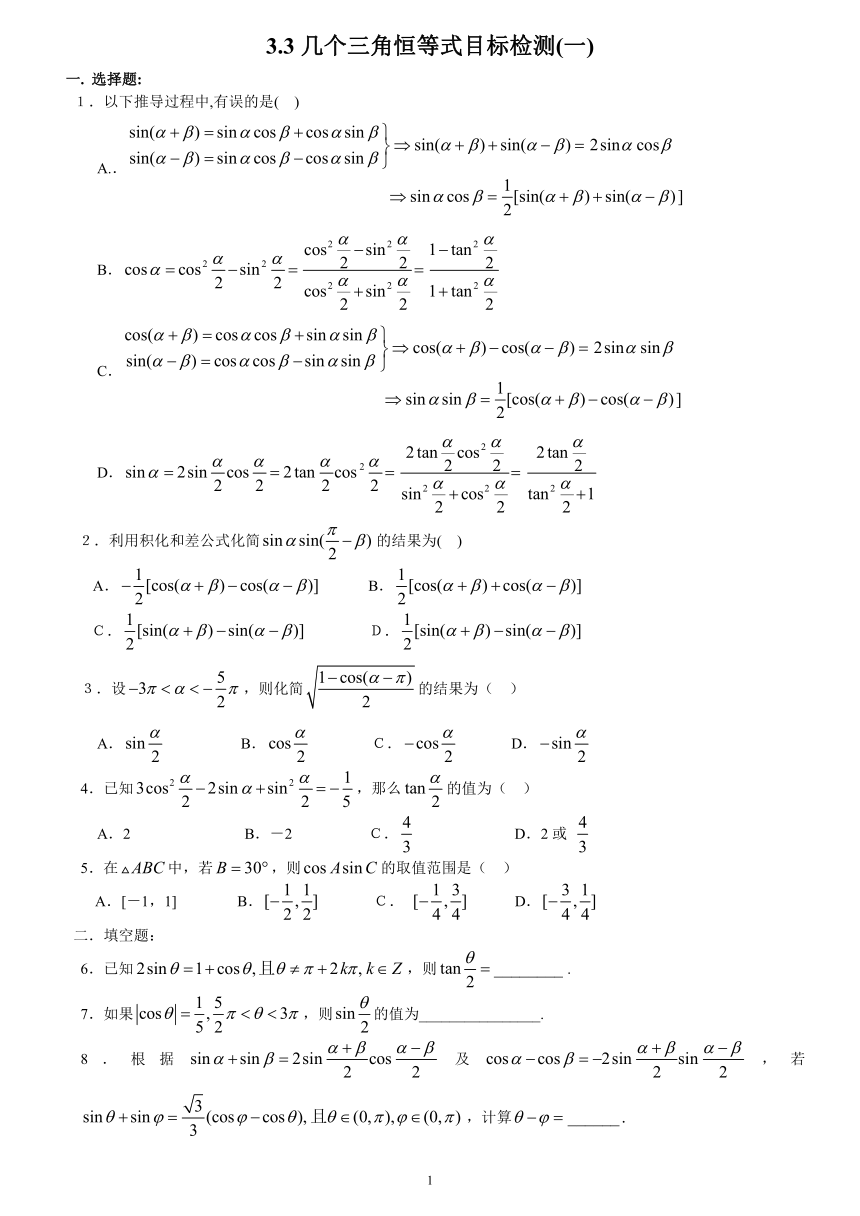
|
|
| 格式 | rar | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-01 00:00:00 | ||
图片预览
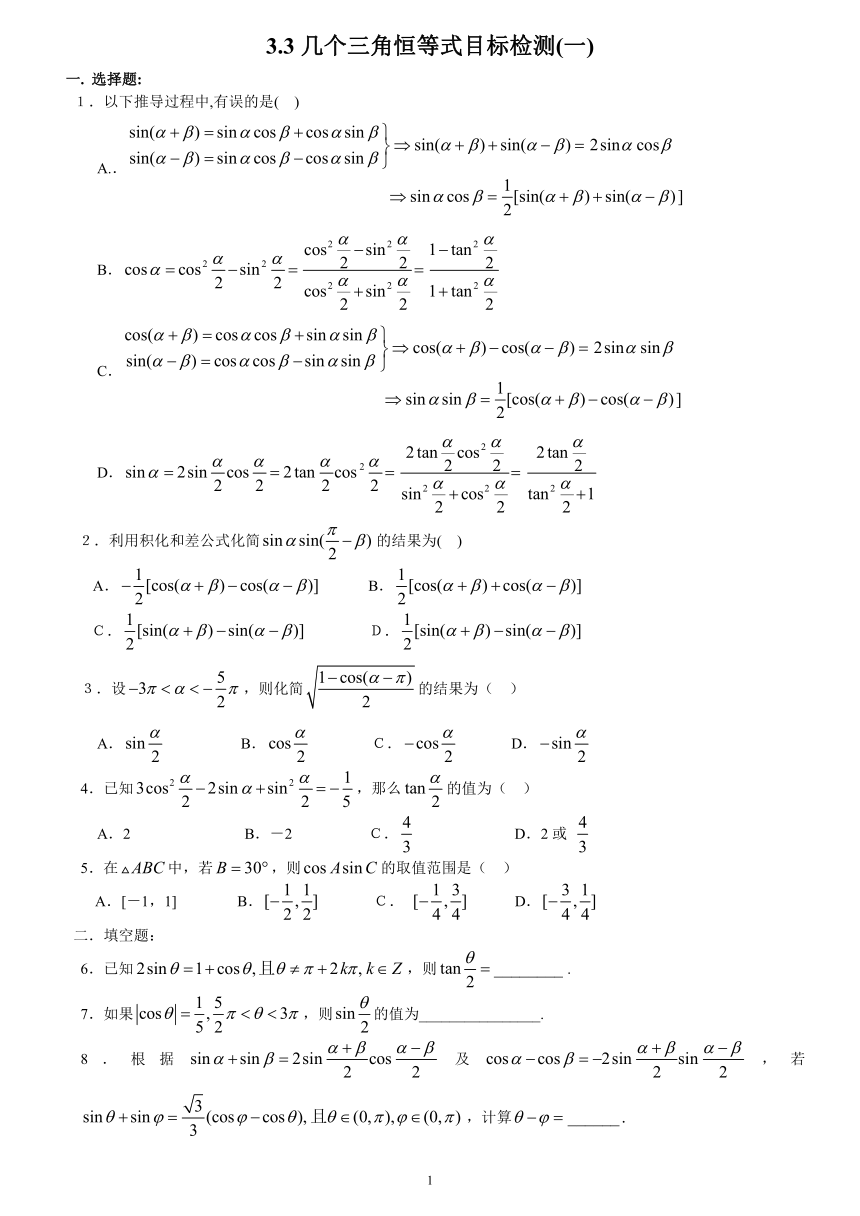


文档简介
3.3几个三角恒等式目标检测(一)
选择题:
1.以下推导过程中,有误的是( )
A..
B.
C.
D.
2.利用积化和差公式化简的结果为( )
A. B.
C. D.
3.设,则化简的结果为( )
A. B. C. D.
4.已知,那么的值为( )
A.2 B.-2 C. D.2或
5.在中,若,则的取值范围是( )
A.[-1,1] B. C. D.
二.填空题:
6.已知,则.
7.如果,则的值为________________.
8.根据及,若,计算
9.函数的最大值为_________.
三.解答题:
10.根据你所掌握的知识,试求出的值.
11.已知,试求出的值.
12.(1)试用万能公式证明:.
(2)已知,当为第二象限角时,利用(1)的结论求的值.
几个三角恒等式目标检测(一)参考答案
一.1.C 考查学生推导几个恒等式的能力,参见教参
2.D 参见课本P114练习题第1题
3.C 考查半角公式的简单应用,参见课本P115练习题第3题
4.D 参见课本P113链接
5.C 考查积化和差公式简单的应用
二.6. 考查万能公式简单的应用(本题也可用倍角公式求解)
7. 参见课本P115练习题第3题
8. 参见课本P115练习题第2题
9. 参见课本P117第12题,考查积化和差公式简单的应用
(本题也可用诱导公式变形求解)
三.
10.法一:由得 解得.
法二:构造图形
如图,令AC=BC=1,ACB=,则AB=
延长CB至D,使得BD=AB,易得ADB=
在ACB中,.
本题考查学生对角是角的一半的认识程度,可考虑用万能公式,也可以从几何图形构造出的角进行求解。
11.法一:由,得
由,得
法二:由, 得,
从而,
本题参见课本P115练习题第3题
12.(1)证明:由及得
故.
(2)解:由为第二象限角 得
由(1)得 .
本题设计参见课本P113链接。
3.3 几个三角恒等式目标检测(二)
一.选择题:
1.若,则的值为( )
A. B.1 C. D.
2.若,则=( )
A. B. C. D.
3.在中,若,则是( )
A.等边三角形 B.等腰三角形 C.不等边三角形 D.直角三角形
4.已知等腰三角形顶角的余弦值为,则底角的余弦值为( )
A. B. C. D.
5.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
二.填空题:
6.的值为_______________.
7.若,则_________;=___________.
8.化简的结果为____________.
三.解答题:
9.已知,求①的值;②.
10.已知为第四象限角,求的值.
11.设.
(1)求证: ;
(2)当时,利用以上结果求的值.
几个三角恒等式目标检测(二)参考答案
一.1.B 参见课本P114思考(2),考查万能代换
2.B 参见课本P117练习题第1题,考查积化和差公式简单得应用
3.B 参见课本P115练习题第3题,考查半角公式的简单应用
4.A 参见课本P117
5.D 考查积化和差公式简单的应用
二.6.0 考查积化和差公式公式简单的应用,参见课本P115练习题第3题
7.3, 考查万能代换及半角公式简单的应用
8. 考查万能公式简单的应用
三.9. 解:由,得
,,
本题考查万能代换,参见课本P 113链接
10.解:由为第四象限角,得为第二或第四象限角.
(1)当为第二象限角时,
(2)当为第四象限角时,,,.
本题解法较多,主要考查半角公式简单的应用,参见课本P115练习题第3题
11.(1)证明:由及得
,
故.
(2)解:由(1)及 得
=
本题设计参见课本P113链接。
选择题:
1.以下推导过程中,有误的是( )
A..
B.
C.
D.
2.利用积化和差公式化简的结果为( )
A. B.
C. D.
3.设,则化简的结果为( )
A. B. C. D.
4.已知,那么的值为( )
A.2 B.-2 C. D.2或
5.在中,若,则的取值范围是( )
A.[-1,1] B. C. D.
二.填空题:
6.已知,则.
7.如果,则的值为________________.
8.根据及,若,计算
9.函数的最大值为_________.
三.解答题:
10.根据你所掌握的知识,试求出的值.
11.已知,试求出的值.
12.(1)试用万能公式证明:.
(2)已知,当为第二象限角时,利用(1)的结论求的值.
几个三角恒等式目标检测(一)参考答案
一.1.C 考查学生推导几个恒等式的能力,参见教参
2.D 参见课本P114练习题第1题
3.C 考查半角公式的简单应用,参见课本P115练习题第3题
4.D 参见课本P113链接
5.C 考查积化和差公式简单的应用
二.6. 考查万能公式简单的应用(本题也可用倍角公式求解)
7. 参见课本P115练习题第3题
8. 参见课本P115练习题第2题
9. 参见课本P117第12题,考查积化和差公式简单的应用
(本题也可用诱导公式变形求解)
三.
10.法一:由得 解得.
法二:构造图形
如图,令AC=BC=1,ACB=,则AB=
延长CB至D,使得BD=AB,易得ADB=
在ACB中,.
本题考查学生对角是角的一半的认识程度,可考虑用万能公式,也可以从几何图形构造出的角进行求解。
11.法一:由,得
由,得
法二:由, 得,
从而,
本题参见课本P115练习题第3题
12.(1)证明:由及得
故.
(2)解:由为第二象限角 得
由(1)得 .
本题设计参见课本P113链接。
3.3 几个三角恒等式目标检测(二)
一.选择题:
1.若,则的值为( )
A. B.1 C. D.
2.若,则=( )
A. B. C. D.
3.在中,若,则是( )
A.等边三角形 B.等腰三角形 C.不等边三角形 D.直角三角形
4.已知等腰三角形顶角的余弦值为,则底角的余弦值为( )
A. B. C. D.
5.函数是( )
A.周期为的奇函数 B.周期为的奇函数
C.周期为的偶函数 D.周期为的偶函数
二.填空题:
6.的值为_______________.
7.若,则_________;=___________.
8.化简的结果为____________.
三.解答题:
9.已知,求①的值;②.
10.已知为第四象限角,求的值.
11.设.
(1)求证: ;
(2)当时,利用以上结果求的值.
几个三角恒等式目标检测(二)参考答案
一.1.B 参见课本P114思考(2),考查万能代换
2.B 参见课本P117练习题第1题,考查积化和差公式简单得应用
3.B 参见课本P115练习题第3题,考查半角公式的简单应用
4.A 参见课本P117
5.D 考查积化和差公式简单的应用
二.6.0 考查积化和差公式公式简单的应用,参见课本P115练习题第3题
7.3, 考查万能代换及半角公式简单的应用
8. 考查万能公式简单的应用
三.9. 解:由,得
,,
本题考查万能代换,参见课本P 113链接
10.解:由为第四象限角,得为第二或第四象限角.
(1)当为第二象限角时,
(2)当为第四象限角时,,,.
本题解法较多,主要考查半角公式简单的应用,参见课本P115练习题第3题
11.(1)证明:由及得
,
故.
(2)解:由(1)及 得
=
本题设计参见课本P113链接。
