人教版数学七年级下册5.1.2 垂线 同步练习(含答案)
文档属性
| 名称 | 人教版数学七年级下册5.1.2 垂线 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 377.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 00:00:00 | ||
图片预览

文档简介
5.1.2 垂线 同步练习
一、单选题
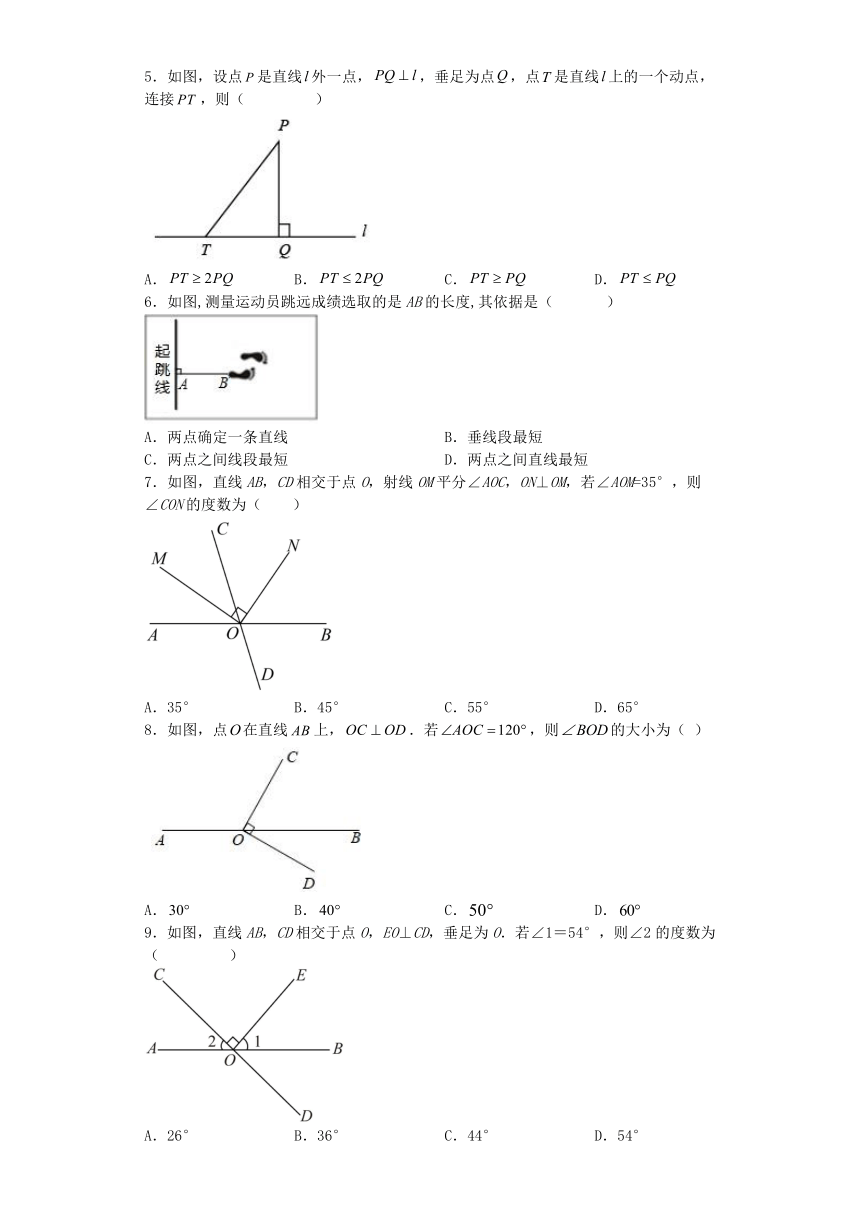
1.如图,P为直线l外一点,A,B,C在l上,且PB⊥l,下列说法中,正确的个数是( )
①PA,PB,PC三条线段中,PB最短;②线段PB叫做点P到直线l的距离;③线段AB的长是点A到PB的距离;④线段AC的长是点A到PC的距离.
A.1个 B.2个 C.3个 D.4个
2.下列图形中,线段的长表示点A到直线的距离的是( )
A. B.
C. D.
3.如图,,,表示点到直线距离的是线段( )的长度
A. B. C. D.
4.点P为直线外一点,点A、B、C为直线上三点,,,,则P到直线的距离为( )
A. B. C.小于 D.不大于
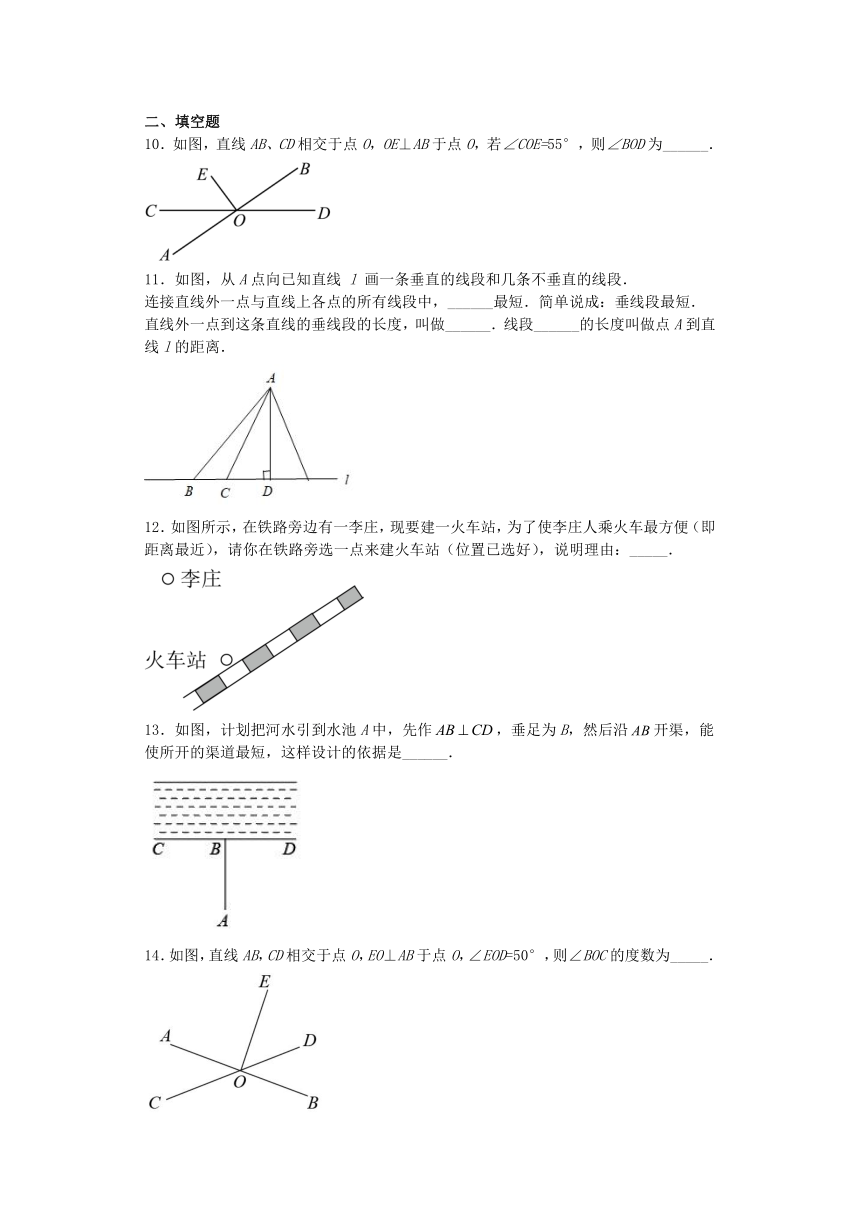
5.如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连接,则( )
A. B. C. D.
6.如图,测量运动员跳远成绩选取的是AB的长度,其依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.两点之间直线最短
7.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
8.如图,点在直线上,.若,则的大小为( )
A. B. C. D.
9.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
二、填空题
10.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
11.如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
连接直线外一点与直线上各点的所有线段中,______最短.简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做______.线段______的长度叫做点A到直线l的距离.
12.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:_____.
13.如图,计划把河水引到水池A中,先作,垂足为B,然后沿开渠,能使所开的渠道最短,这样设计的依据是______.
14.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为_____.
三、解答题
15.如图所示,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线段PE.
(2)过点P画CD的垂线,与AB相交于F点.
(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?
16.如图,为解决A、B、C、D四个村庄的用水问题.政府准备投资修建一个蓄水池.
(1)若使蓄水池与四个村庄的距离的和最小,请画出蓄水池P的位置;
(2)为把河道l中的水引入蓄水池P中,需要再修建一条引水渠.若使引水渠的长度最小,请画出引水渠PQ的修建线路.
17.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠EOF=55°,OD⊥OF,求∠AOC的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠DOE的度数.
参考答案:
1.B
2.B
3.B
4.D
5.C
6.B
7.C
8.A
9.B
10.35°
11. 垂线段 点到直线的距离 AD
12.垂线段最短
【详解】解:从直线外一点到这条直线上各点所连的线段中,垂线段最短,
13.连接直线外一点与直线上所有点的连线中,垂线段最短
【详解】
解:∵连接直线外一点与直线上所有点的连线中,垂线段最短,
∴沿开渠,能使所开的渠道最短,
故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.
14.140°##140度
【详解】解:∵直线AB,CD相交于点O,EO⊥AB于点O,
∴∠EOB=90°,
∵∠EOD=50°,
∴∠BOD=40°,
则∠BOC的度数为:180°-40°=140°.
故答案为140°.
15.
【详解】(1)(2)如图所示.
(3)在直角△FPO中,PO<FO,
在直角△PEO中,PE<PO,
∴PE<PO<FO,其依据是“垂线段最短”.
16.
【详解】解答:解:(1)如图所示:由两点之间,线段最短,连接AC、BD交点即为P点,
(2)如图所示:由垂线段最短,过P作PQ⊥河道l,垂足即为Q点.
17.
【详解】(1)解:∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠EOF=55°,OD⊥OF,
∴∠DOE=35°,
∴∠BOE=35°,
∴∠AOC=70°;
(2)∵OF平分∠COE,
∴∠COF=∠EOF,
∵∠BOF=15°,
∴设∠DOE=∠BOE=x,
则∠COF=x+15°,
∴x+15°+x+15°+x=180°,
解得:x=50°,
故∠DOE的度数为:50°.
一、单选题
1.如图,P为直线l外一点,A,B,C在l上,且PB⊥l,下列说法中,正确的个数是( )
①PA,PB,PC三条线段中,PB最短;②线段PB叫做点P到直线l的距离;③线段AB的长是点A到PB的距离;④线段AC的长是点A到PC的距离.
A.1个 B.2个 C.3个 D.4个
2.下列图形中,线段的长表示点A到直线的距离的是( )
A. B.
C. D.
3.如图,,,表示点到直线距离的是线段( )的长度
A. B. C. D.
4.点P为直线外一点,点A、B、C为直线上三点,,,,则P到直线的距离为( )
A. B. C.小于 D.不大于
5.如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连接,则( )
A. B. C. D.
6.如图,测量运动员跳远成绩选取的是AB的长度,其依据是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.两点之间直线最短
7.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.35° B.45° C.55° D.65°
8.如图,点在直线上,.若,则的大小为( )
A. B. C. D.
9.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
二、填空题
10.如图,直线AB、CD相交于点O,OE⊥AB于点O,若∠COE=55°,则∠BOD为______.
11.如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
连接直线外一点与直线上各点的所有线段中,______最短.简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做______.线段______的长度叫做点A到直线l的距离.
12.如图所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:_____.
13.如图,计划把河水引到水池A中,先作,垂足为B,然后沿开渠,能使所开的渠道最短,这样设计的依据是______.
14.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为_____.
三、解答题
15.如图所示,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线段PE.
(2)过点P画CD的垂线,与AB相交于F点.
(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?
16.如图,为解决A、B、C、D四个村庄的用水问题.政府准备投资修建一个蓄水池.
(1)若使蓄水池与四个村庄的距离的和最小,请画出蓄水池P的位置;
(2)为把河道l中的水引入蓄水池P中,需要再修建一条引水渠.若使引水渠的长度最小,请画出引水渠PQ的修建线路.
17.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠EOF=55°,OD⊥OF,求∠AOC的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠DOE的度数.
参考答案:
1.B
2.B
3.B
4.D
5.C
6.B
7.C
8.A
9.B
10.35°
11. 垂线段 点到直线的距离 AD
12.垂线段最短
【详解】解:从直线外一点到这条直线上各点所连的线段中,垂线段最短,
13.连接直线外一点与直线上所有点的连线中,垂线段最短
【详解】
解:∵连接直线外一点与直线上所有点的连线中,垂线段最短,
∴沿开渠,能使所开的渠道最短,
故答案为:连接直线外一点与直线上所有点的连线中,垂线段最短.
14.140°##140度
【详解】解:∵直线AB,CD相交于点O,EO⊥AB于点O,
∴∠EOB=90°,
∵∠EOD=50°,
∴∠BOD=40°,
则∠BOC的度数为:180°-40°=140°.
故答案为140°.
15.
【详解】(1)(2)如图所示.
(3)在直角△FPO中,PO<FO,
在直角△PEO中,PE<PO,
∴PE<PO<FO,其依据是“垂线段最短”.
16.
【详解】解答:解:(1)如图所示:由两点之间,线段最短,连接AC、BD交点即为P点,
(2)如图所示:由垂线段最短,过P作PQ⊥河道l,垂足即为Q点.
17.
【详解】(1)解:∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠EOF=55°,OD⊥OF,
∴∠DOE=35°,
∴∠BOE=35°,
∴∠AOC=70°;
(2)∵OF平分∠COE,
∴∠COF=∠EOF,
∵∠BOF=15°,
∴设∠DOE=∠BOE=x,
则∠COF=x+15°,
∴x+15°+x+15°+x=180°,
解得:x=50°,
故∠DOE的度数为:50°.
