吉林省长春市第52中学2022-2023学年第二学期九年级数学第一次月考试题(PDF版,无答案)
文档属性
| 名称 | 吉林省长春市第52中学2022-2023学年第二学期九年级数学第一次月考试题(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 485.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 15:22:49 | ||
图片预览


文档简介
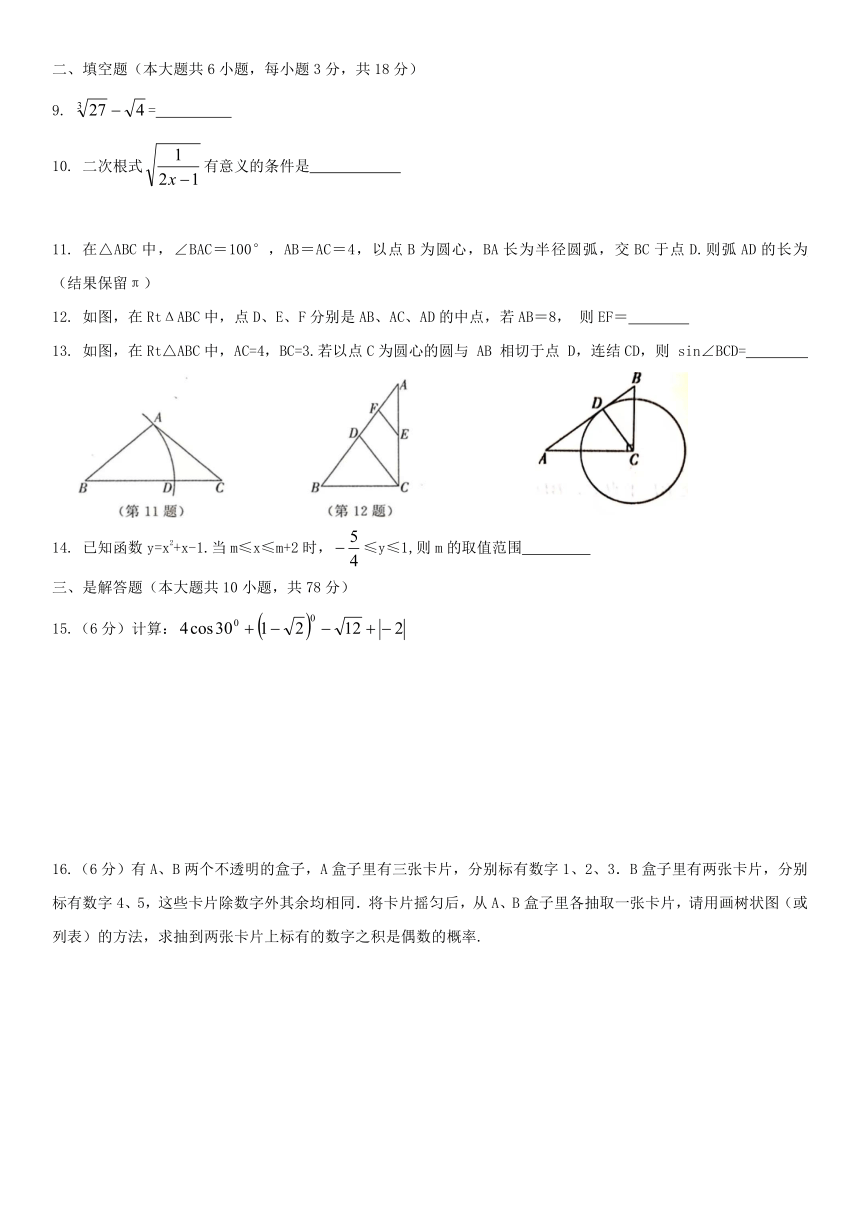
九年级下第一次月考数学试题
一、选择题(本大题共 8小题,每小题 3 分,共 24 分)
1. 下列各式属于最简二次根式的是( )
A. 0.5 1B. 5 C. D. 20
5
2. 方程 x 1 2 9 0的解是( )
A. x1 4, x2 2 B. x1 4, x2 2 C. x1 4, x2 4 D. x1 2, x2 2
a 3 a b
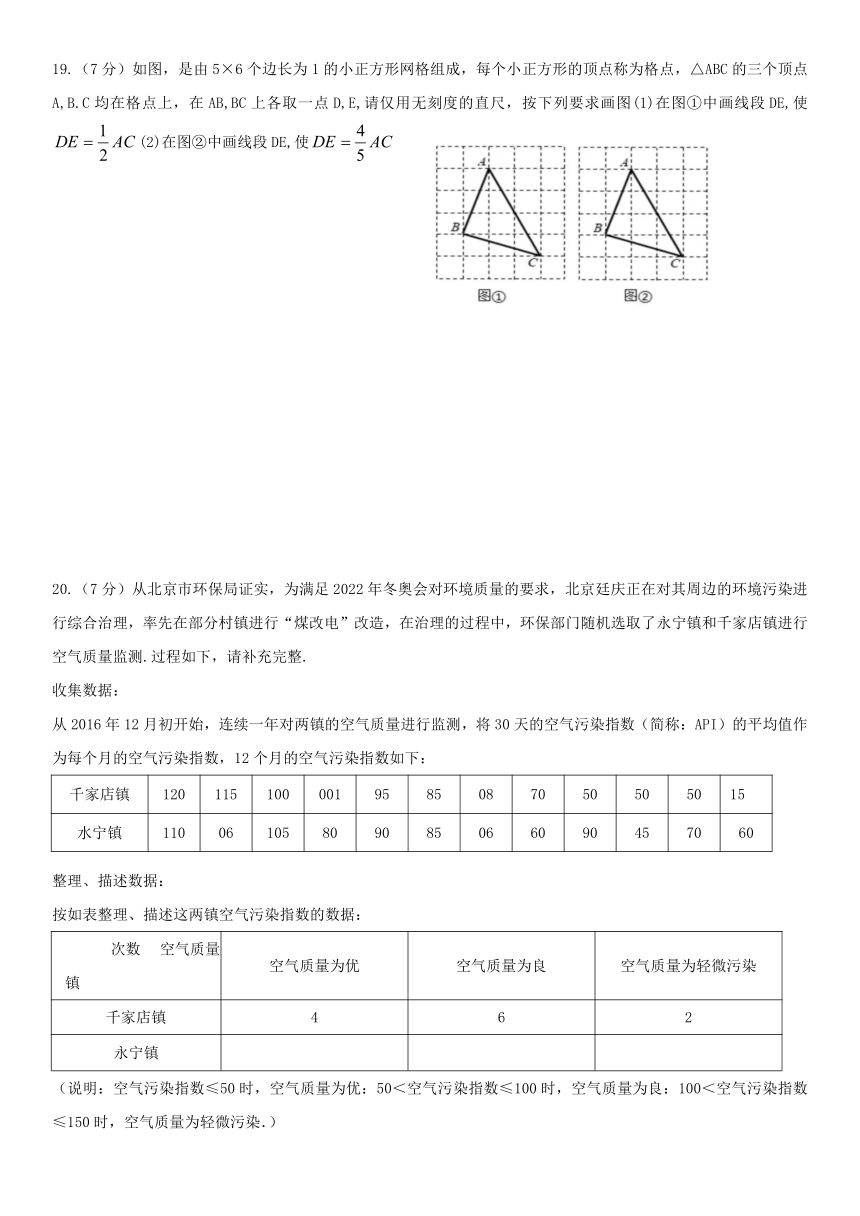
3. 若 ,则 的值为( )
b 2 b
2 5 1
A. B. C.5 D.
5 2 5
4. 下列成语所描述的事件属于不可能事件的是( )
A. 水落石出 B.水滴石穿 C.水中捞月 D.水涨船高
5. 小明沿着坡比为 1: 3的上坡向上走了 100 米,则他升高了( )米
A. 50 3 B.50 C.50 2 D.100
6.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板
来测量距离,在如图所示的测量距离 AB 的示意图中,记照板“内芯”的高度为 EF.观测者的眼睛(图中用点 C 表示)
与 BF 在同一水平线上,则下列结论正确的是( )
CE CF CF EF CE EF CE EF
A. B. C. D.
CA BF BF AB CA AB AE AB
7.如图, o 的直径 AB=2,弦 AC=1,点 D 在 o 上,则∠D的度数是( )
0 0 0 0
A.30 B.45 C.60 D.75
8.某广场有一个小型喷泉,水流从垂直于地面的水管 OA 喷出,OA 长为 1.5m,水流在各个方向上沿形状相同的抛物
线路径落到地面上,某方向上抛物线路径的形状如图所示,落点 B 到 O 的距离为 3m.建立平面直角坐标系,水流
喷出的高度 y(m)与水平距离 x(m)之间近似满足函数关系 y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
3 13
A.1 米 B. 米 C.2 米 D. 米
2 8
二、填空题(本大题共 6小题,每小题 3 分,共 18 分)
9. 3 27 4 =
1
10. 二次根式 有意义的条件是
2x 1
11. 在△ABC 中,∠BAC=100°,AB=AC=4,以点 B 为圆心,BA 长为半径圆弧,交 BC 于点 D.则弧 AD 的长为
(结果保留π)
12. 如图,在 RtΔABC 中,点 D、E、F分别是 AB、AC、AD 的中点,若 AB=8, 则 EF=
13. 如图,在 Rt△ABC 中,AC=4,BC=3.若以点 C 为圆心的圆与 AB 相切于点 D,连结 CD,则 sin∠BCD=
2 5
14. 已知函数 y=x +x-1.当 m≤x≤m+2 时, ≤y≤1,则 m 的取值范围
4
三、是解答题(本大题共 10 小题,共 78 分)
0 0
15.(6 分)计算: 4cos30 1 2 12 2
16.(6 分)有 A、B 两个不透明的盒子,A盒子里有三张卡片,分别标有数字 1、2、3.B 盒子里有两张卡片,分别
标有数字 4、5,这些卡片除数字外其余均相同.将卡片摇匀后,从 A、B 盒子里各抽取一张卡片,请用画树状图(或
列表)的方法,求抽到两张卡片上标有的数字之积是偶数的概率.
17. (6 分)某学校图书馆去年年底有图书 5 万册,预计到明年年底会增加到 7.2 万,求这两年的平均增长率.
18. (7 分) 如图,在⊙O中,AB 是⊙O 的直径,F 是弦 AD 的中点,连结 OF 并延长 OF 交⊙O 于点 E,连结 BE 交 AD
于点 G,延长 AD 至点 C,使得 GC=BC,连结 BC
(1)求证:BC 是⊙O 的切线.
3
(2)⊙O 的半径为 10,sinA= ,则 EG= .
5
19.(7 分)如图,是由 5×6 个边长为 1 的小正方形网格组成,每个小正方形的顶点称为格点,△ABC 的三个顶点
A,B.C 均在格点上,在 AB,BC 上各取一点 D,E,请仅用无刻度的直尺,按下列要求画图(1)在图①中画线段 DE,使
DE 1 4 AC (2)在图②中画线段 DE,使 DE AC
2 5
20.(7 分)从北京市环保局证实,为满足 2022 年冬奥会对环境质量的要求,北京廷庆正在对其周边的环境污染进
行综合治理,率先在部分村镇进行“煤改电”改造,在治理的过程中,环保部门随机选取了永宁镇和千家店镇进行
空气质量监测.过程如下,请补充完整.
收集数据:
从 2016 年 12 月初开始,连续一年对两镇的空气质量进行监测,将 30 天的空气污染指数(简称:API)的平均值作
为每个月的空气污染指数,12 个月的空气污染指数如下:
千家店镇 120 115 100 001 95 85 08 70 50 50 50 15
水宁镇 110 06 105 80 90 85 06 60 90 45 70 60
整理、描述数据:
按如表整理、描述这两镇空气污染指数的数据:
次数 空气质量
空气质量为优 空气质量为良 空气质量为轻微污染
镇
千家店镇 4 6 2
永宁镇
(说明:空气污染指数≤50 时,空气质量为优:50<空气污染指数≤100 时,空气质量为良:100<空气污染指数
≤150 时,空气质量为轻微污染.)
分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇 平均数 中位数 众数
千家店镇 80 50
水宁镇 81.3 87.5
请将以上两个表格补充完整:
得出结论:可以推断出 镇这一年中环境状况比较好,理由为(至少从两个不同的角度说明推断的合理性)
21. (8 分)如图,工程队拟沿 AC 方向开山修路,为加快施工进度,需在小山的另一边点 E处同时施工,要使 A,C,E
三点在一条直线上,工程队从 AC 上的一点 B 取∠ABD=1400,BD=560 米,∠D=500,那么点 E 与点 D 间的距离是多少米?
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
22.(9 分)【问题原型】小慧同学遇到这样一道,如图①,在△ABC 中,点 D 为 AC 的中点,以点 D 为圆心,AC 为直
径作圆,∠ACB 的平分线交⊙D 于点 P,点 P在△ABC 内部,连结 BP,求证:△BPC 的面积等于△ABC 面积的一半
【问题解决】小慧的做法是连结 AP 延长、交边 BC 于点 Q,利用△ACQ 形状的特殊性来解决问题,请你利用小慧的做
法完成【问题提出】中的证明
【问题拓展】如图②,在四边形 ABCD 中,AC 平分∠BAD,AC⊥BC.若 BD=8,AB-AD=3,则△BCD 面积的最大值为
3
23.(10 分)如图,在ΔABC 中,AB=BC=5,cosB= ,动点 P 从点 A出发、以每秒 2 个单位的速度向终点 B 运动;
5
当点 P不与 A、B重合时,过点 P 作 BC 的平行线交 AC 于点 M.动点 Q 从点 B 出发,以每秒 3个单位的速度向终点 A
运动.以 PQ、PM 为邻边作 PQNM.点 P、Q 同时出发,设运动时间为 t秒.(1)用含 t的代数式表示 PM 的长.(2)
设 PQNM 和ΔABC 重合部分的面积为 S,求 S 与 t 的函数关系式.(3)若点 M 关于直线 QN 的对称点为 M',直接写
出直线 CM'和ΔABC 的边垂直时 t的值
24.(12 分)在平面直角坐标系中,点 A,B 在二次函数 y=x2-2mx+3m(m 是常数)的图像上,A,B 两点之间的部分(包括
A,B 两点)图像记为 G.设点 A,B 两点的横坐标分别为 m+1,3m.
3 2
(1)当 m= 时,求二次函数 y=x -2mx+3m 图像的最低点的坐标.
2
(2)当图像 G 的最高点为点 A,且图像 G对应的函数值 y 随 x 的增大而增大时,求 m的取值范围.、
(3)设图像 G 的最高点的纵坐标与最低点的纵坐标的差为 h,当图像 G 的最高点只有点 B 时,求 h 与 m 之间的函数关
系式
(4)设图像G的最高点与最低点分别为M,N,以 M,N为对角线作矩形MPNQ,若矩形MPNQ 的周长为4,求 m的取值范围.
8
一、选择题(本大题共 8小题,每小题 3 分,共 24 分)
1. 下列各式属于最简二次根式的是( )
A. 0.5 1B. 5 C. D. 20
5
2. 方程 x 1 2 9 0的解是( )
A. x1 4, x2 2 B. x1 4, x2 2 C. x1 4, x2 4 D. x1 2, x2 2
a 3 a b
3. 若 ,则 的值为( )
b 2 b
2 5 1
A. B. C.5 D.
5 2 5
4. 下列成语所描述的事件属于不可能事件的是( )
A. 水落石出 B.水滴石穿 C.水中捞月 D.水涨船高
5. 小明沿着坡比为 1: 3的上坡向上走了 100 米,则他升高了( )米
A. 50 3 B.50 C.50 2 D.100
6.中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板
来测量距离,在如图所示的测量距离 AB 的示意图中,记照板“内芯”的高度为 EF.观测者的眼睛(图中用点 C 表示)
与 BF 在同一水平线上,则下列结论正确的是( )
CE CF CF EF CE EF CE EF
A. B. C. D.
CA BF BF AB CA AB AE AB
7.如图, o 的直径 AB=2,弦 AC=1,点 D 在 o 上,则∠D的度数是( )
0 0 0 0
A.30 B.45 C.60 D.75
8.某广场有一个小型喷泉,水流从垂直于地面的水管 OA 喷出,OA 长为 1.5m,水流在各个方向上沿形状相同的抛物
线路径落到地面上,某方向上抛物线路径的形状如图所示,落点 B 到 O 的距离为 3m.建立平面直角坐标系,水流
喷出的高度 y(m)与水平距离 x(m)之间近似满足函数关系 y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
3 13
A.1 米 B. 米 C.2 米 D. 米
2 8
二、填空题(本大题共 6小题,每小题 3 分,共 18 分)
9. 3 27 4 =
1
10. 二次根式 有意义的条件是
2x 1
11. 在△ABC 中,∠BAC=100°,AB=AC=4,以点 B 为圆心,BA 长为半径圆弧,交 BC 于点 D.则弧 AD 的长为
(结果保留π)
12. 如图,在 RtΔABC 中,点 D、E、F分别是 AB、AC、AD 的中点,若 AB=8, 则 EF=
13. 如图,在 Rt△ABC 中,AC=4,BC=3.若以点 C 为圆心的圆与 AB 相切于点 D,连结 CD,则 sin∠BCD=
2 5
14. 已知函数 y=x +x-1.当 m≤x≤m+2 时, ≤y≤1,则 m 的取值范围
4
三、是解答题(本大题共 10 小题,共 78 分)
0 0
15.(6 分)计算: 4cos30 1 2 12 2
16.(6 分)有 A、B 两个不透明的盒子,A盒子里有三张卡片,分别标有数字 1、2、3.B 盒子里有两张卡片,分别
标有数字 4、5,这些卡片除数字外其余均相同.将卡片摇匀后,从 A、B 盒子里各抽取一张卡片,请用画树状图(或
列表)的方法,求抽到两张卡片上标有的数字之积是偶数的概率.
17. (6 分)某学校图书馆去年年底有图书 5 万册,预计到明年年底会增加到 7.2 万,求这两年的平均增长率.
18. (7 分) 如图,在⊙O中,AB 是⊙O 的直径,F 是弦 AD 的中点,连结 OF 并延长 OF 交⊙O 于点 E,连结 BE 交 AD
于点 G,延长 AD 至点 C,使得 GC=BC,连结 BC
(1)求证:BC 是⊙O 的切线.
3
(2)⊙O 的半径为 10,sinA= ,则 EG= .
5
19.(7 分)如图,是由 5×6 个边长为 1 的小正方形网格组成,每个小正方形的顶点称为格点,△ABC 的三个顶点
A,B.C 均在格点上,在 AB,BC 上各取一点 D,E,请仅用无刻度的直尺,按下列要求画图(1)在图①中画线段 DE,使
DE 1 4 AC (2)在图②中画线段 DE,使 DE AC
2 5
20.(7 分)从北京市环保局证实,为满足 2022 年冬奥会对环境质量的要求,北京廷庆正在对其周边的环境污染进
行综合治理,率先在部分村镇进行“煤改电”改造,在治理的过程中,环保部门随机选取了永宁镇和千家店镇进行
空气质量监测.过程如下,请补充完整.
收集数据:
从 2016 年 12 月初开始,连续一年对两镇的空气质量进行监测,将 30 天的空气污染指数(简称:API)的平均值作
为每个月的空气污染指数,12 个月的空气污染指数如下:
千家店镇 120 115 100 001 95 85 08 70 50 50 50 15
水宁镇 110 06 105 80 90 85 06 60 90 45 70 60
整理、描述数据:
按如表整理、描述这两镇空气污染指数的数据:
次数 空气质量
空气质量为优 空气质量为良 空气质量为轻微污染
镇
千家店镇 4 6 2
永宁镇
(说明:空气污染指数≤50 时,空气质量为优:50<空气污染指数≤100 时,空气质量为良:100<空气污染指数
≤150 时,空气质量为轻微污染.)
分析数据:
两镇的空气污染指数的平均数、中位数、众数如表所示:
城镇 平均数 中位数 众数
千家店镇 80 50
水宁镇 81.3 87.5
请将以上两个表格补充完整:
得出结论:可以推断出 镇这一年中环境状况比较好,理由为(至少从两个不同的角度说明推断的合理性)
21. (8 分)如图,工程队拟沿 AC 方向开山修路,为加快施工进度,需在小山的另一边点 E处同时施工,要使 A,C,E
三点在一条直线上,工程队从 AC 上的一点 B 取∠ABD=1400,BD=560 米,∠D=500,那么点 E 与点 D 间的距离是多少米?
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
22.(9 分)【问题原型】小慧同学遇到这样一道,如图①,在△ABC 中,点 D 为 AC 的中点,以点 D 为圆心,AC 为直
径作圆,∠ACB 的平分线交⊙D 于点 P,点 P在△ABC 内部,连结 BP,求证:△BPC 的面积等于△ABC 面积的一半
【问题解决】小慧的做法是连结 AP 延长、交边 BC 于点 Q,利用△ACQ 形状的特殊性来解决问题,请你利用小慧的做
法完成【问题提出】中的证明
【问题拓展】如图②,在四边形 ABCD 中,AC 平分∠BAD,AC⊥BC.若 BD=8,AB-AD=3,则△BCD 面积的最大值为
3
23.(10 分)如图,在ΔABC 中,AB=BC=5,cosB= ,动点 P 从点 A出发、以每秒 2 个单位的速度向终点 B 运动;
5
当点 P不与 A、B重合时,过点 P 作 BC 的平行线交 AC 于点 M.动点 Q 从点 B 出发,以每秒 3个单位的速度向终点 A
运动.以 PQ、PM 为邻边作 PQNM.点 P、Q 同时出发,设运动时间为 t秒.(1)用含 t的代数式表示 PM 的长.(2)
设 PQNM 和ΔABC 重合部分的面积为 S,求 S 与 t 的函数关系式.(3)若点 M 关于直线 QN 的对称点为 M',直接写
出直线 CM'和ΔABC 的边垂直时 t的值
24.(12 分)在平面直角坐标系中,点 A,B 在二次函数 y=x2-2mx+3m(m 是常数)的图像上,A,B 两点之间的部分(包括
A,B 两点)图像记为 G.设点 A,B 两点的横坐标分别为 m+1,3m.
3 2
(1)当 m= 时,求二次函数 y=x -2mx+3m 图像的最低点的坐标.
2
(2)当图像 G 的最高点为点 A,且图像 G对应的函数值 y 随 x 的增大而增大时,求 m的取值范围.、
(3)设图像 G 的最高点的纵坐标与最低点的纵坐标的差为 h,当图像 G 的最高点只有点 B 时,求 h 与 m 之间的函数关
系式
(4)设图像G的最高点与最低点分别为M,N,以 M,N为对角线作矩形MPNQ,若矩形MPNQ 的周长为4,求 m的取值范围.
8
同课章节目录
