多边形单元测试[下学期]
图片预览

文档简介
华师大版数学 第九章《多边形》单元测试
(时间:45分钟,满分:100分)
班级 姓名 学号 成绩
一.填空题(每空3分,共33分)
1.在中,若,,则 .
2.两根木棒的长分别是和,要选择第三根木棒,将它们钉成三角形。
已知第三根木棒长为奇数,则第三根木棒的长度应该等于 .
3.一个多边形内角和为,则这个多边形是 边形;
五边形中一共有 条对角线.
4. 三角形三个内角之比为3:2:5,则最小角等于 (度),
它是 三角形.
5.如图1,,,,那么 , .
6.如图2,在中,,于点,如果,
那么 (度), 边上的高是 .
7.如图3,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条.这样做利
用的数学道理是 .
二.选择题(每小题4分,共24分)
8.下列各线段能组成一个三角形的是( )
、 、 、 、
9.一个三角形的三个内角中,至少有( )
、一个锐角 、两个锐角 、一个钝角 、一个直角
10.下列说法中错误的是( )
、三角形的一个外角大于任何一个内角
、三角形的中线、角平分线、高都是线段
、三角形按边分可分为不等边三角形和等腰三角形
、任意多边形的外角和都是
11.内角和等于外角和的多边形是( )
、三角形 、四边形 、五边形 、六边形
12.下列形状的地砖中,不能把地面铺成既无缝隙 又不重叠覆盖的地板的是( )
、正三角形 、正方形
、正五边形 、长方形
13.如图4,,是的角平分线,,则( )
、 、 、 、
三.解答题(第14题10分,其余每小题9分,共37分)
14.已知为等腰三角形,如果它的两条边的长分别为和,那么它的周长是多少?
15.一个多边形的内角和等于它的外角和的倍.求这个多边形的边数.
16.如图,已知,,求,,的度数.
17.已知:如图在中,平分,,.
求的度数.
四.探索题(每空1分,共6分)
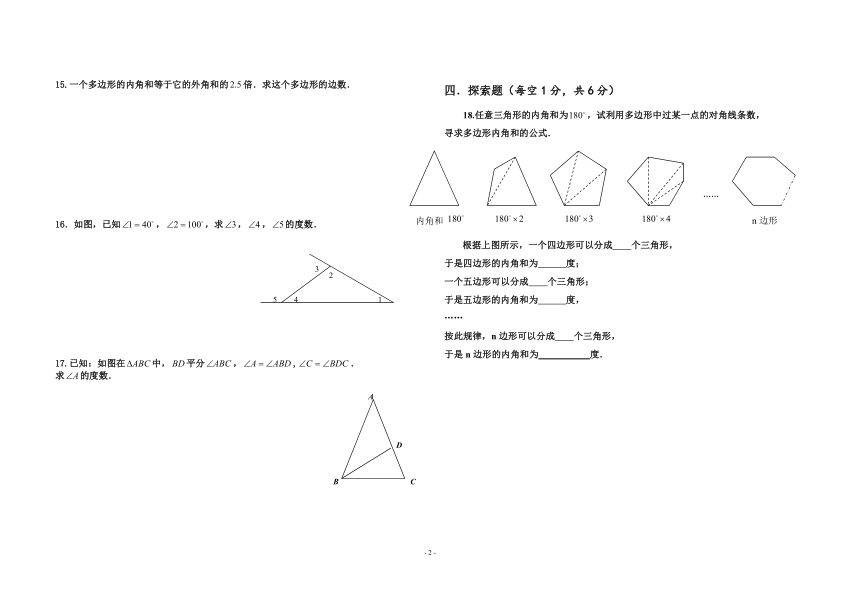
18.任意三角形的内角和为,试利用多边形中过某一点的对角线条数,
寻求多边形内角和的公式.
根据上图所示,一个四边形可以分成 个三角形,
于是四边形的内角和为 度;
一个五边形可以分成 个三角形;
于是五边形的内角和为 度,
……
按此规律,n边形可以分成 个三角形,
于是n边形的内角和为 度.
华师大版数学 第九章《多边形》单元测试
(参考答案,满分:100分)
班级 姓名 学号 成绩
一.填空题(每空3分,共33分)
1.在中,若,,则 45° .
2.两根木棒的长分别是和,要选择第三根木棒,将它们钉成三角形。
已知第三根木棒长为奇数,则第三根木棒的长度应该等于 3cm .
3.一个多边形内角和为,则这个多边形是 八 边形;
五边形中一共有 五 条对角线.
4. 三角形三个内角之比为3:2:5,则最小角等于 54 (度),
它是 直角 三角形.
5.如图1,,,,那么 65°, 40°.
6.如图2,在中,,于点,如果,
那么 30 (度), 边上的高是 BC .
7.如图3,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条.这样做利
用的数学道理是 三角形具有稳定性 .
二.选择题(每小题4分,共24分)
8.下列各线段能组成一个三角形的是( C )
、 、 、 、
9.一个三角形的三个内角中,至少有( B )
、一个锐角 、两个锐角 、一个钝角 、一个直角
10.下列说法中错误的是( A )
、三角形的一个外角大于任何一个内角
、三角形的中线、角平分线、高都是线段
、三角形按边分可分为不等边三角形和等腰三角形
、任意多边形的外角和都是
11.内角和等于外角和的多边形是( B )
、三角形 、四边形 、五边形 、六边形
12.下列形状的地砖中,不能把地面铺成既无缝隙又不重叠覆盖的地板的是( C )
、正三角形 、正方形
、正五边形 、长方形
13.如图4,,是的角平分线,,则( B )
、 、 、 、
三.解答题(第14题10分,其余每小题9分,共37分)
14.已知为等腰三角形,如果它的两条边的长分别为和,
那么它的周长是多少?
解:(1)若的腰长为8cm,则三边分别是8cm、8cm、5cm .
∵5+8>8 ∴符合题意
它的周长:8+8+5=21cm
(2)若的腰长为5cm,则三边分别是5cm、5cm、8cm .
∵5+5>8 ∴符合题意
它的周长:5+5+8=18cm
答:若的腰长为8cm,周长为21cm;
若的腰长为5cm,周长为18cm 。
15.一个多边形的内角和等于它的外角和的倍.求这个多边形的边数.
解:设这个多边形的边数为n,依题意得
答:这个多边形的边数为7。
16.如图,已知,,求,,的度数.
解:
答:
17.已知:如图在中,平分,,.
求的度数.
解:设
∵平分 ∴
又∵ ∴
答:的度数为36°。
四.探索题(每空1分,共6分)
18.任意三角形的内角和为,试利用多边形中过某一点的对角线条数,
寻求多边形内角和的公式.
根据上图所示,一个四边形可以分成 2 个三角形,
于是四边形的内角和为 360 度;
一个五边形可以分成 3 个三角形;
于是五边形的内角和为 540 度,
……
按此规律,n边形可以分成 (n-2) 个三角形,
于是n边形的内角和为 (n-2)180 度.
A
B
C
D
E
F
(图1)
(图2)
2
1
C
D
B
A
(图3)
……
内角和
n边形
3
5
4
2
1
D
B
C
A
(图4)
F
B
C
E
D
A
A
B
C
D
E
F
(图1)
(图3)
A
B
D
C
1
2
(图2)
A
D
E
C
B
F
(图4)
……
n边形
内角和
1
2
4
5
3
A
B
C
D
PAGE
- 3 -
(时间:45分钟,满分:100分)
班级 姓名 学号 成绩
一.填空题(每空3分,共33分)
1.在中,若,,则 .
2.两根木棒的长分别是和,要选择第三根木棒,将它们钉成三角形。
已知第三根木棒长为奇数,则第三根木棒的长度应该等于 .
3.一个多边形内角和为,则这个多边形是 边形;
五边形中一共有 条对角线.
4. 三角形三个内角之比为3:2:5,则最小角等于 (度),
它是 三角形.
5.如图1,,,,那么 , .
6.如图2,在中,,于点,如果,
那么 (度), 边上的高是 .
7.如图3,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条.这样做利
用的数学道理是 .
二.选择题(每小题4分,共24分)
8.下列各线段能组成一个三角形的是( )
、 、 、 、
9.一个三角形的三个内角中,至少有( )
、一个锐角 、两个锐角 、一个钝角 、一个直角
10.下列说法中错误的是( )
、三角形的一个外角大于任何一个内角
、三角形的中线、角平分线、高都是线段
、三角形按边分可分为不等边三角形和等腰三角形
、任意多边形的外角和都是
11.内角和等于外角和的多边形是( )
、三角形 、四边形 、五边形 、六边形
12.下列形状的地砖中,不能把地面铺成既无缝隙 又不重叠覆盖的地板的是( )
、正三角形 、正方形
、正五边形 、长方形
13.如图4,,是的角平分线,,则( )
、 、 、 、
三.解答题(第14题10分,其余每小题9分,共37分)
14.已知为等腰三角形,如果它的两条边的长分别为和,那么它的周长是多少?
15.一个多边形的内角和等于它的外角和的倍.求这个多边形的边数.
16.如图,已知,,求,,的度数.
17.已知:如图在中,平分,,.
求的度数.
四.探索题(每空1分,共6分)
18.任意三角形的内角和为,试利用多边形中过某一点的对角线条数,
寻求多边形内角和的公式.
根据上图所示,一个四边形可以分成 个三角形,
于是四边形的内角和为 度;
一个五边形可以分成 个三角形;
于是五边形的内角和为 度,
……
按此规律,n边形可以分成 个三角形,
于是n边形的内角和为 度.
华师大版数学 第九章《多边形》单元测试
(参考答案,满分:100分)
班级 姓名 学号 成绩
一.填空题(每空3分,共33分)
1.在中,若,,则 45° .
2.两根木棒的长分别是和,要选择第三根木棒,将它们钉成三角形。
已知第三根木棒长为奇数,则第三根木棒的长度应该等于 3cm .
3.一个多边形内角和为,则这个多边形是 八 边形;
五边形中一共有 五 条对角线.
4. 三角形三个内角之比为3:2:5,则最小角等于 54 (度),
它是 直角 三角形.
5.如图1,,,,那么 65°, 40°.
6.如图2,在中,,于点,如果,
那么 30 (度), 边上的高是 BC .
7.如图3,为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条.这样做利
用的数学道理是 三角形具有稳定性 .
二.选择题(每小题4分,共24分)
8.下列各线段能组成一个三角形的是( C )
、 、 、 、
9.一个三角形的三个内角中,至少有( B )
、一个锐角 、两个锐角 、一个钝角 、一个直角
10.下列说法中错误的是( A )
、三角形的一个外角大于任何一个内角
、三角形的中线、角平分线、高都是线段
、三角形按边分可分为不等边三角形和等腰三角形
、任意多边形的外角和都是
11.内角和等于外角和的多边形是( B )
、三角形 、四边形 、五边形 、六边形
12.下列形状的地砖中,不能把地面铺成既无缝隙又不重叠覆盖的地板的是( C )
、正三角形 、正方形
、正五边形 、长方形
13.如图4,,是的角平分线,,则( B )
、 、 、 、
三.解答题(第14题10分,其余每小题9分,共37分)
14.已知为等腰三角形,如果它的两条边的长分别为和,
那么它的周长是多少?
解:(1)若的腰长为8cm,则三边分别是8cm、8cm、5cm .
∵5+8>8 ∴符合题意
它的周长:8+8+5=21cm
(2)若的腰长为5cm,则三边分别是5cm、5cm、8cm .
∵5+5>8 ∴符合题意
它的周长:5+5+8=18cm
答:若的腰长为8cm,周长为21cm;
若的腰长为5cm,周长为18cm 。
15.一个多边形的内角和等于它的外角和的倍.求这个多边形的边数.
解:设这个多边形的边数为n,依题意得
答:这个多边形的边数为7。
16.如图,已知,,求,,的度数.
解:
答:
17.已知:如图在中,平分,,.
求的度数.
解:设
∵平分 ∴
又∵ ∴
答:的度数为36°。
四.探索题(每空1分,共6分)
18.任意三角形的内角和为,试利用多边形中过某一点的对角线条数,
寻求多边形内角和的公式.
根据上图所示,一个四边形可以分成 2 个三角形,
于是四边形的内角和为 360 度;
一个五边形可以分成 3 个三角形;
于是五边形的内角和为 540 度,
……
按此规律,n边形可以分成 (n-2) 个三角形,
于是n边形的内角和为 (n-2)180 度.
A
B
C
D
E
F
(图1)
(图2)
2
1
C
D
B
A
(图3)
……
内角和
n边形
3
5
4
2
1
D
B
C
A
(图4)
F
B
C
E
D
A
A
B
C
D
E
F
(图1)
(图3)
A
B
D
C
1
2
(图2)
A
D
E
C
B
F
(图4)
……
n边形
内角和
1
2
4
5
3
A
B
C
D
PAGE
- 3 -
