广西桂林市国龙外国语学校2023届高三下学期3月模拟预测考试理科数学试卷(PDF版含答案)
文档属性
| 名称 | 广西桂林市国龙外国语学校2023届高三下学期3月模拟预测考试理科数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 16:53:43 | ||
图片预览




文档简介
2023 桂林市国龙外国语学校高三数学 3 月预测考试理科试卷
一、选择题(本题共 12 题,每题 5 分,满分 60 分;每小题有且仅有一个选项是正确的)
1、设集合 M = {(x, y)|x2 = y}, N = {(x, y)| |y| = x},则集合 M ∩ N的真子集的个数为( )个
A. 3 B. 4 C. 7 D.15
z + z�
2、复数 z的共轭复数z�对应点的坐标为( 1,2),则 的虚部为( )zz� + i
A. 1 B. 1 C. 1 D. 1
12 12 13 13
3.下表是某生活超市 2021 年第四季度各区域营业收入占比和净利润占比统计表:
生鲜区 熟食区 乳制品区 日用品区 其它区
营业收入占比 48.6% 15.8% 20.1% 10.8% 4.7%
净利润占比 65.8% 4.3% 16.5% 20.2% 1.8%
该生活超市本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),给出下列四个结论:
①本季度此生活超市营业收入最低的是熟食区;
②本季度此生活超市的营业净利润超过一半来自生鲜区;
③本季度此生活超市营业利润率最高的是日用品区;
④本季度此生活超市生鲜区的营业利润率超过 40% . 其中正确结论的序号是( )
A.①③ B.②④ C.②③ D.②③④
4.若非零向量 a ,b 满足 a 3 b , 2a 3b b ,则 a与b 的夹角为( )
π π 2π 5π
A. B. C. D.
6 3 3 6
5.过抛物线 y2 4x的焦点 F 的直线交该抛物线于 A,B两点,O为坐标原点.若 AF 3,且 AOB 3 2的面积为 ,
2
则点 B的纵坐标为( )
1
A 2. 1 B. C. 2 D.
2 2
6.若 1 2x 5 a0 a1x a x2 a x3 a x42 3 4 a5x5,则 a1 a3 a5 ( )
A.121 B.-122 C.-121 D.122
7.净水机常采用分级过滤,其中第一级过滤一般由孔径为5微米的 PP 棉滤芯(聚丙烯熔喷滤芯)构成,其结
构是多层式,主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质.假设每一层 PP 棉滤芯可以过滤掉三
分之一的大颗粒杂质,过滤前水中大颗粒杂质含量为 25mg/L,若要满足过滤后水中大颗粒杂质含量不超
过 2.5mg/L,则 PP 棉滤芯层数最少为( )(参考数据: lg 2 0.30, lg 3 0.48)
A.5 B.6 C.7 D.8
1
8.如图所示的程序框图中,若输出的函数值 f x ,则输入的实数 x ( )
2
1
A.
2
B. 2
C 2.
2
1
D. 或
2 2
9.我国南北朝时期的科学家祖暅,提出了计算体积的祖暅原理:“幂势既同,则积不容异.”意思是:如果两个等高的几何
体,在等高处的截面积恒等,则这两个几何体的体积相等.利用此原理求以下几何体的体积:曲线 y x2 (0 y L)绕 y
轴旋转一周得几何体 Z ,将 Z 放在与 y轴垂直的水平面 上,用平行于平面 ,且与 Z 的顶点O距离为 l的平面截几何
体 Z ,得截面圆的面积为 ( l )2 l .由此构造右边的几何体 Z1:其中 AC 平
面 , AC L, AA1 , AA1 ,它与 Z 在等高处的截面面积都相等,
图中 EFPQ为矩形,且 PQ , FP l,则几何体 Z 的体积为( )
1 1
A. L2 B. L3 C. L2 D. L3
2 2
第 1 页 共 10 页
10.设 an 是等差数列,且公差不为零,其前 n项和为 Sn.则“ n N ,an 1 an ”是“ Sn 为递增数列”的( ).
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
π
11.已知函数 f (x) asin x 2 3cos x的一条对称轴为 x , f (x1) f (x2 ) 0,且函数 f (x)在 (x1, x2 )上具有单6
调性,则 | x1 x2 |的最小值为
2π π π
A. B. C
4π
. D.
3 3 6 3
12 x.若对函数 f x 2x sin x 的图象上任意一点处的切线 l1,函数 g x me m 2 x的图象上总存在一点
处的切线 l2,使得 l1 l2,则m的取值范围是( )
e e
A. ,0 B.2
0,
2
C. 1,0 D. 0,1
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
x 3
13.若 x,y满足 x y 2,则 x 2y的最大值为______.
y x
2
14 C : y x
2
.若双曲线 2 1的一条渐近线方程为 y 3x,则双曲线C的离心率为 .6 b
15.△ABC中,角 A,B,C所对的三边分别为 a,b,c,c=2b,若△ABC的面积为 1,则 BC的最小值是______.
16.已知定义在 R 上的偶函数 f x 满足 f 1 x f 1 x 4 .若 f 0 0,且 f x 在 0,1 单调递增,则满足
f (x) sin πx 2的 x的取值范围是 .
4
三、解答题(本题满分 70 分,17--21 为必答题,每题 12 分;22--23 两题为选做题,每题 10 分)
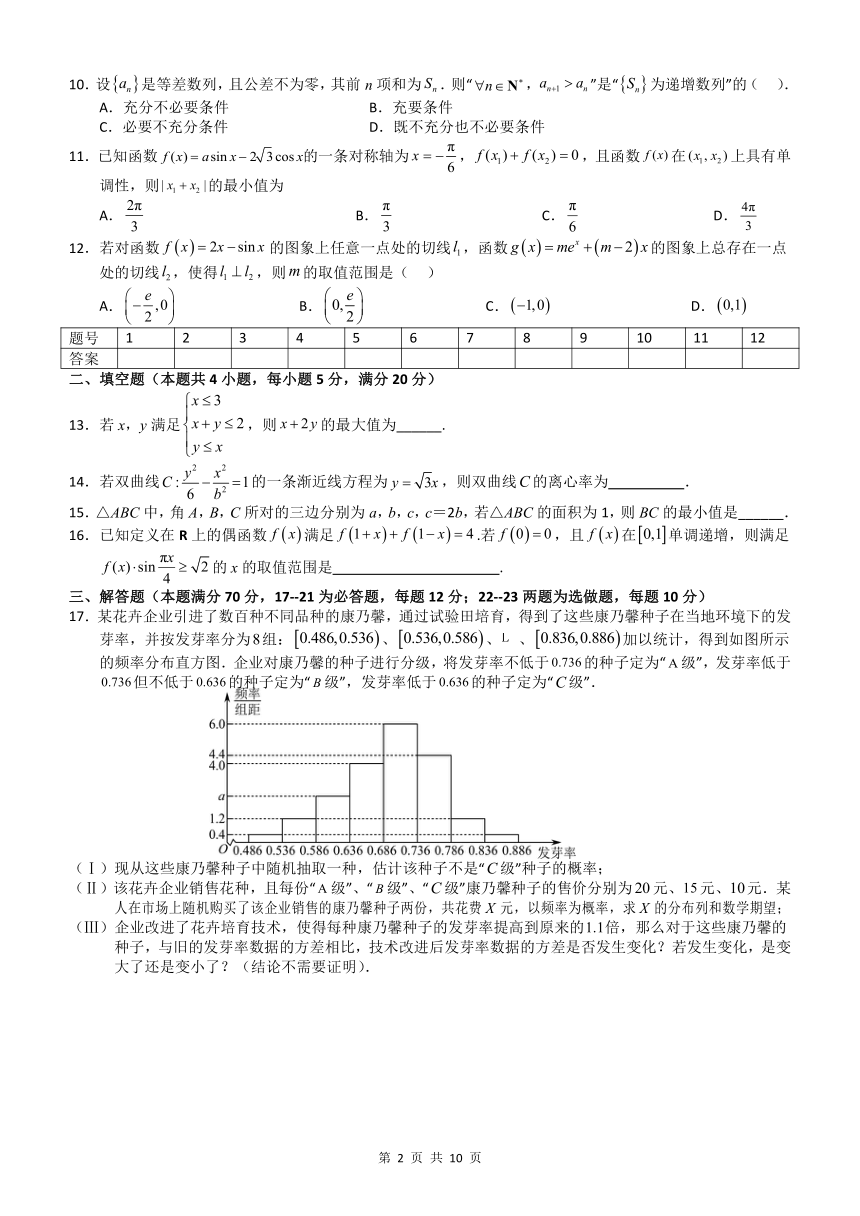
17.某花卉企业引进了数百种不同品种的康乃馨,通过试验田培育,得到了这些康乃馨种子在当地环境下的发
芽率,并按发芽率分为8组: 0.486,0.536 、 0.536,0.586 、L 、 0.836,0.886 加以统计,得到如图所示
的频率分布直方图.企业对康乃馨的种子进行分级,将发芽率不低于 0.736的种子定为“A级”,发芽率低于
0.736但不低于 0.636的种子定为“ B级”,发芽率低于 0.636的种子定为“C级”.
(Ⅰ)现从这些康乃馨种子中随机抽取一种,估计该种子不是“C级”种子的概率;
(Ⅱ)该花卉企业销售花种,且每份“A级”、“ B级”、“C级”康乃馨种子的售价分别为20元、15元、10元.某
人在市场上随机购买了该企业销售的康乃馨种子两份,共花费 X 元,以频率为概率,求 X 的分布列和数学期望;
(Ⅲ)企业改进了花卉培育技术,使得每种康乃馨种子的发芽率提高到原来的1.1倍,那么对于这些康乃馨的
种子,与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差是否发生变化?若发生变化,是变
大了还是变小了?(结论不需要证明).
第 2 页 共 10 页
18(本题 12 分)、三棱柱 ABC A1B1C1中,侧面 AA1C1C是矩形,E是 1 1的中点,且 AB = AC = 2, A1E ⊥ EC.
(1)证明:直线 AA1为异面直线 AC和A1B1的公垂线.
(2)若 AC和A1B1的距离为 4,二面角 C AA °1 B1为60 ,求直线 BA1与平面 CA1E所成角的正弦值。
19(本题 12 分)、设数列 的前 n项和为 ,且 与 4 的等差中项为 .
(1)证明:数列 + 2 是等比数列。
an + 2 1 1 1 1
(2)设bn = log3 2 ,证明: 1 + b 1 + 1 + 1 +
b
1 b3 b5 b
> 2n+1
2n 1
20.(本题 12 分)如图,已知点 F1 1,0 ,F2 1,0 ,以线段 F2G为直径的圆内切于圆O : x2 y 2 4.
(1)证明 GF1 GF2 为定值,并写出点G的轨迹 E的方程;
(2)设点 A,B,C是曲线 E上的不同三点,且OA OB OC 0,求 AOB的面积.
第 3 页 共 10 页
21 n 2 n.(本题 12 分)已知函数 f x x x cosx(其中n Z).
π
(1) n 1 f x 若 ,判断函数 在 0, 2 上的单调性;
(2)若 n 1,判断函数 f x 零点个数,并说明理由;
(3)若 n 0,求证: f x 2 x
ex 1
0
以下两题为选做题,考生只需从中选出一题解答即可
= 2 / =
22(本题 12 分)、曲线 E: = 2 , 为参数,在伸缩变换 / = 1 下曲线 E 变为曲线 C,直线 的参数方程
2
= 1 +
为 = 1 + 2 ,以坐标原点 O 为极点,x轴的正半轴为极轴,建立极坐标系,点 P的极坐标方程为 2, .4
(1)求曲线 C 的普通方程和直线 的极坐标方程。
(2)设直线 与曲线 C 交于 A、B 两点,求|PA| + |PB|的值
23(本题 10 分)、已知三个正实数 a, b, c 满足 ab + 3bc + 2ca = 4abc
1 1 1 8
(1)证明: + + ≥
a2 b2 c2 7
(2)当 c = 1 时,求|2a 1| + |2 3b|的最小值
第 4 页 共 10 页
2023桂林市国龙外国语学校高三数学 3月预测考试理科试卷
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A C D C C B B D C C A D
1 1
12 详解:由 f x 2x sin x ,得 f x 2 cos x 1,3 ,所以 1, =A,
2 cos x 3
由 g x mex m 2 x x,得 g x me m 2 .
(1)当m 0时,导函数单调递增, g x m 2, ,
由题意得 x1, x2 , f (x1)g x2 1 g x2
1
A B
f (x1)
故m 2 1,解得0 m 1;
1
(2)当m 0时,导函数单调递减, g x ,m 2 ,同理可得m 2 ,与m 0矛盾,舍去;
3
(3)当m 0时,不符合题意.
综上所述:m的取值范围为 0,1 .
二、填空题
13 2 3.3 14. 15. 3 16. 1 8k,3 8k ,k Z
3
1 1 1
15 题【详解】因为△ABC的面积为 1,所 bc sin A b 2b sin A b2 sin A 1 2,可得b ,
2 2 sin A
由 BC AC AB,可得 | BC |2 | AC |2 | AB |2 2AC AB b2 c2 2bc cos A b2
2b 2 2b 2b cos A 5b2 4b2 cos A 5 4cos A 5 4cos A ,
sin A sin A sin A
sin A 1 m sin A
设 ,其中 A (0, π),
4cos A 5 4 cos A 5
4
sin A sin A 0
因为 P
5 ,0
cos A 5 5 cos A 表示点 与点(cosA,sinA)连线的斜率, 44 4
如图所示,当过点 P的直线与半圆相切时,此时斜率最小,
在直角△OAP中,OA 1,OP
5
3,可得 PA ,
4 4
k 4所以斜率的最小值为 PA tan APO ,3
1 4 1
所以 m的最大值为 ,所以 | BC |2 3,所以 | BC | 3,即 BC的最小值为 ,4 3
3
3
故答案为: 3.
16【详解】因为 f x 是偶函数,所以 f x f x ,
由 f 1 x f 1 x 4 ,可得 f x 关于 1,2 对称,
因为 f 1 x f 1 x 4 ,所以 f 1 x 3 f 1 x 3 4,
则 f x 4 f 1 x 3 f 1 x 3 4 f x 2 4,
因为 f x 是偶函数,所以 f x 2 f x 2 ,
因为 f 1 x f 1 x 4,所以 f 1 x 1 f 1 x 1 4,
则 f x 4 f x 2 4 f 1 1 x 4 f 1 1 x f x f x ,
所以函数 f x 是周期为 4的周期函数.
因为 f x 是偶函数,且在 0,1 单调递增,所以 f x 在 1,0 单调递减,
第 5 页 共 10 页
令 f 1 x f 1 x 4 中 x 0,则 f 1 f 1 4,则 f 1 2,
又因为 f x 关于 1,2 对称,所以 f x 在 1,2 上单调递增, 2,3 上单调递减,
结合函数 f x 是周期为 4的周期函数,
综上可得 f x 在 0,2 , 4,6 上单调递增, 2,4 , 6,8 上单调递减.
y π T
2π
8 π
因为 sin x 的最小正周期为 π ,结合 y sin x 图象可知,
4 4 4
y sin π x 在 0,2 , 6,8 上单调递增,在 2,6 上单调递减,
4
令 f 1 x f 1 x 4 中 x 1,则 f 2 f 0 4,则 f 2 4,
π
当 x 1, y sin π 2 ,又 f 1 2,所以 f 1 sin 2 ,
4 2 4
x 3, y sin 3π 2当 ,又 f 3 f 1 f 1 2 3π,所以 f 3 sin 2 ,
4 2 4
所以当 x 0,8 时, f (x) πx sin 2,解得 x 1,3 .
4
π
又因为 f x 与 y sin x 均为周期函数,且 8 均为其周期,
4
πx
所以 f (x) sin 2的 x的取值范围是 1 8k,3 8k ,k Z .
4
故答案为: 1 8k,3 8k ,k Z .
三、解答题
17.(Ⅰ)0.8; (Ⅱ)分布列详见解析,数学期望为 31; (Ⅲ)方差变大了.
【详解】(Ⅰ)设事件M 为:“从这些康乃馨种子中随机抽取一种,且该种子不是“C级”种子”,
由图表,得 0.4 1.2 a 4.0 6.0 4.4 1.2 0.4 0.05 1,解得 a 2.4,
由图表,知“C级”种子的频率为 0.4 1.2 2.4 0.05 0.2,
故可估计从这些康乃馨种子中随机抽取一种,该种子是“C级”的概率为 0.2.
因为事件M 与事件“从这些康乃馨种子中随机抽取一种,且该种子是“C级”种子”为对立事件,
所以事件M 的概率P M 1 0.2 0.8;
(Ⅱ)由题意,任取一颗种子,恰好是“A级”康乃馨的概率为 4.4 1.2 0.4 0.05 0.3,
恰好是“ B级”康乃馨的概率为 4.0 6.0 0.05 0.5,
恰好是“C级”的概率为 0.4 1.2 2.4 0.05 0.2.
随机变量 X 的可能取值有 20、25、30、 35、 40,
P X 20 0.22且 0.04,P X 25 2 0.5 0.2 0.2,
P X 30 0.52 2 0.3 0.2 0.37,P X 35 0.3 0.5 2 0.3,
P X 40 0.32 0.09 .
所以 X 的分布列为:
X 20 25 30 35 40
P 0.04 0.2 0.37 0.3 0.09
故 X 的数学期望E X 20 0.04 25 0.2 30 0.37 35 0.3 40 0.09 31.
(Ⅲ)与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差变大了.
第 6 页 共 10 页
18 85.(Ⅰ)见解析; (Ⅱ)4 ;
85
【详解】(Ⅰ)在三棱柱中,AB//A1B1, AC//A1C1, AB = A1B1, AC = A1C1
又 E 为 1 1的中点,所以A1E ⊥ 1 1.
又A1E ⊥ EC, 所以 1 ⊥ 平面 B 1 1
而 1 平面 1 1
∴ A1E ⊥ B1B.
∵ A1A//B1B.
∴ A1A ⊥ A1E.
又侧面 AA1C1C是矩形,所以 1 ⊥ 1 1
1 1与A1E是平面 1 1 1内的两条相交直线,
所以A1A ⊥ 平面 A1B1C1
而 1 1 平面A1 1 1
∴ A1A ⊥ 1 1.
又A1A ⊥ AC,AC 和 A1B1都与 A1A 相交,所以直线 AA1为异面直线 AC和A1B1的公垂线.
(Ⅱ)由题知及(Ⅰ)得A1A=4,∠C1A1B1 = 60 。
取 BC 的中点为 F,则 EF ⊥ 平面A1 1 1。
取 E为坐标原点,CA1、EC1、EF 分别为 X 轴、Y 轴、Z 轴建立空间直角坐标系,如图所示。
则 E(0,0,0), A1( 3, 0, 0), B(0, 1,4), C(0,1,4)
∴ A���1�B�� = ( 3, 1,4), �E��A��1� = ( 3, 0,0), �E��C� = (0,1,4).
设平面 CA1E的法向量为� � = ( , , )
则� � ⊥ �E�A���1�, �a� ⊥ E���C�
∴ 3x = 0 x = 0
y + 4z = 0 y = 4z.
取 z = 1,得�a� = (0, 4,1)
设直线 BA1与平面 CA1E所成角为θ,则
|A����B�� �a�| 8 4 85
sinθ = |cos < �A��1�B��, �a� > | =
1 = =
|A���1�B��|| a���| 20 17 85
4 85
所以直线 BA1与平面 CA1E所成角的正弦值为 85
19.(Ⅰ)见解析; (Ⅱ)见证明;
详解(Ⅰ)依题知得 2 2 = 4
∴ 2Sn = 3an 4n.
当 n = 1 时, 1 = 4
当 n ≥ 2时,2Sn 1 = 3an 1 4n + 4
∴ 2Sn 2Sn 1 = 3an 3an 1 4.
2an = 3an 3an 1 4 an = 3an 1 + 4 an + 2 = 3 an 1 + 2
∵ a1 + 2 = 6 ≠ 0.
an + 2∴ = 3
an 1 + 2
所以,数列 + 2 是等比数列。
(Ⅱ)由(Ⅰ)得 + 2 = 6 3 1 = 2 3
a + 2
∴ b nn = log3 = n2
即证明: 1 + 1 1 + 1 1 + 1 1+ 1 > 2n + 1
1 3 5 2n 1
下面用数学归纳法证明此不等式:
第 7 页 共 10 页
(1)当 n=1 时,不等式左边=2> 2 × 1 + 1,不等式成立
(2)假设当 n = k(k ≥ 1, k ∈ N )时不等式成立,即:
1 1 1 1
1 + 1 + 1 + 1 + > 2k + 1
1 3 5 2k 1
那么,当 = + 1时,左边= 1 + 1 + 1 1 + 1 1+ 1 1 + 1 > 2k + 1 1 + 1
1 3 5 2k 1 2k+1 2k+1
要证 2k + 1 1 + 1 > 2k + 3 1 2,只要证 > 2 + 3 2 + 1 =
2k+1 2 +1 2 +3+ 2 +1
∵ k ≥ 1, ∴ 2k + 3 > 2k + 1
2 2 1
∴ < =
2 + 3 + 2 + 1 2 + 1 + 2 + 1 2 + 1
1
所以不等式 2k + 1 1 + > 2k + 3成立
2k+1
即当 = + 时不等式成立
综合(1)、(2)原不等式对一切正自然数 n 成立
2 2 3
20.(1) x y证明见解析; 1 (2)
4 3 2
【详解】(1)解:记线段 F2G的中点为H,
由于线段 F1F2 的中点为O,连接OH ,则OH //FG OH
1
1 , F1G ,2
设 H 的半径为 r, H 与 O内切于Q,连接HQ,则O,H ,Q三点共线,
如图, GF1 GF2 2 HO HF2 2 HO HQ 2 OQ 4为定值。
又 F1F2 2,
所以根据椭圆的定义可得G点轨迹是以 F1 1,0 ,F2 1,0 为焦点,实轴长为 2a 4的椭圆,
x2 y2
所以 E的方程为 1.
4 3
x2 y2
(2)解:因为 A,B,C是椭圆 1上的不同三点,
4 3
且OA OB OC 0.
①当直线 AB的斜率存在时,设 AB : y kx m m 0 ,
x2 y2 2 2 2
与椭圆方程 1联立,消去 y,整理得 3 4k x 8kmx 4m 12 0 .
4 3
2
设 A x , y B x , y x x 8km1 1 , 2 2 ,则 1 2 x x
4m 12
2 ,3 4k 1 2
,
3 4k 2
y y k x x 2m 6m所以 1 2 1 2 2 .
3 4k
因为OA OB OC 0,
8km 6m
所以OC OA OB x 1 x 2 ,y 1 y 2 ,所以C
3 4k 2
,
3 4k 2
.
x2C y
2
又点 在椭圆 1上,
4 3
3 8km
2
4 6m
2
2 2 2所以 3 4k 2
2 12 0,整理得: 3 4k 4m 3 4k 0, 3 4k
又3 4k 2 0,所以 4m2 3 4k 2.
此时 (8km)2 4 3 4k 2 4m2 12 48 m2 4k 2 3 144m2 0 ,
1 2 2
于是 S△AOB m x1 x
1
2 m x1 x2
2 4x1x
1 m 8km 4 4m 122 2 2 2 3 4k 2 3 4k 2
第 8 页 共 10 页
2 m 2 2 2 m 2 m 2 4k m m2 3 3 3 4k 2 2 9 3m2 12k 2 9m2 3 4k 4m 4m2 2
②当直线 AB的斜率不存在时,设 A x1, y1 ,B x1, y1 ,
因为OA OB OC 0 ,所以C 2x1,0 ,
C x
2 y2
因为点 在椭圆 1上,解得 x1 1 ,4 3
3 3 3 3 3 3
所以 A 1, ,B 1,
,C 2,0 A
1, ;或 ,B 1,
,C 2,0
;或 A 1, ,B 1, ,
2 2 2 2 2 2
C 2,0 ;或 A 1, 3 , B
1, 3 ,C 2,0 ,
2 2
3
此时. S AOB ,2
综上, AOB 3的面积为 .
2
π
21.(1)
函数 f x 在 0, 2 上单调递增;
(2)函数 f x 有三个零点,理由见解析;
(3)证明见解析.
1 sin x cos x π
【详解】(1)n 1时, f x x cosx , f (x) 1 2 0
在 0,
上恒成立,
x x x 2
所以函数 f x 在 0, π 2 上单调递增.
(2) n 1时, f x x 3 xcosx ,
3
令 f x x xcosx=0,所以 x 0或 x2 cos x .
令 g(x) x2 cos x, g (x) 2x sin x,
因为 g( x) x2 cos x g(x),所以函数 g(x)是偶函数.
不妨研究 x 0函数 g(x)的单调性.
当 x [0, π]时, g (x) 2x sin x 0 ,
所以函数 g(x)单调递增,
所以 g(x) x2 cos x g(0) 1,因为 g(2) 4 cos 2 0,
所以函数 g(x)在 (0, π]内有一个零点;
当x (π, )时,设h(x) 2x sin x, h (x) 2 cos x 0,
所以函数 h(x)单调递增,所以函数 g (x) 2x sin x 单调递增.
所以 g(x) x2 cos x g(π) π2 1 0,
所以函数 g(x)在 (π, )内没有零点.
根据函数的奇偶性得函数 f x 有三个零点.
综上所述,函数 f x 有三个零点.
(3) n 0时, f x x2 cosx 2,即证 x cos x 2 x 0 .
ex 1
2 x
即证 x cos x 2 .
ex 1
由(2)得 g(x) x2 cos x g(0) 1,
p(x) x 1 x设 x 1 2, p (x) x 1 ,e e
所以当 x 1时, p (x) 0, p(x) 在 (1, )单调递减;
当 x 1时, p (x) 0, p(x) 在 ( ,1)单调递增.
2 x
所以[p(x)]max p(1) 1,所以 x cos x ex 1
2 .
原题即得证
第 9 页 共 10 页
2 2
22.(1) 曲线 C: + = 1;直线 l:ρ(2cosθ sinθ) 3 = 0
4 2
(2)2 10
3
【详解】(1)曲线 E 的普通方程为 2 + 2 = 4
/ = 2 2
在伸缩变换 / = 1 下曲线 E 变为曲线 C,则曲线 C 的普通方程为 + = 1。4 2
2
直线 普通方程为 y = 2x 3
=
把 = 代入得直线 的极坐标方程为ρ(2cosθ sinθ) 3 = 0
(2)点 P 的直角坐标为 1, 1 ,所以点 P ∈
1
x = 1 + t
∴ 5直线 的参数方程化为 2 , t为参数
y = 1 + t
5
2 2
C + = 1 1 + 1
2
+ 2 1 + 2
2
代入 的普通方程 得: = 4
4 2 5 5
化简为 9t2 6 5t 5 = 0
由韦达定理得: 1 + 2 =
6 5 , 1
5
9 2
=
9
2 10
|PA| + |PB| = |t 21 t2| = t1 + t2 4t1t2 = 3
23.(1)证明见解析;(2)5
3 2 1
【详解】(1)由条件化为: + + = 4
∵ a, b, c ∈ R+,所以由柯西不等式得:
3 2 1 2 2 2 2 1 1 1+ + ≤ 3 + 2 + 1 + +
a2 b2 c2
1 1 1
当且仅当 = = 即 a = 7 , b = 7 , c = 7时上式取等号
3 2 6 4 2
1 1 1 16 8
∴ 2 + 2 + ≥ =a b c2 14 7
(2))当 c = 1 时,条件等式化为 3b + 2a = 3ab 1 + 2 = 1
3
2
∴ a > 1, b >
3
∴ |2a 1| + |2 3b| = 2a + 3b 3 = 3ab 3
由平均值不等式得:2a + 3b ≥ 2 2a 3b 3ab ≥ 2 6ab 3ab ≥ 8
4
当且仅当 2a = 3b即 a = 2, b = 时上式取等号
3
所以|2a 1| + |2 3b|的最小值为 5
第 10 页 共 10 页
一、选择题(本题共 12 题,每题 5 分,满分 60 分;每小题有且仅有一个选项是正确的)
1、设集合 M = {(x, y)|x2 = y}, N = {(x, y)| |y| = x},则集合 M ∩ N的真子集的个数为( )个
A. 3 B. 4 C. 7 D.15
z + z�
2、复数 z的共轭复数z�对应点的坐标为( 1,2),则 的虚部为( )zz� + i
A. 1 B. 1 C. 1 D. 1
12 12 13 13
3.下表是某生活超市 2021 年第四季度各区域营业收入占比和净利润占比统计表:
生鲜区 熟食区 乳制品区 日用品区 其它区
营业收入占比 48.6% 15.8% 20.1% 10.8% 4.7%
净利润占比 65.8% 4.3% 16.5% 20.2% 1.8%
该生活超市本季度的总营业利润率为32.5%(营业利润率是净利润占营业收入的百分比),给出下列四个结论:
①本季度此生活超市营业收入最低的是熟食区;
②本季度此生活超市的营业净利润超过一半来自生鲜区;
③本季度此生活超市营业利润率最高的是日用品区;
④本季度此生活超市生鲜区的营业利润率超过 40% . 其中正确结论的序号是( )
A.①③ B.②④ C.②③ D.②③④
4.若非零向量 a ,b 满足 a 3 b , 2a 3b b ,则 a与b 的夹角为( )
π π 2π 5π
A. B. C. D.
6 3 3 6
5.过抛物线 y2 4x的焦点 F 的直线交该抛物线于 A,B两点,O为坐标原点.若 AF 3,且 AOB 3 2的面积为 ,
2
则点 B的纵坐标为( )
1
A 2. 1 B. C. 2 D.
2 2
6.若 1 2x 5 a0 a1x a x2 a x3 a x42 3 4 a5x5,则 a1 a3 a5 ( )
A.121 B.-122 C.-121 D.122
7.净水机常采用分级过滤,其中第一级过滤一般由孔径为5微米的 PP 棉滤芯(聚丙烯熔喷滤芯)构成,其结
构是多层式,主要用于去除铁锈、泥沙、悬浮物等各种大颗粒杂质.假设每一层 PP 棉滤芯可以过滤掉三
分之一的大颗粒杂质,过滤前水中大颗粒杂质含量为 25mg/L,若要满足过滤后水中大颗粒杂质含量不超
过 2.5mg/L,则 PP 棉滤芯层数最少为( )(参考数据: lg 2 0.30, lg 3 0.48)
A.5 B.6 C.7 D.8
1
8.如图所示的程序框图中,若输出的函数值 f x ,则输入的实数 x ( )
2
1
A.
2
B. 2
C 2.
2
1
D. 或
2 2
9.我国南北朝时期的科学家祖暅,提出了计算体积的祖暅原理:“幂势既同,则积不容异.”意思是:如果两个等高的几何
体,在等高处的截面积恒等,则这两个几何体的体积相等.利用此原理求以下几何体的体积:曲线 y x2 (0 y L)绕 y
轴旋转一周得几何体 Z ,将 Z 放在与 y轴垂直的水平面 上,用平行于平面 ,且与 Z 的顶点O距离为 l的平面截几何
体 Z ,得截面圆的面积为 ( l )2 l .由此构造右边的几何体 Z1:其中 AC 平
面 , AC L, AA1 , AA1 ,它与 Z 在等高处的截面面积都相等,
图中 EFPQ为矩形,且 PQ , FP l,则几何体 Z 的体积为( )
1 1
A. L2 B. L3 C. L2 D. L3
2 2
第 1 页 共 10 页
10.设 an 是等差数列,且公差不为零,其前 n项和为 Sn.则“ n N ,an 1 an ”是“ Sn 为递增数列”的( ).
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
π
11.已知函数 f (x) asin x 2 3cos x的一条对称轴为 x , f (x1) f (x2 ) 0,且函数 f (x)在 (x1, x2 )上具有单6
调性,则 | x1 x2 |的最小值为
2π π π
A. B. C
4π
. D.
3 3 6 3
12 x.若对函数 f x 2x sin x 的图象上任意一点处的切线 l1,函数 g x me m 2 x的图象上总存在一点
处的切线 l2,使得 l1 l2,则m的取值范围是( )
e e
A. ,0 B.2
0,
2
C. 1,0 D. 0,1
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本题共 4 小题,每小题 5 分,满分 20 分)
x 3
13.若 x,y满足 x y 2,则 x 2y的最大值为______.
y x
2
14 C : y x
2
.若双曲线 2 1的一条渐近线方程为 y 3x,则双曲线C的离心率为 .6 b
15.△ABC中,角 A,B,C所对的三边分别为 a,b,c,c=2b,若△ABC的面积为 1,则 BC的最小值是______.
16.已知定义在 R 上的偶函数 f x 满足 f 1 x f 1 x 4 .若 f 0 0,且 f x 在 0,1 单调递增,则满足
f (x) sin πx 2的 x的取值范围是 .
4
三、解答题(本题满分 70 分,17--21 为必答题,每题 12 分;22--23 两题为选做题,每题 10 分)
17.某花卉企业引进了数百种不同品种的康乃馨,通过试验田培育,得到了这些康乃馨种子在当地环境下的发
芽率,并按发芽率分为8组: 0.486,0.536 、 0.536,0.586 、L 、 0.836,0.886 加以统计,得到如图所示
的频率分布直方图.企业对康乃馨的种子进行分级,将发芽率不低于 0.736的种子定为“A级”,发芽率低于
0.736但不低于 0.636的种子定为“ B级”,发芽率低于 0.636的种子定为“C级”.
(Ⅰ)现从这些康乃馨种子中随机抽取一种,估计该种子不是“C级”种子的概率;
(Ⅱ)该花卉企业销售花种,且每份“A级”、“ B级”、“C级”康乃馨种子的售价分别为20元、15元、10元.某
人在市场上随机购买了该企业销售的康乃馨种子两份,共花费 X 元,以频率为概率,求 X 的分布列和数学期望;
(Ⅲ)企业改进了花卉培育技术,使得每种康乃馨种子的发芽率提高到原来的1.1倍,那么对于这些康乃馨的
种子,与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差是否发生变化?若发生变化,是变
大了还是变小了?(结论不需要证明).
第 2 页 共 10 页
18(本题 12 分)、三棱柱 ABC A1B1C1中,侧面 AA1C1C是矩形,E是 1 1的中点,且 AB = AC = 2, A1E ⊥ EC.
(1)证明:直线 AA1为异面直线 AC和A1B1的公垂线.
(2)若 AC和A1B1的距离为 4,二面角 C AA °1 B1为60 ,求直线 BA1与平面 CA1E所成角的正弦值。
19(本题 12 分)、设数列 的前 n项和为 ,且 与 4 的等差中项为 .
(1)证明:数列 + 2 是等比数列。
an + 2 1 1 1 1
(2)设bn = log3 2 ,证明: 1 + b 1 + 1 + 1 +
b
1 b3 b5 b
> 2n+1
2n 1
20.(本题 12 分)如图,已知点 F1 1,0 ,F2 1,0 ,以线段 F2G为直径的圆内切于圆O : x2 y 2 4.
(1)证明 GF1 GF2 为定值,并写出点G的轨迹 E的方程;
(2)设点 A,B,C是曲线 E上的不同三点,且OA OB OC 0,求 AOB的面积.
第 3 页 共 10 页
21 n 2 n.(本题 12 分)已知函数 f x x x cosx(其中n Z).
π
(1) n 1 f x 若 ,判断函数 在 0, 2 上的单调性;
(2)若 n 1,判断函数 f x 零点个数,并说明理由;
(3)若 n 0,求证: f x 2 x
ex 1
0
以下两题为选做题,考生只需从中选出一题解答即可
= 2 / =
22(本题 12 分)、曲线 E: = 2 , 为参数,在伸缩变换 / = 1 下曲线 E 变为曲线 C,直线 的参数方程
2
= 1 +
为 = 1 + 2 ,以坐标原点 O 为极点,x轴的正半轴为极轴,建立极坐标系,点 P的极坐标方程为 2, .4
(1)求曲线 C 的普通方程和直线 的极坐标方程。
(2)设直线 与曲线 C 交于 A、B 两点,求|PA| + |PB|的值
23(本题 10 分)、已知三个正实数 a, b, c 满足 ab + 3bc + 2ca = 4abc
1 1 1 8
(1)证明: + + ≥
a2 b2 c2 7
(2)当 c = 1 时,求|2a 1| + |2 3b|的最小值
第 4 页 共 10 页
2023桂林市国龙外国语学校高三数学 3月预测考试理科试卷
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
A C D C C B B D C C A D
1 1
12 详解:由 f x 2x sin x ,得 f x 2 cos x 1,3 ,所以 1, =A,
2 cos x 3
由 g x mex m 2 x x,得 g x me m 2 .
(1)当m 0时,导函数单调递增, g x m 2, ,
由题意得 x1, x2 , f (x1)g x2 1 g x2
1
A B
f (x1)
故m 2 1,解得0 m 1;
1
(2)当m 0时,导函数单调递减, g x ,m 2 ,同理可得m 2 ,与m 0矛盾,舍去;
3
(3)当m 0时,不符合题意.
综上所述:m的取值范围为 0,1 .
二、填空题
13 2 3.3 14. 15. 3 16. 1 8k,3 8k ,k Z
3
1 1 1
15 题【详解】因为△ABC的面积为 1,所 bc sin A b 2b sin A b2 sin A 1 2,可得b ,
2 2 sin A
由 BC AC AB,可得 | BC |2 | AC |2 | AB |2 2AC AB b2 c2 2bc cos A b2
2b 2 2b 2b cos A 5b2 4b2 cos A 5 4cos A 5 4cos A ,
sin A sin A sin A
sin A 1 m sin A
设 ,其中 A (0, π),
4cos A 5 4 cos A 5
4
sin A sin A 0
因为 P
5 ,0
cos A 5 5 cos A 表示点 与点(cosA,sinA)连线的斜率, 44 4
如图所示,当过点 P的直线与半圆相切时,此时斜率最小,
在直角△OAP中,OA 1,OP
5
3,可得 PA ,
4 4
k 4所以斜率的最小值为 PA tan APO ,3
1 4 1
所以 m的最大值为 ,所以 | BC |2 3,所以 | BC | 3,即 BC的最小值为 ,4 3
3
3
故答案为: 3.
16【详解】因为 f x 是偶函数,所以 f x f x ,
由 f 1 x f 1 x 4 ,可得 f x 关于 1,2 对称,
因为 f 1 x f 1 x 4 ,所以 f 1 x 3 f 1 x 3 4,
则 f x 4 f 1 x 3 f 1 x 3 4 f x 2 4,
因为 f x 是偶函数,所以 f x 2 f x 2 ,
因为 f 1 x f 1 x 4,所以 f 1 x 1 f 1 x 1 4,
则 f x 4 f x 2 4 f 1 1 x 4 f 1 1 x f x f x ,
所以函数 f x 是周期为 4的周期函数.
因为 f x 是偶函数,且在 0,1 单调递增,所以 f x 在 1,0 单调递减,
第 5 页 共 10 页
令 f 1 x f 1 x 4 中 x 0,则 f 1 f 1 4,则 f 1 2,
又因为 f x 关于 1,2 对称,所以 f x 在 1,2 上单调递增, 2,3 上单调递减,
结合函数 f x 是周期为 4的周期函数,
综上可得 f x 在 0,2 , 4,6 上单调递增, 2,4 , 6,8 上单调递减.
y π T
2π
8 π
因为 sin x 的最小正周期为 π ,结合 y sin x 图象可知,
4 4 4
y sin π x 在 0,2 , 6,8 上单调递增,在 2,6 上单调递减,
4
令 f 1 x f 1 x 4 中 x 1,则 f 2 f 0 4,则 f 2 4,
π
当 x 1, y sin π 2 ,又 f 1 2,所以 f 1 sin 2 ,
4 2 4
x 3, y sin 3π 2当 ,又 f 3 f 1 f 1 2 3π,所以 f 3 sin 2 ,
4 2 4
所以当 x 0,8 时, f (x) πx sin 2,解得 x 1,3 .
4
π
又因为 f x 与 y sin x 均为周期函数,且 8 均为其周期,
4
πx
所以 f (x) sin 2的 x的取值范围是 1 8k,3 8k ,k Z .
4
故答案为: 1 8k,3 8k ,k Z .
三、解答题
17.(Ⅰ)0.8; (Ⅱ)分布列详见解析,数学期望为 31; (Ⅲ)方差变大了.
【详解】(Ⅰ)设事件M 为:“从这些康乃馨种子中随机抽取一种,且该种子不是“C级”种子”,
由图表,得 0.4 1.2 a 4.0 6.0 4.4 1.2 0.4 0.05 1,解得 a 2.4,
由图表,知“C级”种子的频率为 0.4 1.2 2.4 0.05 0.2,
故可估计从这些康乃馨种子中随机抽取一种,该种子是“C级”的概率为 0.2.
因为事件M 与事件“从这些康乃馨种子中随机抽取一种,且该种子是“C级”种子”为对立事件,
所以事件M 的概率P M 1 0.2 0.8;
(Ⅱ)由题意,任取一颗种子,恰好是“A级”康乃馨的概率为 4.4 1.2 0.4 0.05 0.3,
恰好是“ B级”康乃馨的概率为 4.0 6.0 0.05 0.5,
恰好是“C级”的概率为 0.4 1.2 2.4 0.05 0.2.
随机变量 X 的可能取值有 20、25、30、 35、 40,
P X 20 0.22且 0.04,P X 25 2 0.5 0.2 0.2,
P X 30 0.52 2 0.3 0.2 0.37,P X 35 0.3 0.5 2 0.3,
P X 40 0.32 0.09 .
所以 X 的分布列为:
X 20 25 30 35 40
P 0.04 0.2 0.37 0.3 0.09
故 X 的数学期望E X 20 0.04 25 0.2 30 0.37 35 0.3 40 0.09 31.
(Ⅲ)与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差变大了.
第 6 页 共 10 页
18 85.(Ⅰ)见解析; (Ⅱ)4 ;
85
【详解】(Ⅰ)在三棱柱中,AB//A1B1, AC//A1C1, AB = A1B1, AC = A1C1
又 E 为 1 1的中点,所以A1E ⊥ 1 1.
又A1E ⊥ EC, 所以 1 ⊥ 平面 B 1 1
而 1 平面 1 1
∴ A1E ⊥ B1B.
∵ A1A//B1B.
∴ A1A ⊥ A1E.
又侧面 AA1C1C是矩形,所以 1 ⊥ 1 1
1 1与A1E是平面 1 1 1内的两条相交直线,
所以A1A ⊥ 平面 A1B1C1
而 1 1 平面A1 1 1
∴ A1A ⊥ 1 1.
又A1A ⊥ AC,AC 和 A1B1都与 A1A 相交,所以直线 AA1为异面直线 AC和A1B1的公垂线.
(Ⅱ)由题知及(Ⅰ)得A1A=4,∠C1A1B1 = 60 。
取 BC 的中点为 F,则 EF ⊥ 平面A1 1 1。
取 E为坐标原点,CA1、EC1、EF 分别为 X 轴、Y 轴、Z 轴建立空间直角坐标系,如图所示。
则 E(0,0,0), A1( 3, 0, 0), B(0, 1,4), C(0,1,4)
∴ A���1�B�� = ( 3, 1,4), �E��A��1� = ( 3, 0,0), �E��C� = (0,1,4).
设平面 CA1E的法向量为� � = ( , , )
则� � ⊥ �E�A���1�, �a� ⊥ E���C�
∴ 3x = 0 x = 0
y + 4z = 0 y = 4z.
取 z = 1,得�a� = (0, 4,1)
设直线 BA1与平面 CA1E所成角为θ,则
|A����B�� �a�| 8 4 85
sinθ = |cos < �A��1�B��, �a� > | =
1 = =
|A���1�B��|| a���| 20 17 85
4 85
所以直线 BA1与平面 CA1E所成角的正弦值为 85
19.(Ⅰ)见解析; (Ⅱ)见证明;
详解(Ⅰ)依题知得 2 2 = 4
∴ 2Sn = 3an 4n.
当 n = 1 时, 1 = 4
当 n ≥ 2时,2Sn 1 = 3an 1 4n + 4
∴ 2Sn 2Sn 1 = 3an 3an 1 4.
2an = 3an 3an 1 4 an = 3an 1 + 4 an + 2 = 3 an 1 + 2
∵ a1 + 2 = 6 ≠ 0.
an + 2∴ = 3
an 1 + 2
所以,数列 + 2 是等比数列。
(Ⅱ)由(Ⅰ)得 + 2 = 6 3 1 = 2 3
a + 2
∴ b nn = log3 = n2
即证明: 1 + 1 1 + 1 1 + 1 1+ 1 > 2n + 1
1 3 5 2n 1
下面用数学归纳法证明此不等式:
第 7 页 共 10 页
(1)当 n=1 时,不等式左边=2> 2 × 1 + 1,不等式成立
(2)假设当 n = k(k ≥ 1, k ∈ N )时不等式成立,即:
1 1 1 1
1 + 1 + 1 + 1 + > 2k + 1
1 3 5 2k 1
那么,当 = + 1时,左边= 1 + 1 + 1 1 + 1 1+ 1 1 + 1 > 2k + 1 1 + 1
1 3 5 2k 1 2k+1 2k+1
要证 2k + 1 1 + 1 > 2k + 3 1 2,只要证 > 2 + 3 2 + 1 =
2k+1 2 +1 2 +3+ 2 +1
∵ k ≥ 1, ∴ 2k + 3 > 2k + 1
2 2 1
∴ < =
2 + 3 + 2 + 1 2 + 1 + 2 + 1 2 + 1
1
所以不等式 2k + 1 1 + > 2k + 3成立
2k+1
即当 = + 时不等式成立
综合(1)、(2)原不等式对一切正自然数 n 成立
2 2 3
20.(1) x y证明见解析; 1 (2)
4 3 2
【详解】(1)解:记线段 F2G的中点为H,
由于线段 F1F2 的中点为O,连接OH ,则OH //FG OH
1
1 , F1G ,2
设 H 的半径为 r, H 与 O内切于Q,连接HQ,则O,H ,Q三点共线,
如图, GF1 GF2 2 HO HF2 2 HO HQ 2 OQ 4为定值。
又 F1F2 2,
所以根据椭圆的定义可得G点轨迹是以 F1 1,0 ,F2 1,0 为焦点,实轴长为 2a 4的椭圆,
x2 y2
所以 E的方程为 1.
4 3
x2 y2
(2)解:因为 A,B,C是椭圆 1上的不同三点,
4 3
且OA OB OC 0.
①当直线 AB的斜率存在时,设 AB : y kx m m 0 ,
x2 y2 2 2 2
与椭圆方程 1联立,消去 y,整理得 3 4k x 8kmx 4m 12 0 .
4 3
2
设 A x , y B x , y x x 8km1 1 , 2 2 ,则 1 2 x x
4m 12
2 ,3 4k 1 2
,
3 4k 2
y y k x x 2m 6m所以 1 2 1 2 2 .
3 4k
因为OA OB OC 0,
8km 6m
所以OC OA OB x 1 x 2 ,y 1 y 2 ,所以C
3 4k 2
,
3 4k 2
.
x2C y
2
又点 在椭圆 1上,
4 3
3 8km
2
4 6m
2
2 2 2所以 3 4k 2
2 12 0,整理得: 3 4k 4m 3 4k 0, 3 4k
又3 4k 2 0,所以 4m2 3 4k 2.
此时 (8km)2 4 3 4k 2 4m2 12 48 m2 4k 2 3 144m2 0 ,
1 2 2
于是 S△AOB m x1 x
1
2 m x1 x2
2 4x1x
1 m 8km 4 4m 122 2 2 2 3 4k 2 3 4k 2
第 8 页 共 10 页
2 m 2 2 2 m 2 m 2 4k m m2 3 3 3 4k 2 2 9 3m2 12k 2 9m2 3 4k 4m 4m2 2
②当直线 AB的斜率不存在时,设 A x1, y1 ,B x1, y1 ,
因为OA OB OC 0 ,所以C 2x1,0 ,
C x
2 y2
因为点 在椭圆 1上,解得 x1 1 ,4 3
3 3 3 3 3 3
所以 A 1, ,B 1,
,C 2,0 A
1, ;或 ,B 1,
,C 2,0
;或 A 1, ,B 1, ,
2 2 2 2 2 2
C 2,0 ;或 A 1, 3 , B
1, 3 ,C 2,0 ,
2 2
3
此时. S AOB ,2
综上, AOB 3的面积为 .
2
π
21.(1)
函数 f x 在 0, 2 上单调递增;
(2)函数 f x 有三个零点,理由见解析;
(3)证明见解析.
1 sin x cos x π
【详解】(1)n 1时, f x x cosx , f (x) 1 2 0
在 0,
上恒成立,
x x x 2
所以函数 f x 在 0, π 2 上单调递增.
(2) n 1时, f x x 3 xcosx ,
3
令 f x x xcosx=0,所以 x 0或 x2 cos x .
令 g(x) x2 cos x, g (x) 2x sin x,
因为 g( x) x2 cos x g(x),所以函数 g(x)是偶函数.
不妨研究 x 0函数 g(x)的单调性.
当 x [0, π]时, g (x) 2x sin x 0 ,
所以函数 g(x)单调递增,
所以 g(x) x2 cos x g(0) 1,因为 g(2) 4 cos 2 0,
所以函数 g(x)在 (0, π]内有一个零点;
当x (π, )时,设h(x) 2x sin x, h (x) 2 cos x 0,
所以函数 h(x)单调递增,所以函数 g (x) 2x sin x 单调递增.
所以 g(x) x2 cos x g(π) π2 1 0,
所以函数 g(x)在 (π, )内没有零点.
根据函数的奇偶性得函数 f x 有三个零点.
综上所述,函数 f x 有三个零点.
(3) n 0时, f x x2 cosx 2,即证 x cos x 2 x 0 .
ex 1
2 x
即证 x cos x 2 .
ex 1
由(2)得 g(x) x2 cos x g(0) 1,
p(x) x 1 x设 x 1 2, p (x) x 1 ,e e
所以当 x 1时, p (x) 0, p(x) 在 (1, )单调递减;
当 x 1时, p (x) 0, p(x) 在 ( ,1)单调递增.
2 x
所以[p(x)]max p(1) 1,所以 x cos x ex 1
2 .
原题即得证
第 9 页 共 10 页
2 2
22.(1) 曲线 C: + = 1;直线 l:ρ(2cosθ sinθ) 3 = 0
4 2
(2)2 10
3
【详解】(1)曲线 E 的普通方程为 2 + 2 = 4
/ = 2 2
在伸缩变换 / = 1 下曲线 E 变为曲线 C,则曲线 C 的普通方程为 + = 1。4 2
2
直线 普通方程为 y = 2x 3
=
把 = 代入得直线 的极坐标方程为ρ(2cosθ sinθ) 3 = 0
(2)点 P 的直角坐标为 1, 1 ,所以点 P ∈
1
x = 1 + t
∴ 5直线 的参数方程化为 2 , t为参数
y = 1 + t
5
2 2
C + = 1 1 + 1
2
+ 2 1 + 2
2
代入 的普通方程 得: = 4
4 2 5 5
化简为 9t2 6 5t 5 = 0
由韦达定理得: 1 + 2 =
6 5 , 1
5
9 2
=
9
2 10
|PA| + |PB| = |t 21 t2| = t1 + t2 4t1t2 = 3
23.(1)证明见解析;(2)5
3 2 1
【详解】(1)由条件化为: + + = 4
∵ a, b, c ∈ R+,所以由柯西不等式得:
3 2 1 2 2 2 2 1 1 1+ + ≤ 3 + 2 + 1 + +
a2 b2 c2
1 1 1
当且仅当 = = 即 a = 7 , b = 7 , c = 7时上式取等号
3 2 6 4 2
1 1 1 16 8
∴ 2 + 2 + ≥ =a b c2 14 7
(2))当 c = 1 时,条件等式化为 3b + 2a = 3ab 1 + 2 = 1
3
2
∴ a > 1, b >
3
∴ |2a 1| + |2 3b| = 2a + 3b 3 = 3ab 3
由平均值不等式得:2a + 3b ≥ 2 2a 3b 3ab ≥ 2 6ab 3ab ≥ 8
4
当且仅当 2a = 3b即 a = 2, b = 时上式取等号
3
所以|2a 1| + |2 3b|的最小值为 5
第 10 页 共 10 页
同课章节目录
