人教版八年级上册数学13.1.2 线段的垂直平分线的性质 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级上册数学13.1.2 线段的垂直平分线的性质 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 14:51:35 | ||
图片预览


文档简介
(共16张PPT)
13.1.2 线段的垂直平分线的性质
导入新知
罗田高铁对接选址正在进行
根据《湖北省“十四五”铁路发展规划》,修建武汉经罗田、英山至安庆高铁是支撑长江经济带和皖江城市带发展等国家战略,建立现代化高质量综合立体交通网,完善中部地区铁路网,构建武汉至杭州快递铁路通道的重要举措。铁路建成后将促进罗田、英山等革命老区交通协调发展,促进沿线地区旅游资源开发,巩固脱贫攻坚成果同乡村振兴有效衔接。
探究新知
线段的垂直平分线的性质定理
知识点 1
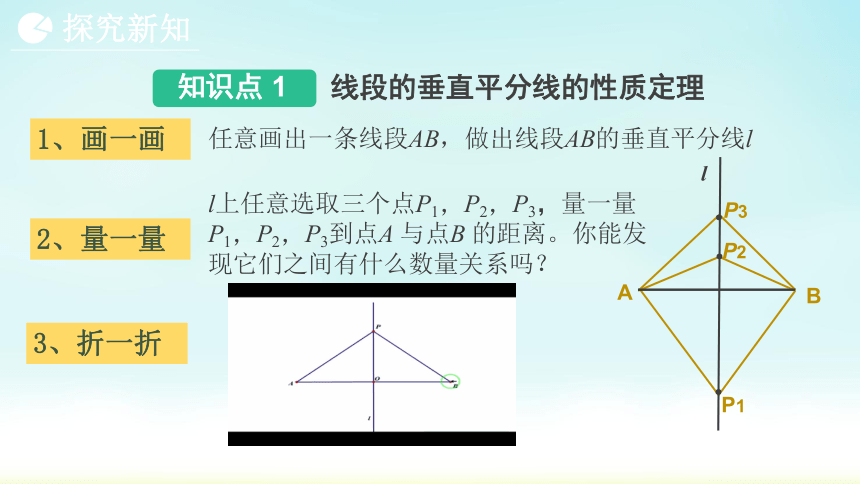
1、画一画
任意画出一条线段AB,做出线段AB的垂直平分线l
2、量一量
l上任意选取三个点P1,P2,P3,量一量P1,P2,P3到点A 与点B 的距离。你能发现它们之间有什么数量关系吗?
3、折一折
l
A
B
P3
P2
P1
·
·
·
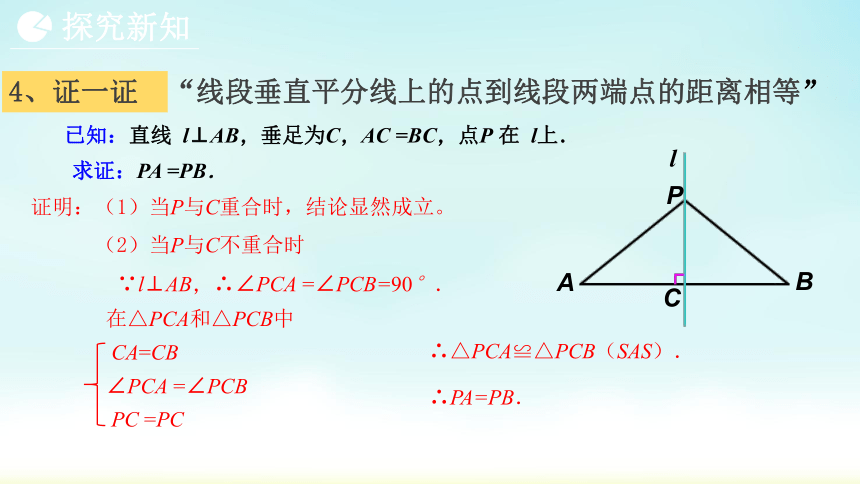
“线段垂直平分线上的点到线段两端点的距离相等”
已知:直线 l⊥AB,垂足为C,AC =BC,点P 在 l上.
求证:PA =PB.
A
B
P
C
l
探究新知
4、证一证
证明:(1)当P与C重合时,结论显然成立。
(2)当P与C不重合时
∵l⊥AB,∴∠PCA =∠PCB=90°.
在△PCA和△PCB中
CA=CB
∠PCA =∠PCB
PC =PC
∴△PCA≌△PCB(SAS).
∴PA=PB.
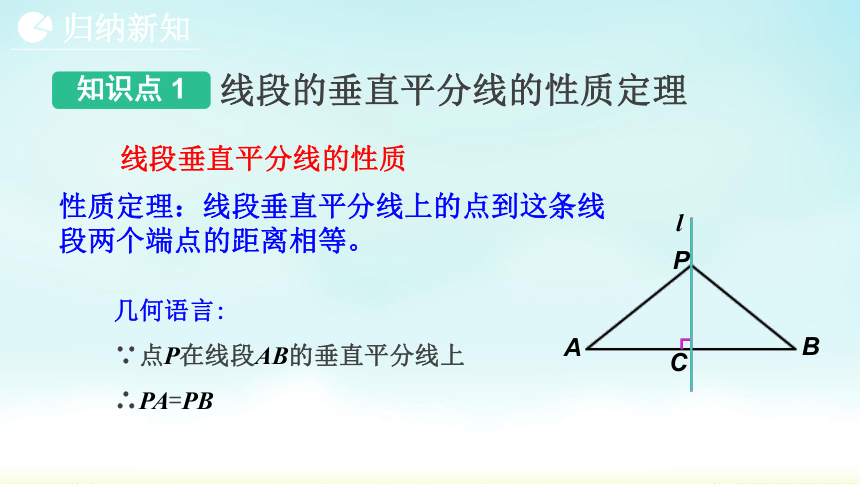
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
几何语言:
∵点P在线段AB的垂直平分线上
∴PA=PB
A
B
P
C
l
归纳新知
线段的垂直平分线的性质定理
知识点 1
线段垂直平分线的性质
应用新知
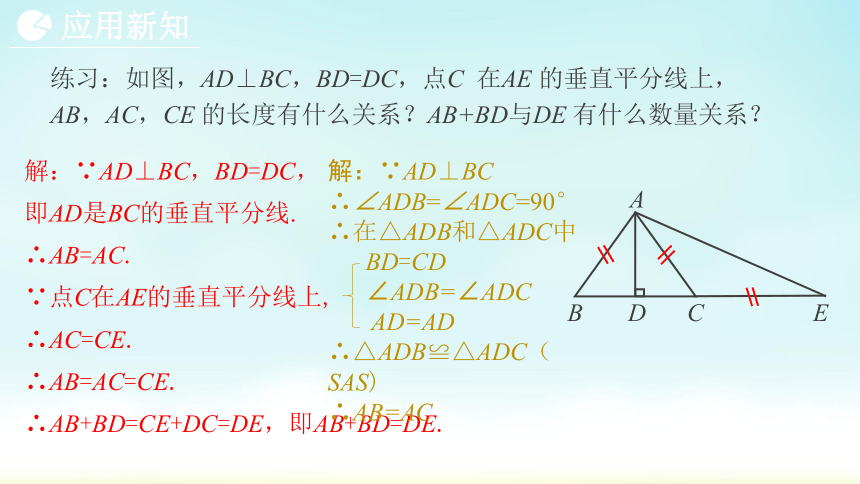
练习:如图,AD⊥BC,BD=DC,点C 在AE 的垂直平分线上,
AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么数量关系?
A
B
C
D
E
解:∵AD⊥BC,BD=DC,
即AD是BC的垂直平分线.
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE.
∴AB+BD=CE+DC=DE,即AB+BD=DE.
解:∵AD⊥BC ∴∠ADB=∠ADC=90°
∴在△ADB和△ADC中
BD=CD
∠ADB=∠ADC
AD=AD
∴△ADB≌△ADC(SAS)
∴AB=AC
小试牛刀
如图,在△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AG于点G。求证:BF=CG。
证明:连接BE,CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AG
∴EF=EG
∵DE垂直平分BC,∴EB=EC
在Rt△EFB和Rt△EGC中,
EF=EG
EB=EC
∴Rt△EFB≌Rt△EGC(HL)
∴BF=CG
动脑两分钟,解题更轻松
线段垂直平分线,
常向两端把线连.
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
已知:PA =PB.
求证:点P 在线段AB 的垂直平分线上.
探究新知
探索并证明线段垂直平分线的判定
P
A
B
探究新知
已知:PA =PB.
求证:点P 在线段AB 的垂直平分线上.
C
P
A
B
证明:(1)当点P在线段AB上时,结论显然成立.
(2)当点P不在线段AB上时,
过点P 作PC⊥AB 于点C,则∠PCA =∠PCB=90°.
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC 又PC⊥AB,
∴点P 在线段AB的垂直平分线上.
在Rt△PCA和Rt△PCB中,
PA=PB
PC=PC
你还有其他的证明方法吗?
几何语言:
∵PA =PB
∴点P在AB的垂直平分线上.
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
P
A
B
C
线段的垂直平分线的判定定理
知识点 2
归纳新知
∟
在线段AB的垂直平分线l上的点与A、B的距离都相等;
反过来,与A、B距离相等的点都在l上。
所以,直线l可以看成与两点A、B的距离相等的所有点的集合
P
A
B
C
l
∟
归纳新知
解:∵AB=AC,
∴点A在BC的垂直平分线.
∵MB=MC,
∴点M在BC的垂直平分线上
∴直线AM是线段BC的垂直平分线.
如图,AB=AC,MB=MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
应用新知
例2 尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
作法:(1)任意取一点K,使点K和点C在AB
的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于 DE 的长为半径作弧,两弧相交于点F.
F
D
E
A
B
C
应用新知
∟
∟
线段的垂直平分线
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线判定
线段垂直平分线性质
辅助线作法:线段垂直平分线,常向两端把线连.
课堂小结
观察生活,发现数学,应用数学.
13.1.2 线段的垂直平分线的性质
导入新知
罗田高铁对接选址正在进行
根据《湖北省“十四五”铁路发展规划》,修建武汉经罗田、英山至安庆高铁是支撑长江经济带和皖江城市带发展等国家战略,建立现代化高质量综合立体交通网,完善中部地区铁路网,构建武汉至杭州快递铁路通道的重要举措。铁路建成后将促进罗田、英山等革命老区交通协调发展,促进沿线地区旅游资源开发,巩固脱贫攻坚成果同乡村振兴有效衔接。
探究新知
线段的垂直平分线的性质定理
知识点 1
1、画一画
任意画出一条线段AB,做出线段AB的垂直平分线l
2、量一量
l上任意选取三个点P1,P2,P3,量一量P1,P2,P3到点A 与点B 的距离。你能发现它们之间有什么数量关系吗?
3、折一折
l
A
B
P3
P2
P1
·
·
·
“线段垂直平分线上的点到线段两端点的距离相等”
已知:直线 l⊥AB,垂足为C,AC =BC,点P 在 l上.
求证:PA =PB.
A
B
P
C
l
探究新知
4、证一证
证明:(1)当P与C重合时,结论显然成立。
(2)当P与C不重合时
∵l⊥AB,∴∠PCA =∠PCB=90°.
在△PCA和△PCB中
CA=CB
∠PCA =∠PCB
PC =PC
∴△PCA≌△PCB(SAS).
∴PA=PB.
性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等。
几何语言:
∵点P在线段AB的垂直平分线上
∴PA=PB
A
B
P
C
l
归纳新知
线段的垂直平分线的性质定理
知识点 1
线段垂直平分线的性质
应用新知
练习:如图,AD⊥BC,BD=DC,点C 在AE 的垂直平分线上,
AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么数量关系?
A
B
C
D
E
解:∵AD⊥BC,BD=DC,
即AD是BC的垂直平分线.
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE.
∴AB+BD=CE+DC=DE,即AB+BD=DE.
解:∵AD⊥BC ∴∠ADB=∠ADC=90°
∴在△ADB和△ADC中
BD=CD
∠ADB=∠ADC
AD=AD
∴△ADB≌△ADC(SAS)
∴AB=AC
小试牛刀
如图,在△ABC中,BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AG于点G。求证:BF=CG。
证明:连接BE,CE.
∵AE平分∠BAC,EF⊥AB,EG⊥AG
∴EF=EG
∵DE垂直平分BC,∴EB=EC
在Rt△EFB和Rt△EGC中,
EF=EG
EB=EC
∴Rt△EFB≌Rt△EGC(HL)
∴BF=CG
动脑两分钟,解题更轻松
线段垂直平分线,
常向两端把线连.
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
已知:PA =PB.
求证:点P 在线段AB 的垂直平分线上.
探究新知
探索并证明线段垂直平分线的判定
P
A
B
探究新知
已知:PA =PB.
求证:点P 在线段AB 的垂直平分线上.
C
P
A
B
证明:(1)当点P在线段AB上时,结论显然成立.
(2)当点P不在线段AB上时,
过点P 作PC⊥AB 于点C,则∠PCA =∠PCB=90°.
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC 又PC⊥AB,
∴点P 在线段AB的垂直平分线上.
在Rt△PCA和Rt△PCB中,
PA=PB
PC=PC
你还有其他的证明方法吗?
几何语言:
∵PA =PB
∴点P在AB的垂直平分线上.
线段垂直平分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
P
A
B
C
线段的垂直平分线的判定定理
知识点 2
归纳新知
∟
在线段AB的垂直平分线l上的点与A、B的距离都相等;
反过来,与A、B距离相等的点都在l上。
所以,直线l可以看成与两点A、B的距离相等的所有点的集合
P
A
B
C
l
∟
归纳新知
解:∵AB=AC,
∴点A在BC的垂直平分线.
∵MB=MC,
∴点M在BC的垂直平分线上
∴直线AM是线段BC的垂直平分线.
如图,AB=AC,MB=MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
应用新知
例2 尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
作法:(1)任意取一点K,使点K和点C在AB
的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于 DE 的长为半径作弧,两弧相交于点F.
F
D
E
A
B
C
应用新知
∟
∟
线段的垂直平分线
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线判定
线段垂直平分线性质
辅助线作法:线段垂直平分线,常向两端把线连.
课堂小结
观察生活,发现数学,应用数学.
