人教版八年级下册数学《平行四边形》教学设计
文档属性
| 名称 | 人教版八年级下册数学《平行四边形》教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 14:52:58 | ||
图片预览

文档简介
18.1.1平行四边形的性质
【教学目标】
一、理解平行四边形的概念.
二、探索并掌握平行四边形的对边相等、对角相等的性质.
三、初步体会几何探究的一般思路与方法.
【重点难点】
重点:平行四边形边、角的性质探索与证明.
难点:平行四边形性质的灵活应用.
【教学过程】
创设情景,导入新课
问题1 观察下列图片,它们是否都有平行四边形的形象?
由课件动画演示平行四边形,引入课题,归纳平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形.
二、观察归纳,学习新知
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
类比三角形表示方法表示出平行四边形以及几何语言表示方法.
思考:组成平行四边形的基本元素有哪些?
思考:平行四边形和四边形的联系是什么?
针对训练一
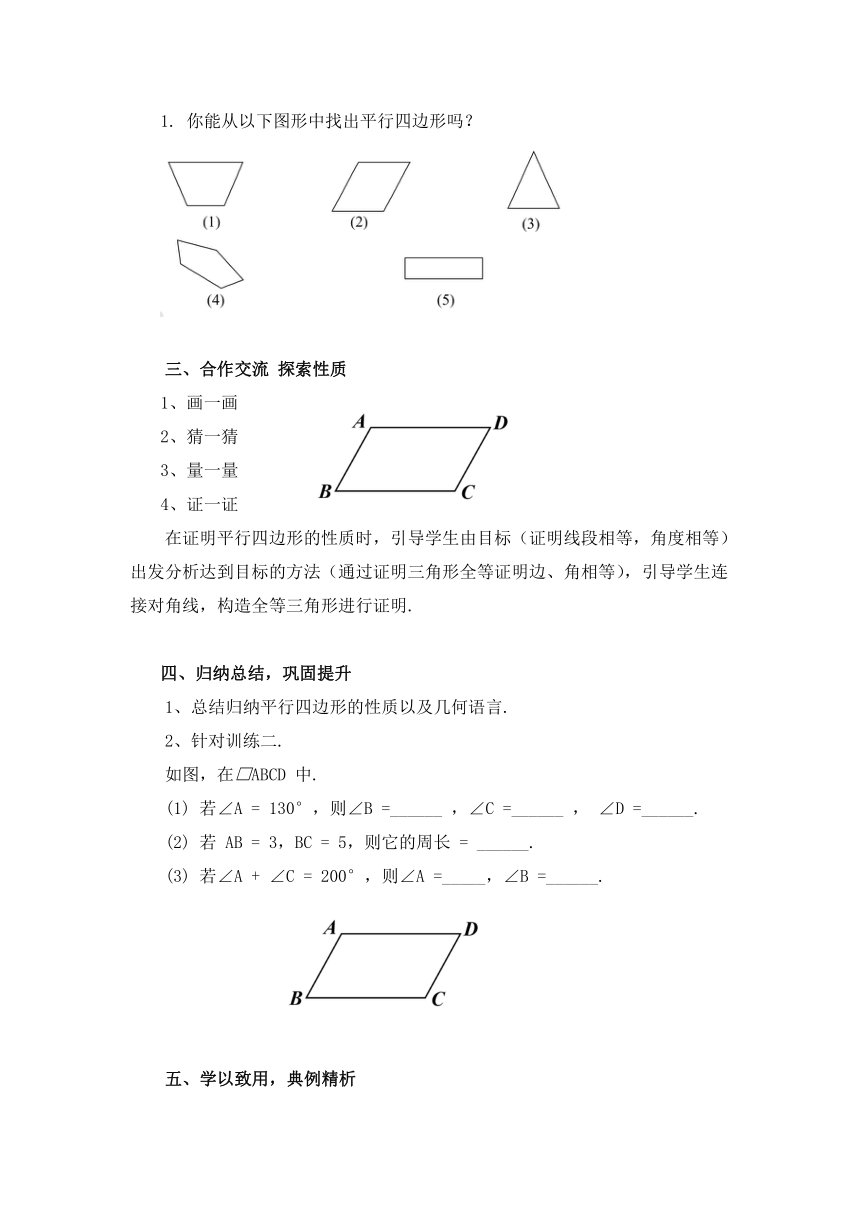
1. 你能从以下图形中找出平行四边形吗?
三、合作交流 探索性质
1、画一画
2、猜一猜
3、量一量
4、证一证
在证明平行四边形的性质时,引导学生由目标(证明线段相等,角度相等)出发分析达到目标的方法(通过证明三角形全等证明边、角相等),引导学生连接对角线,构造全等三角形进行证明.
四、归纳总结,巩固提升
1、总结归纳平行四边形的性质以及几何语言.
2、针对训练二.
如图,在ABCD 中.
(1) 若∠A = 130°,则∠B =______ ,∠C =______ , ∠D =______.
(2) 若 AB = 3,BC = 5,则它的周长 = ______.
(3) 若∠A + ∠C = 200°,则∠A =_____,∠B =______.
五、学以致用,典例精析
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE = CF.
例2 直线a∥b,A,C是直线a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?为什么?
针对训练三
已知直线 a∥b,点M到直线 a 的距离是6cm,到直线 b 的距离是3cm,那
么直线 a 和直线 b之间的距离为 ____________.
当堂小结,理顺新知
你今天学到了什么知识?
拓展训练,深化理解
△ABC是等腰三角形,AB=AC,P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上,求证:PE+PF=AB.
八、板书设计
【教学目标】
一、理解平行四边形的概念.
二、探索并掌握平行四边形的对边相等、对角相等的性质.
三、初步体会几何探究的一般思路与方法.
【重点难点】
重点:平行四边形边、角的性质探索与证明.
难点:平行四边形性质的灵活应用.
【教学过程】
创设情景,导入新课
问题1 观察下列图片,它们是否都有平行四边形的形象?
由课件动画演示平行四边形,引入课题,归纳平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形.
二、观察归纳,学习新知
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
类比三角形表示方法表示出平行四边形以及几何语言表示方法.
思考:组成平行四边形的基本元素有哪些?
思考:平行四边形和四边形的联系是什么?
针对训练一
1. 你能从以下图形中找出平行四边形吗?
三、合作交流 探索性质
1、画一画
2、猜一猜
3、量一量
4、证一证
在证明平行四边形的性质时,引导学生由目标(证明线段相等,角度相等)出发分析达到目标的方法(通过证明三角形全等证明边、角相等),引导学生连接对角线,构造全等三角形进行证明.
四、归纳总结,巩固提升
1、总结归纳平行四边形的性质以及几何语言.
2、针对训练二.
如图,在ABCD 中.
(1) 若∠A = 130°,则∠B =______ ,∠C =______ , ∠D =______.
(2) 若 AB = 3,BC = 5,则它的周长 = ______.
(3) 若∠A + ∠C = 200°,则∠A =_____,∠B =______.
五、学以致用,典例精析
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE = CF.
例2 直线a∥b,A,C是直线a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?为什么?
针对训练三
已知直线 a∥b,点M到直线 a 的距离是6cm,到直线 b 的距离是3cm,那
么直线 a 和直线 b之间的距离为 ____________.
当堂小结,理顺新知
你今天学到了什么知识?
拓展训练,深化理解
△ABC是等腰三角形,AB=AC,P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上,求证:PE+PF=AB.
八、板书设计
