人教版八年级下册数学平行四边形的性质 课件(共17张PPT)
文档属性
| 名称 | 人教版八年级下册数学平行四边形的性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 14:55:07 | ||
图片预览


文档简介
(共17张PPT)
第十八章 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角特征
问题1 观察下列图片,它们是否都有平行四边形的形象?
两组对边分别平行的四边形叫做平行四边形.
平行四边形定义:
一、创设情境 导入新课
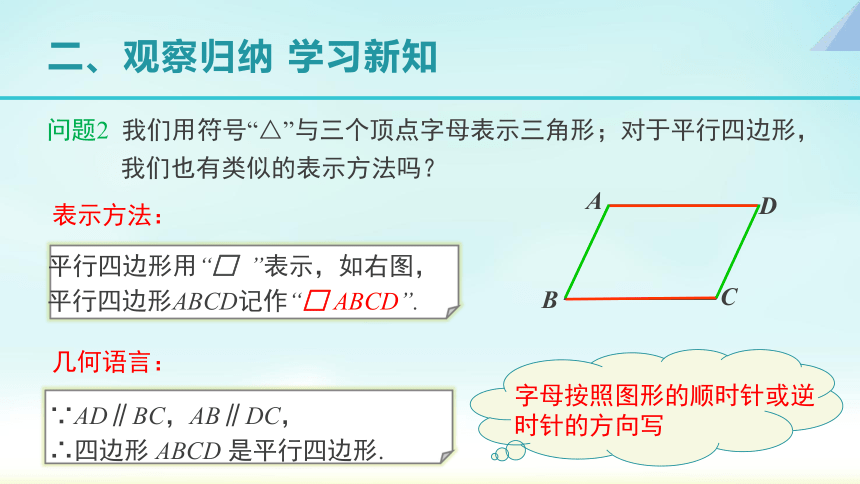
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,
我们也有类似的表示方法吗?
.
∵AD∥BC,AB∥DC,
∴四边形 ABCD 是平行四边形.
字母按照图形的顺时针或逆时针的方向写
.
平行四边形用“□ ”表示,如右图,
平行四边形ABCD记作“□ ABCD”.
表示方法:
几何语言:
A
B
D
C
二、观察归纳 学习新知
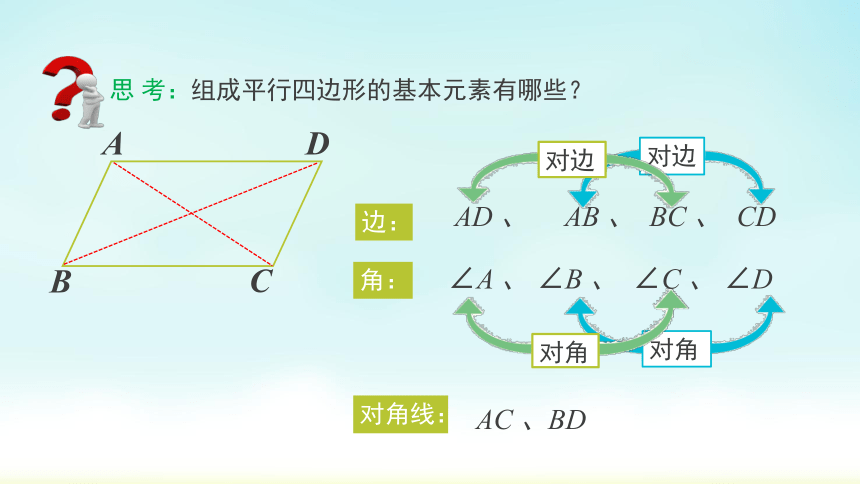
思 考:组成平行四边形的基本元素有哪些?
A
B
D
C
边:
角:
AD 、 AB 、 BC 、 CD
∠A 、 ∠B 、 ∠C 、 ∠D
对边
对边
对角
对角
对角线:
AC 、
BD
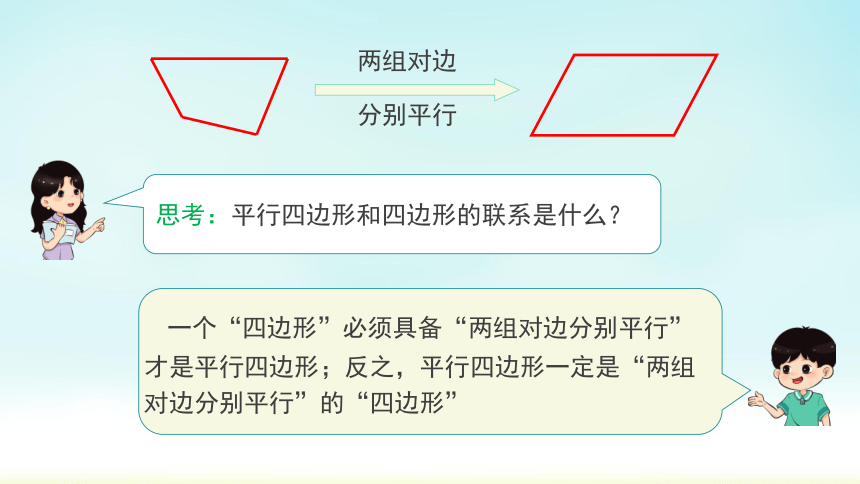
两组对边
分别平行
思考:平行四边形和四边形的联系是什么?
一个“四边形”必须具备“两组对边分别平行”才是平行四边形;反之,平行四边形一定是“两组对边分别平行”的“四边形”
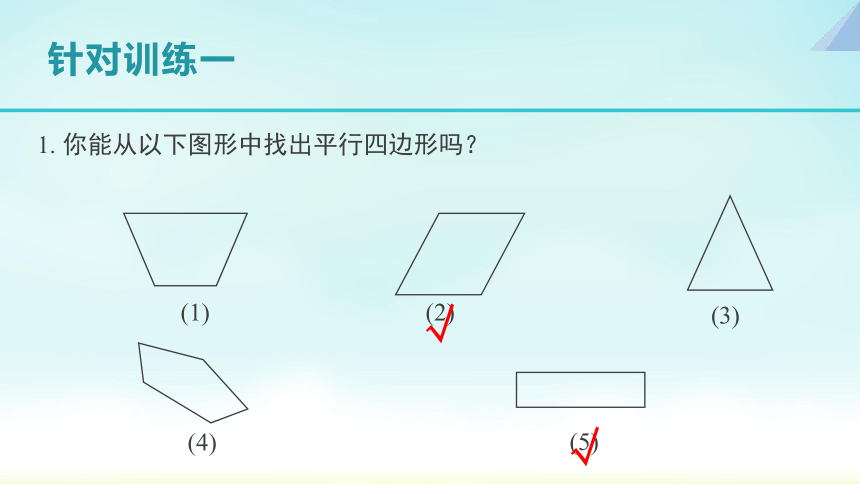
1. 你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
针对训练一
√
√
D
A
B
C
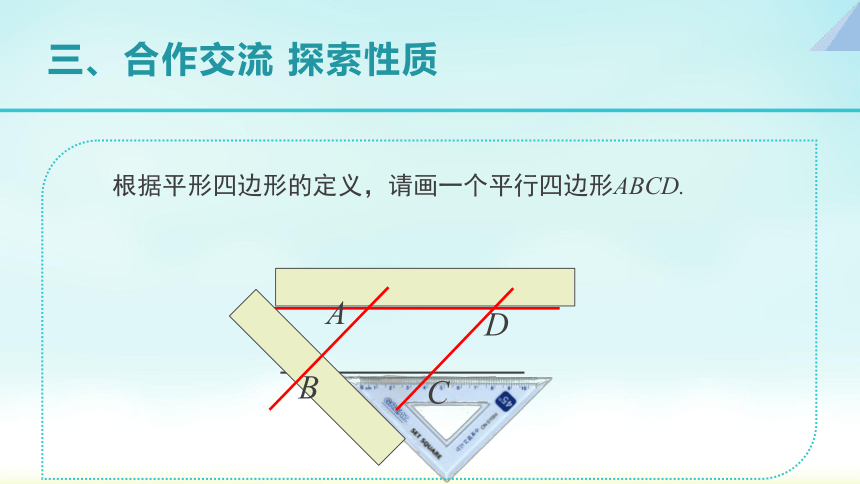
根据平形四边形的定义,请画一个平行四边形ABCD.
三、合作交流 探索性质
.
三、合作交流 探索性质
先独立完成课本P41探究,再以小组为单位合作交流;
1、画一画
3、量一量(误差)
2、猜一猜
猜想:AB=DC,AD=BC
∠A=∠C,∠B=∠D
A
B
C
D
已知:四边形 ABCD 是平行四边形(如图 ).
求证:AD = BC,AB = CD,
∠BAD = ∠BCD,∠B = ∠D.
A
B
C
D
1
3
4
2
证一证
分析:
求证 AD = BC,AB = CD
AD∥BC
AB∥CD
连接 AC
全等
AC 是公共边
AD = BC,AB = CD,
∠B =∠D
△ABC≌△CDA
∠1 =∠2,
∠3 =∠4
平行四边形的对边相等.
几何语言表述:
∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,AD = BC,
∠A =∠C,∠B = ∠D
A
B
C
D
四、归纳总结 巩固提升
平行四边形的对角相等.
平行四边形的性质:
1. 如图,在□ABCD 中.
(1) 若∠A = 130°,则∠B =______ ,∠C =______ , ∠D =______.
(2) 若 AB = 3,BC = 5,则它的周长 = ______.
C
D
A
B
50°
130°
50°
16
针对训练二
平行四边形的对边平行且相等;
平行四边形的对角相等、邻角互补.
(3) 若∠A + ∠C = 200°,则∠A =_____,∠B =______.
100°
80°
证明:∵ 四边形 ABCD 是平行四边形,
∴ ∠A = ∠C,AD = CB.
∵∠AED = ∠CFB = 90°,
∴ △ADE≌△CBF (AAS),
∴ AE = CF.
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE = CF.
D
A
B
C
F
E
思考 在上述证明中还能得出什么结论?
DE = BF
五、学以致用 典例精析
例2 直线a∥b,A,C是直线a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?为什么?
D
C
A
B
性质:两条平行线间的距离处处相等.
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
b
a
两点之间的距离 连接两点之间的线段的长度
点到直线的距离 点到直线垂线段的长度
两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离
B
A
B
A
B
A
P
Q
b
a
1. 已知直线 a∥b,点M到直线 a 的距离是6cm,到直线 b 的距离是3cm,那么直线 a 和直线 b之间的距离为 ____________.
3 cm或 9cm
针对训练三
分析:作出草图;分点M在a, b的同侧, 点M在a, b之间两种情况讨论求解.
.
M
b
a
b
a
.
M
图一
图二
01
02
03
平行四边形的定义
平行四边形的性质
平行四边形的综合运用
六、当堂小结 理顺新知
你今天学到了什么知识?
七、拓展训练 深化理解
拓展题:△ABC是等腰三角形,AB=AC,P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上,求证:PE+PF=AB.
第十八章 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角特征
问题1 观察下列图片,它们是否都有平行四边形的形象?
两组对边分别平行的四边形叫做平行四边形.
平行四边形定义:
一、创设情境 导入新课
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,
我们也有类似的表示方法吗?
.
∵AD∥BC,AB∥DC,
∴四边形 ABCD 是平行四边形.
字母按照图形的顺时针或逆时针的方向写
.
平行四边形用“□ ”表示,如右图,
平行四边形ABCD记作“□ ABCD”.
表示方法:
几何语言:
A
B
D
C
二、观察归纳 学习新知
思 考:组成平行四边形的基本元素有哪些?
A
B
D
C
边:
角:
AD 、 AB 、 BC 、 CD
∠A 、 ∠B 、 ∠C 、 ∠D
对边
对边
对角
对角
对角线:
AC 、
BD
两组对边
分别平行
思考:平行四边形和四边形的联系是什么?
一个“四边形”必须具备“两组对边分别平行”才是平行四边形;反之,平行四边形一定是“两组对边分别平行”的“四边形”
1. 你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
针对训练一
√
√
D
A
B
C
根据平形四边形的定义,请画一个平行四边形ABCD.
三、合作交流 探索性质
.
三、合作交流 探索性质
先独立完成课本P41探究,再以小组为单位合作交流;
1、画一画
3、量一量(误差)
2、猜一猜
猜想:AB=DC,AD=BC
∠A=∠C,∠B=∠D
A
B
C
D
已知:四边形 ABCD 是平行四边形(如图 ).
求证:AD = BC,AB = CD,
∠BAD = ∠BCD,∠B = ∠D.
A
B
C
D
1
3
4
2
证一证
分析:
求证 AD = BC,AB = CD
AD∥BC
AB∥CD
连接 AC
全等
AC 是公共边
AD = BC,AB = CD,
∠B =∠D
△ABC≌△CDA
∠1 =∠2,
∠3 =∠4
平行四边形的对边相等.
几何语言表述:
∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,AD = BC,
∠A =∠C,∠B = ∠D
A
B
C
D
四、归纳总结 巩固提升
平行四边形的对角相等.
平行四边形的性质:
1. 如图,在□ABCD 中.
(1) 若∠A = 130°,则∠B =______ ,∠C =______ , ∠D =______.
(2) 若 AB = 3,BC = 5,则它的周长 = ______.
C
D
A
B
50°
130°
50°
16
针对训练二
平行四边形的对边平行且相等;
平行四边形的对角相等、邻角互补.
(3) 若∠A + ∠C = 200°,则∠A =_____,∠B =______.
100°
80°
证明:∵ 四边形 ABCD 是平行四边形,
∴ ∠A = ∠C,AD = CB.
∵∠AED = ∠CFB = 90°,
∴ △ADE≌△CBF (AAS),
∴ AE = CF.
例1 如图,在 □ABCD 中,DE⊥AB,BF⊥CD,垂足分别为E,F.
求证:AE = CF.
D
A
B
C
F
E
思考 在上述证明中还能得出什么结论?
DE = BF
五、学以致用 典例精析
例2 直线a∥b,A,C是直线a上任意两点,点A到直线b的距离和点C到直线b的距离相等吗?为什么?
D
C
A
B
性质:两条平行线间的距离处处相等.
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
b
a
两点之间的距离 连接两点之间的线段的长度
点到直线的距离 点到直线垂线段的长度
两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离
B
A
B
A
B
A
P
Q
b
a
1. 已知直线 a∥b,点M到直线 a 的距离是6cm,到直线 b 的距离是3cm,那么直线 a 和直线 b之间的距离为 ____________.
3 cm或 9cm
针对训练三
分析:作出草图;分点M在a, b的同侧, 点M在a, b之间两种情况讨论求解.
.
M
b
a
b
a
.
M
图一
图二
01
02
03
平行四边形的定义
平行四边形的性质
平行四边形的综合运用
六、当堂小结 理顺新知
你今天学到了什么知识?
七、拓展训练 深化理解
拓展题:△ABC是等腰三角形,AB=AC,P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上,求证:PE+PF=AB.
