人教版八年级下册数学一次函数与方程、不等式教学设计
文档属性
| 名称 | 人教版八年级下册数学一次函数与方程、不等式教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 126.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 15:07:27 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 一次函数与一元一次方程
教科书 书 名:义务教育教科书 数学 八年级下册 出版社:人民教育出版社 出版日期:2013年6月
教学目标
1. 用函数图像的方法解一元一次方程. 2.加深理解数形结合思想. 3.加深数形结合思想的认识与应用. 4.经过活动,会从不同方面认识事物本质的方法.
教学内容
教学重点: 1.函数观点认识一元一次方程. 2.应用一次函数求解一元一次方程. 教学难点: 用函数观点认识一元一次方程.
教学过程
一.探究发现: 1.解下列方程: (1)2x+1=0 (2)2 x +2=0 2.求下列函数与x轴的交点坐标: (1)y=2 x -4 (2)y=2 x +2提问: 它们从形式上看,有什么不同? 二.新课探究: 看下面两个问题之间的关系: 问题: (1)解方程2 x +1=0 (2)一次函数y=2x+1的函数值为0时,求自变量x的值? 从问题的本质上看,(1)和(2)有什么关系? (从“数”的角度看) 解方程2x+1=0 一次函数y=2x+1的函数值为0时,求自量x的值 下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗? (1)2x+1=3; (2)2x+1=0; (3)2x+1=-1. 引导学生从“数”的角度看 一元一次方程问题一次函数问题解方程2x+1=3一次函数y=2x+1的函数值为3时,求自变量x的值解方程2x+1=0一次函数y=2x+1的函数值为0时,求自变量x的值解方程2x+1=-1一次函数y=2x+1的函数值为-1时,求自变量x的值解方程ax+b=0(a一次函数y=ax+b的函数值为0时,求自变量的值
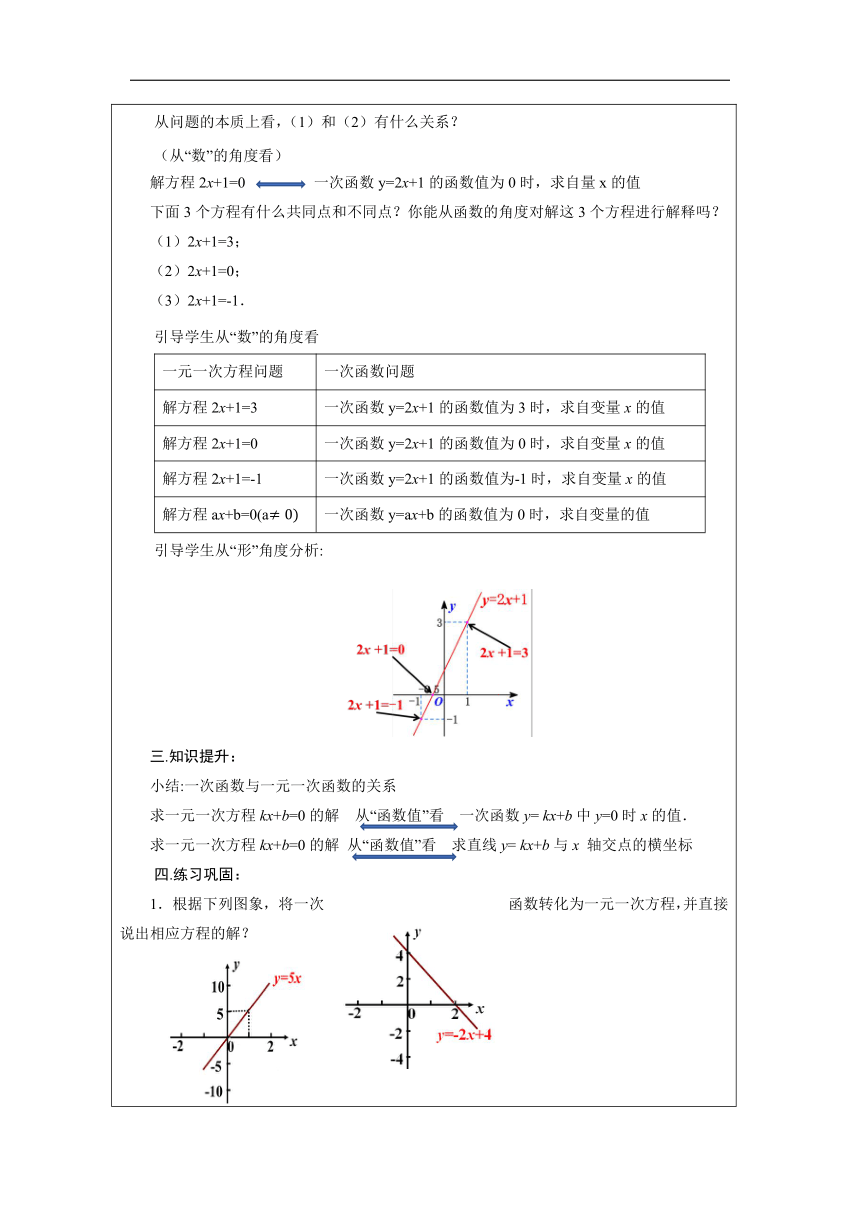
引导学生从“形”角度分析: 三.知识提升: 小结:一次函数与一元一次函数的关系 求一元一次方程kx+b=0的解 从“函数值”看 一次函数y= kx+b中y=0时x的值. 求一元一次方程kx+b=0的解 从“函数值”看 求直线y= kx+b与x 轴交点的横坐标 四.练习巩固: 1.根据下列图象,将一次函数转化为一元一次方程,并直接说出相应方程的解? 2.当x为何值时,y=ax+b的函数值为0? 例 直线y=3x+6与x轴的交点横坐标x的值是方程2x+a=0的解,求a的值。分析:根据直线y=3x+6与x轴相交,可以得到方程3x+6=0,即可解出横坐标x的值为-2,再根据x的值是方程2x+a=0的解,得到-4+a=0,所以求出的a的值为4. 练习: 一次函数y=2x+8与x轴的交点坐标为 ,那么方程2x+8=0的解为 . 4.已知关于x的方程ax+b=0(a的解为x=3,那么直线y=ax+b(a与x轴的交点坐标为 .5.如图,直线y=ax+b,那么方程ax+b=0的解是 . 知识拓展: 一个物体现在的速度为5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?你有哪些方法呢? 解法1:设再过x 秒它的速度为17米/秒, 依题意得,2x +5=17 解得 x =6 答:再过6秒它的速度为17米/秒. 解法2:设速度为y米/秒,时间为x秒, 依题意得: y=2x+5 则当y=17时,2x+5=17,得 2x-12=0,令y=2x-12 由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6. 即再过6秒它的速度为17米/秒. 五.课堂小结: 1.知识:一次函数与一元一次方程的关系 2.方法:类比 数形结合 特殊到一般 六.课后作业:
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
课程基本信息
学科 数学 年级 八年级 学期 春季
课题 一次函数与一元一次方程
教科书 书 名:义务教育教科书 数学 八年级下册 出版社:人民教育出版社 出版日期:2013年6月
教学目标
1. 用函数图像的方法解一元一次方程. 2.加深理解数形结合思想. 3.加深数形结合思想的认识与应用. 4.经过活动,会从不同方面认识事物本质的方法.
教学内容
教学重点: 1.函数观点认识一元一次方程. 2.应用一次函数求解一元一次方程. 教学难点: 用函数观点认识一元一次方程.
教学过程
一.探究发现: 1.解下列方程: (1)2x+1=0 (2)2 x +2=0 2.求下列函数与x轴的交点坐标: (1)y=2 x -4 (2)y=2 x +2提问: 它们从形式上看,有什么不同? 二.新课探究: 看下面两个问题之间的关系: 问题: (1)解方程2 x +1=0 (2)一次函数y=2x+1的函数值为0时,求自变量x的值? 从问题的本质上看,(1)和(2)有什么关系? (从“数”的角度看) 解方程2x+1=0 一次函数y=2x+1的函数值为0时,求自量x的值 下面3个方程有什么共同点和不同点?你能从函数的角度对解这3个方程进行解释吗? (1)2x+1=3; (2)2x+1=0; (3)2x+1=-1. 引导学生从“数”的角度看 一元一次方程问题一次函数问题解方程2x+1=3一次函数y=2x+1的函数值为3时,求自变量x的值解方程2x+1=0一次函数y=2x+1的函数值为0时,求自变量x的值解方程2x+1=-1一次函数y=2x+1的函数值为-1时,求自变量x的值解方程ax+b=0(a一次函数y=ax+b的函数值为0时,求自变量的值
引导学生从“形”角度分析: 三.知识提升: 小结:一次函数与一元一次函数的关系 求一元一次方程kx+b=0的解 从“函数值”看 一次函数y= kx+b中y=0时x的值. 求一元一次方程kx+b=0的解 从“函数值”看 求直线y= kx+b与x 轴交点的横坐标 四.练习巩固: 1.根据下列图象,将一次函数转化为一元一次方程,并直接说出相应方程的解? 2.当x为何值时,y=ax+b的函数值为0? 例 直线y=3x+6与x轴的交点横坐标x的值是方程2x+a=0的解,求a的值。分析:根据直线y=3x+6与x轴相交,可以得到方程3x+6=0,即可解出横坐标x的值为-2,再根据x的值是方程2x+a=0的解,得到-4+a=0,所以求出的a的值为4. 练习: 一次函数y=2x+8与x轴的交点坐标为 ,那么方程2x+8=0的解为 . 4.已知关于x的方程ax+b=0(a的解为x=3,那么直线y=ax+b(a与x轴的交点坐标为 .5.如图,直线y=ax+b,那么方程ax+b=0的解是 . 知识拓展: 一个物体现在的速度为5米/秒,其速度每秒增加2米/秒,再过几秒它的速度为17米/秒?你有哪些方法呢? 解法1:设再过x 秒它的速度为17米/秒, 依题意得,2x +5=17 解得 x =6 答:再过6秒它的速度为17米/秒. 解法2:设速度为y米/秒,时间为x秒, 依题意得: y=2x+5 则当y=17时,2x+5=17,得 2x-12=0,令y=2x-12 由右图看出直线y=2x-12与x轴的交点为(6,0),得x=6. 即再过6秒它的速度为17米/秒. 五.课堂小结: 1.知识:一次函数与一元一次方程的关系 2.方法:类比 数形结合 特殊到一般 六.课后作业:
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
