图形的初步认识单元测试卷[上学期]

2005年秋七年级数学单元测试卷
（图形的初步认识）
班级_______ 姓名___________ 座号______ 成绩_________
1、 填空题：（每小题３分，共39分）
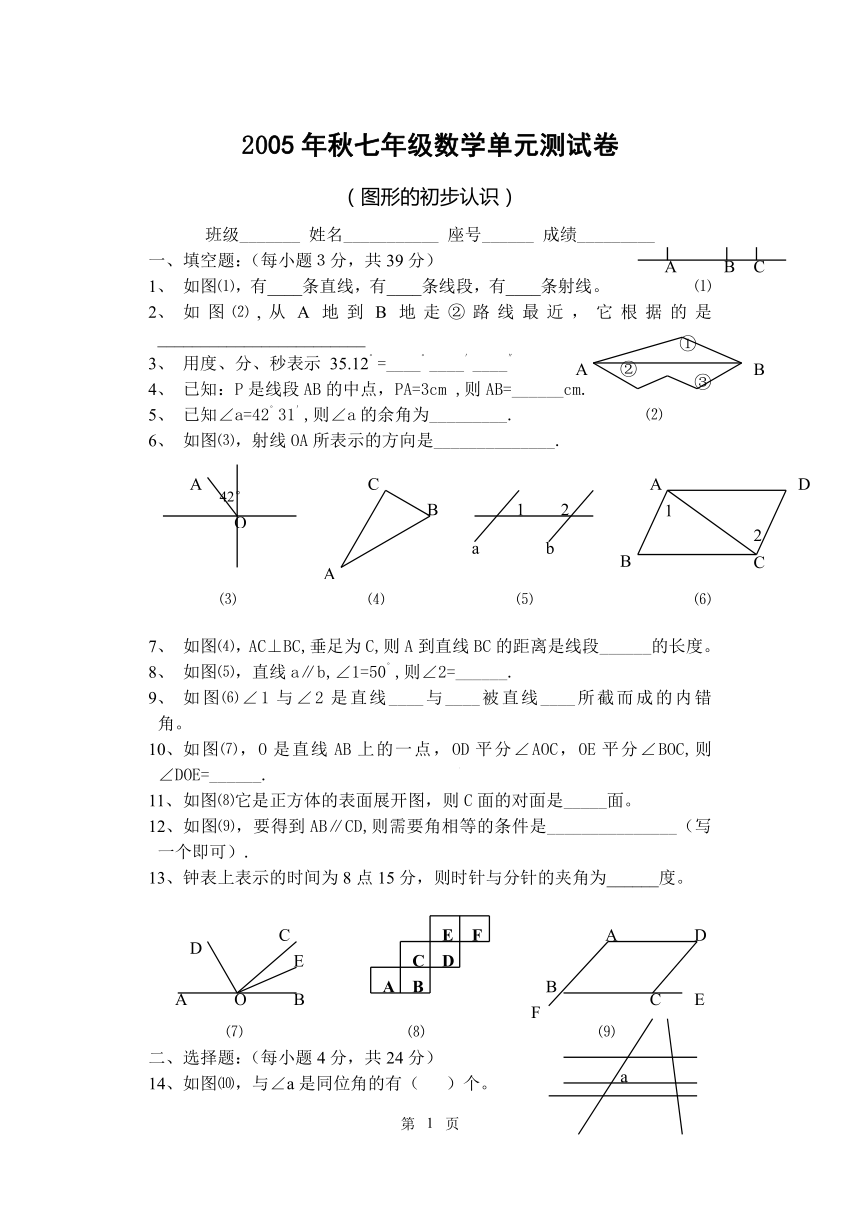
1、 如图⑴，有____条直线，有____条线段，有____条射线。 ⑴
2、 如图⑵,从A地到B地走②路线最近，它根据的是________________________
3、 用度、分、秒表示 35.12°=____°____′____″
4、 已知：P是线段AB的中点，PA=3cm ,则AB=______cm.
5、 已知∠a=42°31′,则∠a的余角为_________. ⑵
6、 如图⑶，射线OA所表示的方向是______________.
7、 如图⑷，AC⊥BC,垂足为C,则A到直线BC的距离是线段______的长度。
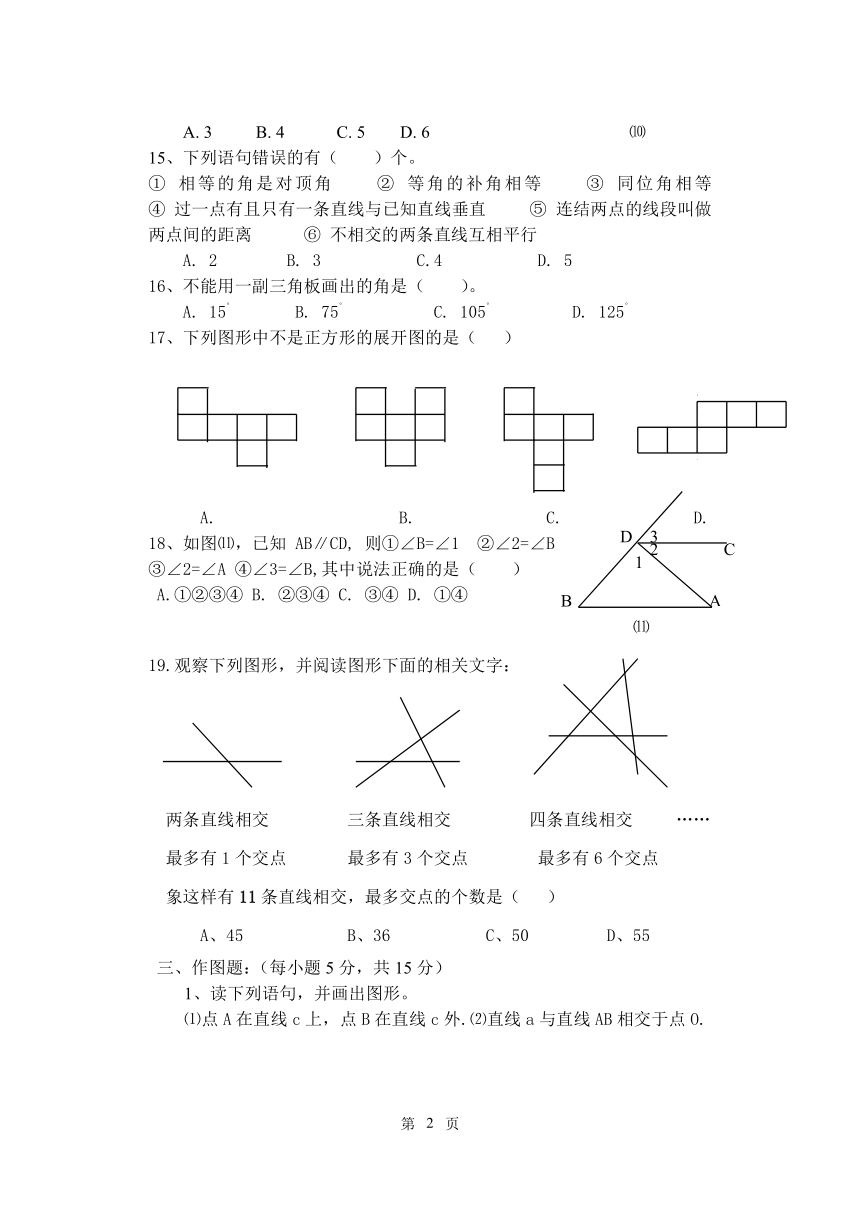
8、 如图⑸，直线a∥b,∠1=50°,则∠2=______.
9、 如图⑹∠1与∠2是直线____与____被直线____所截而成的内错 角。
10、 如图⑺，O是直线AB上的一点，OD平分∠AOC，OE平分∠BOC,则 ∠DOE=______.
11、 如图⑻它是正方体的表面展开图，则C面的对面是_____面。
12、 如图⑼，要得到AB∥CD,则需要角相等的条件是_______________（写一个即可）.
13、 钟表上表示的时间为8点15分，则时针与分针的夹角为______度。
⑺ ⑻ ⑼
2、 选择题：（每小题4分，共24分）
14、如图⑽，与∠a是同位角的有（ ）个。
A. 3 B. 4 C. 5 D. 6 ⑽
15、下列语句错误的有（ ）个。
① 相等的角是对顶角 ② 等角的补角相等 ③ 同位角相等 ④ 过一点有且只有一条直线与已知直线垂直 ⑤ 连结两点的线段叫做两点间的距离 ⑥ 不相交的两条直线互相平行
A. 2 B. 3 C.4 D. 5
16、不能用一副三角板画出的角是（　　）。
A. 15° B. 75° C. 105° D. 125°
17、下列图形中不是正方形的展开图的是（ ）
A. B. C. D.
18、如图⑾，已知 AB∥CD, 则①∠B=∠1 ②∠2=∠B
③∠2=∠A ④∠3=∠B,其中说法正确的是（ ）
A.①②③④ B. ②③④ C. ③④ D. ①④
⑾
19.观察下列图形，并阅读图形下面的相关文字：
两条直线相交 三条直线相交 四条直线相交 ……
最多有1个交点 最多有3个交点 最多有6个交点
象这样有11条直线相交，最多交点的个数是（ ）
A、45 B、36 C、50 D、55
三、作图题：（每小题5分，共15分）
1、读下列语句，并画出图形。
⑴点A在直线c上，点B在直线c外.⑵直线a与直线AB相交于点O.
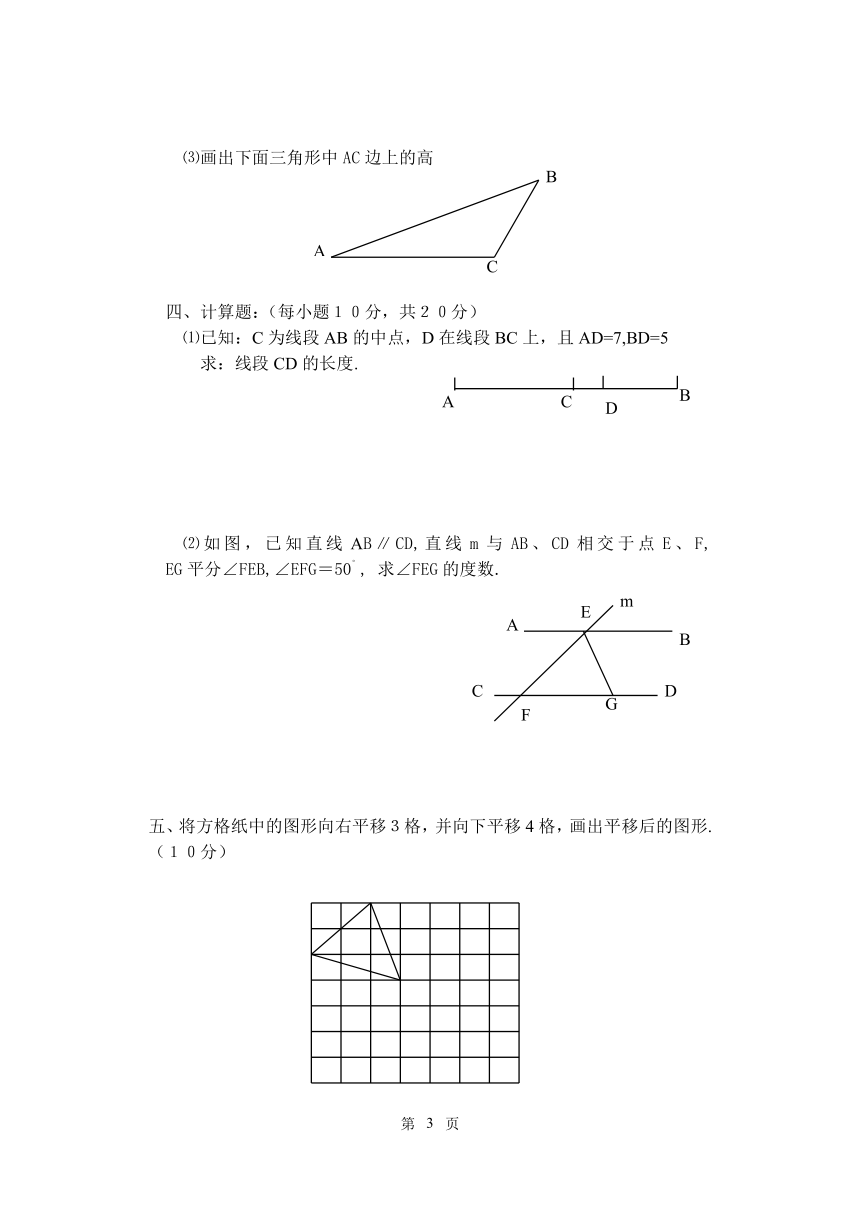
⑶画出下面三角形中AC边上的高
　四、计算题：（每小题１０分，共２０分）
⑴已知：C为线段AB的中点，D在线段BC上，且AD=7,BD=5
求：线段CD的长度.
⑵如图，已知直线AB∥CD,直线m与AB、CD相交于点E、F, EG平分∠FEB,∠EFG＝50°, 求∠FEG的度数.
五、将方格纸中的图形向右平移３格，并向下平移4格，画出平移后的图形.（１０分）
六、填空或填写理由：（每空２分，共２２分）
　⑴　∵∠１＋∠２＝90°,∠１＋∠３＝90°（已知）
∴∠２＝∠３（　　　　　　　　　　　　　）
⑵ ∵a∥b, a∥c （已知）
∴b∥c( )
⑶如图① ∵∠（　　）＝∠（　　）（已知）
　　　　 ∴AB∥CD（　　　　　　　　　　　 ）
　⑷如图②，直线a∥b,∠３＝85°,求∠１，∠２的度数. ①
解：　 ∵a∥b（　　　）
　　　　∴∠１＝∠４（ ）
∵∠4＝∠３（ ），∠３=85°（ ）
∴∠１=（ ）（等量代换）
又∵∠2＋∠3＝85°，
∴∠2=（ ）（等式的性质）
②
七、下列物体是由四个小正方形搭成的，请画出它的正视图，左视图和俯视图。（10分）
八、如下图，∠１＝∠C, ∠2与∠3互补，那么AB与 EF平行吗？为什么？（10分）
参考答案：
一、1、1 ，3 ，6 2、两点之间，线段最短 3、35，7，12 4、6
5、47°29′ 6、北偏西38° 7、AC 8、130° 9、AB CD AC 10、90°
11、 F 12、∠DCE=∠ABC或∠FBC=∠BCD 13、157．5
二、
A C D B C D
三、
1、 2、
3、
四、
(1)解∵AD=7,BD=5 (2)解：∵AB∥CD(已知)
∴AB=AD+BD=12 ∴∠EFG+∠FEB=180°(两直线平行，同旁内角互补)
∵C是AB的中点 ∵∠EFG=50°(已知)
∴AC=AB=6 ∴∠FEB=130° （等式的性质）
∴CD=AD-AC=7-6=1 ∵EG平分∠FEB (已知)
∴∠FEG=∠FEB=65°(角平分线的定义)
五、
六、
（1）同角的余角相等
（2）如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
（3）3； 4； 内错角相等，两直线平行。
（4）已知；两直线平行，同位角相等；对顶角相等；已知；85° ；95°
七、解：
正视图为： 左视图为： 俯视图为：
八、
解：∵∠1=∠C(已知)
∴DE∥BC（同位角相等，两直线平行）
∴∠3与∠B互补 （两直线平行，同旁内角互补）
∵∠2与∠3互补(已知)
∴∠2=∠B （同角的补角相等）
∴AB∥EF（同位角相等，两直线平行）
注：本题解法不唯一。
AA
a
B
C
A
B
C
D
F
E
a
b
A
B
C
D
A
B
O
A
A
B
C
a
b
A
B
C
D
⑶
⑷
⑸
⑹
B
B
A
D
m
C
D
G
E
F
B
D
C
A
E
O
F
A
D
B
C
D
B
E
C
A
E
F
C
A
D
A
B
C
A
B
C
①
②
③
4
2
3
1
2
1
3
a
42°
2
2
1
1
4
3
3
2
1
2
1
A
B
O
c
A
B．． ....
．
A
B
C
PAGE
1
第 页