6.2.3向量的数乘运算 课件(共23张PPT)
文档属性
| 名称 | 6.2.3向量的数乘运算 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 04:49:07 | ||
图片预览



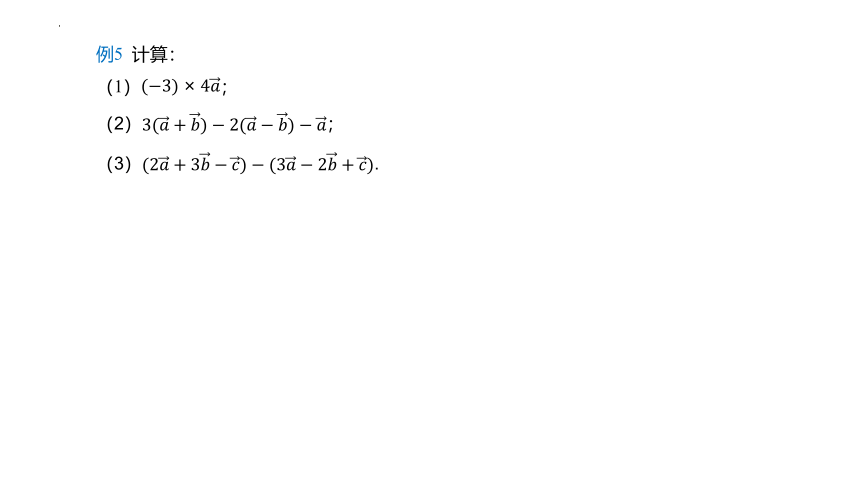


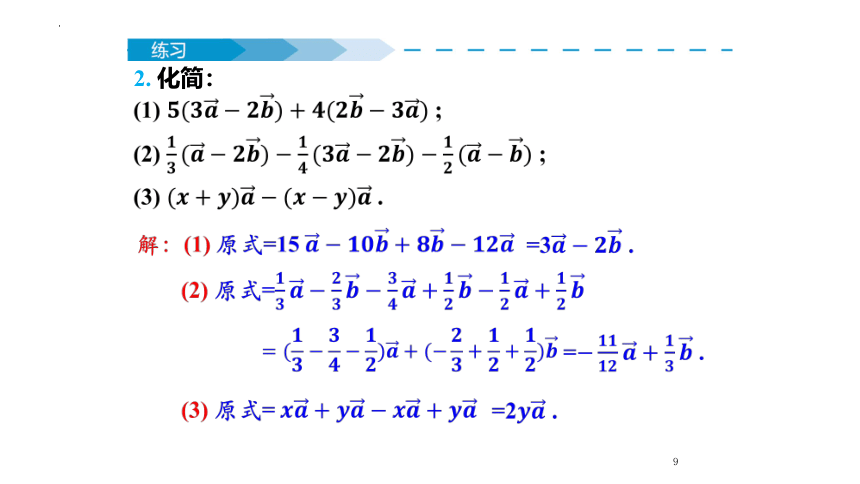
文档简介
(共23张PPT)
§6.2.3 向量的数乘运算
6.2 平面向量的运算
温故知新
1.向量的加法运算:
①三角形法则:
②平行四边形法则:
2.向量的减法运算:
首尾相接,首指向尾
起点相同,对角为和
思考:向量有乘法运算吗?怎么定义呢?运算结果是什么量呢?
共起点,连终点,指被减
问题引入
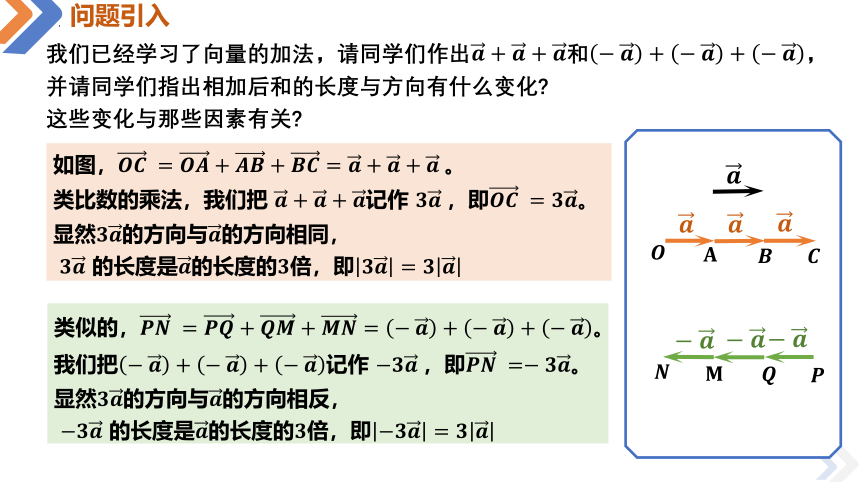
我们已经学习了向量的加法,请同学们作出和,
并请同学们指出相加后和的长度与方向有什么变化
这些变化与那些因素有关
如图,。
类比数的乘法,我们把 记作 ,即。
显然的方向与的方向相同,
的长度是的长度的倍,即
类似的,。
我们把记作 ,即。
显然的方向与的方向相反,
的长度是的长度的倍,即
生成新知
一般地,我们规定实数与向量的积是一个向量, 这种运算叫做向量的数乘,记作。
定义
长度:
方向:当时,的方向与的方向相同;
当时, 的方向与的方向相反;
当时,
规定
注意
1.向量数乘的结果仍然是向量;
2.实数和向量可以相乘,但不能相加减, , 无意义;
向量数乘的几何意义是什么
再探新知
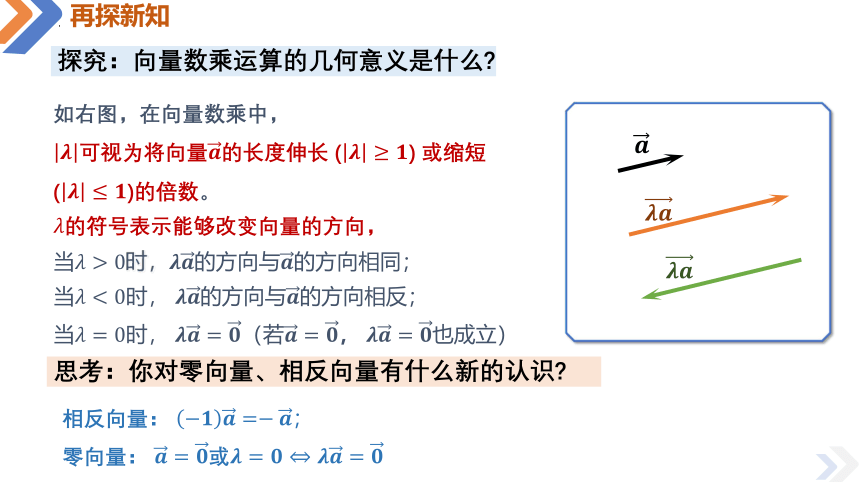
探究:向量数乘运算的几何意义是什么
如右图,在向量数乘中,
可视为将向量的长度伸长 () 或缩短 ()的倍数。
的符号表示能够改变向量的方向,
当时,的方向与的方向相同;
当时, 的方向与的方向相反;
当时, (若, 也成立)
思考:你对零向量、相反向量有什么新的认识
相反向量: ;
零向量: 或
例5 计算:
(1);
(2);
(3).
例5 计算:
(1);
(2);
(3).
解:(1)原式;
(2)原式 ;
(3)原式 .
应用新知
例1.把下列小题中的向量表示为向量的数乘形式。
9
作者:湛江市第五中学钟景荣
2. 化简:
知识讲解
(1)向量得数乘运算类似于多项式的代数运算,实数运算中的去括号、移项、合并同类项、提取公因式等变形手段在数与向量的乘积中同样适用,但是这里的“同类项”“公因式”指向量,实数看作是向量的系数.
(2)向量也可以通过列方程来解—把所求向量当作未知数,利用解代方程的方法求解.在运算过程中要多注意观察,恰当运用运算律,简化运算.
总结
反过来,
反过来,
向量共线定理:
向量( ≠ )共线的充要条件是:存在唯一一个实数,使
14
作者:湛江市第五中学钟景荣
向量共线定理:
(2)当时, 若, 则对任意实数λ, 都有=λ, 这与有唯一一个实数λ相矛盾.
与共线
向量与共线充要条件是:
(1)当=时, 若≠ , 则不存在实数λ, 使=λ, 但此时与共线;
当λ>0时,与同向共线;当λ<0时,与反向共线.
存在唯一一个实数λ,使得=λ.
向量共线定理中为什么规定
若与不共线,且λ=, 则必有λ==0.
15
1. 判断下列各小题中的向量与是否共线:
解:(1)因为,
作者:湛江市第五中学钟景荣
所以与共线.
(1) , ;
(2) , .
(2)因为,
所以与共线.
与共线
A
B
C
D
E
例7.如图,已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
A
B
C
O
18
过A作直线AC,
解:分别作, , ,
=+2-(+)=,
事实上, 因为
所以=2 ,
观察图6.2-17(1)(2)发现, 不论向量, 怎样变化, 点B始终在直线AC上, 猜想A, B, C三点共线.
=
=+3-(+)=2,
=
因此A, B, C三点共线.
向量共线定理主要用来证明两条直线平行, 三点共线等问题.
例7.如图,已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
A
B
O
C
且有公共点A
已知两个非零向量
不共线,如果
20
与不在同一直线上
直线AB∥直线CD
2. 证明 三点共线: =λ
向量共线定理
与共线
向量与共线充要条件是:
存在唯一一个实数λ,
当λ>0时,与共线同向;当λ<0时,与共线反向.
定理的应用:
1. 证明 向量共线
3. 证明 两直线平行:
=λ //
使得=λ.
A, B, C三点共线
21
例8 已知, 是两个不共线的向量, 向量, 共线, 求实数t的值.
解:由, 不共线, 易知向量为非零向量.
由向量, 共线,
否则, 不妨设, 则= ,由两个向量共线的充要条件知, 共线, 这与已知条件相矛盾.
可知存在实数λ, 使得
=
即=.
由于, 不共线, 必有==0 .
对于两个非零向量, 只有共线, 它们的和或差才有可能为零向量.
因此, 当向量, 共线时, .
22
由
解得 .
解:由, 不共线, 易知向量为非零向量.
由向量, 共线,
否则, 不妨设, 则= ,由两个向量共线的充要条件知, 共线, 这与已知条件相矛盾.
可知存在实数λ, 使得
=
即=.
由于, 不共线, 必有==0 .
对于两个非零向量, 只有共线, 它们的和或差才有可能为零向量.
23
作者:湛江市第五中学钟景荣
∵与是共线向量,
∴存在λ∈R,使得.
∴
所以实数k的值是-4.
解得
即2+k=λ(-2),
∴ 2+k=λ-2λ ,
3. 已知, 是两个不共线的向量, =-2, =2+k,
若与是共线向量, 求实数k的值.
解:由已知得,
即.
∴
解得k=-4.
所以实数k的值是-4.
§6.2.3 向量的数乘运算
6.2 平面向量的运算
温故知新
1.向量的加法运算:
①三角形法则:
②平行四边形法则:
2.向量的减法运算:
首尾相接,首指向尾
起点相同,对角为和
思考:向量有乘法运算吗?怎么定义呢?运算结果是什么量呢?
共起点,连终点,指被减
问题引入
我们已经学习了向量的加法,请同学们作出和,
并请同学们指出相加后和的长度与方向有什么变化
这些变化与那些因素有关
如图,。
类比数的乘法,我们把 记作 ,即。
显然的方向与的方向相同,
的长度是的长度的倍,即
类似的,。
我们把记作 ,即。
显然的方向与的方向相反,
的长度是的长度的倍,即
生成新知
一般地,我们规定实数与向量的积是一个向量, 这种运算叫做向量的数乘,记作。
定义
长度:
方向:当时,的方向与的方向相同;
当时, 的方向与的方向相反;
当时,
规定
注意
1.向量数乘的结果仍然是向量;
2.实数和向量可以相乘,但不能相加减, , 无意义;
向量数乘的几何意义是什么
再探新知
探究:向量数乘运算的几何意义是什么
如右图,在向量数乘中,
可视为将向量的长度伸长 () 或缩短 ()的倍数。
的符号表示能够改变向量的方向,
当时,的方向与的方向相同;
当时, 的方向与的方向相反;
当时, (若, 也成立)
思考:你对零向量、相反向量有什么新的认识
相反向量: ;
零向量: 或
例5 计算:
(1);
(2);
(3).
例5 计算:
(1);
(2);
(3).
解:(1)原式;
(2)原式 ;
(3)原式 .
应用新知
例1.把下列小题中的向量表示为向量的数乘形式。
9
作者:湛江市第五中学钟景荣
2. 化简:
知识讲解
(1)向量得数乘运算类似于多项式的代数运算,实数运算中的去括号、移项、合并同类项、提取公因式等变形手段在数与向量的乘积中同样适用,但是这里的“同类项”“公因式”指向量,实数看作是向量的系数.
(2)向量也可以通过列方程来解—把所求向量当作未知数,利用解代方程的方法求解.在运算过程中要多注意观察,恰当运用运算律,简化运算.
总结
反过来,
反过来,
向量共线定理:
向量( ≠ )共线的充要条件是:存在唯一一个实数,使
14
作者:湛江市第五中学钟景荣
向量共线定理:
(2)当时, 若, 则对任意实数λ, 都有=λ, 这与有唯一一个实数λ相矛盾.
与共线
向量与共线充要条件是:
(1)当=时, 若≠ , 则不存在实数λ, 使=λ, 但此时与共线;
当λ>0时,与同向共线;当λ<0时,与反向共线.
存在唯一一个实数λ,使得=λ.
向量共线定理中为什么规定
若与不共线,且λ=, 则必有λ==0.
15
1. 判断下列各小题中的向量与是否共线:
解:(1)因为,
作者:湛江市第五中学钟景荣
所以与共线.
(1) , ;
(2) , .
(2)因为,
所以与共线.
与共线
A
B
C
D
E
例7.如图,已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
A
B
C
O
18
过A作直线AC,
解:分别作, , ,
=+2-(+)=,
事实上, 因为
所以=2 ,
观察图6.2-17(1)(2)发现, 不论向量, 怎样变化, 点B始终在直线AC上, 猜想A, B, C三点共线.
=
=+3-(+)=2,
=
因此A, B, C三点共线.
向量共线定理主要用来证明两条直线平行, 三点共线等问题.
例7.如图,已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
A
B
O
C
且有公共点A
已知两个非零向量
不共线,如果
20
与不在同一直线上
直线AB∥直线CD
2. 证明 三点共线: =λ
向量共线定理
与共线
向量与共线充要条件是:
存在唯一一个实数λ,
当λ>0时,与共线同向;当λ<0时,与共线反向.
定理的应用:
1. 证明 向量共线
3. 证明 两直线平行:
=λ //
使得=λ.
A, B, C三点共线
21
例8 已知, 是两个不共线的向量, 向量, 共线, 求实数t的值.
解:由, 不共线, 易知向量为非零向量.
由向量, 共线,
否则, 不妨设, 则= ,由两个向量共线的充要条件知, 共线, 这与已知条件相矛盾.
可知存在实数λ, 使得
=
即=.
由于, 不共线, 必有==0 .
对于两个非零向量, 只有共线, 它们的和或差才有可能为零向量.
因此, 当向量, 共线时, .
22
由
解得 .
解:由, 不共线, 易知向量为非零向量.
由向量, 共线,
否则, 不妨设, 则= ,由两个向量共线的充要条件知, 共线, 这与已知条件相矛盾.
可知存在实数λ, 使得
=
即=.
由于, 不共线, 必有==0 .
对于两个非零向量, 只有共线, 它们的和或差才有可能为零向量.
23
作者:湛江市第五中学钟景荣
∵与是共线向量,
∴存在λ∈R,使得.
∴
所以实数k的值是-4.
解得
即2+k=λ(-2),
∴ 2+k=λ-2λ ,
3. 已知, 是两个不共线的向量, =-2, =2+k,
若与是共线向量, 求实数k的值.
解:由已知得,
即.
∴
解得k=-4.
所以实数k的值是-4.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
