5.2 旋转 导学课件(共32张PPT) 2022—2023学年湘教版数学七年级下册
文档属性
| 名称 | 5.2 旋转 导学课件(共32张PPT) 2022—2023学年湘教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 924.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 16:30:44 | ||
图片预览










文档简介
(共32张PPT)
5.2 旋转
第五章 轴对称与旋转
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
旋转的相关概念
旋转的性质
旋转作图
感悟新知
知识点
旋转的相关概念
1
1.图形旋转的概念:
将一个平面图形上的每一个点,绕这个平面内一定点旋转同一个角α (即把图形上每一个点与定点的连线绕定点旋转角α ) ,得到新图形,图形的这种变换叫做旋转 .
此处旋转是指平面内的变换,因此,“平
面内”这一条件不可忽略 .
感悟新知
特别提醒
1. 旋转中心可以是图形外的一点,也可以是图形上的一点,还可以是图形内的一点 .
2. 旋转方向可以是顺时针方向,也可以是逆
时针方向 .
3. 某些特殊图形经过旋转变换后得到的新图形可以与原图形重合,如圆绕圆心旋转任意角度还是原位置的圆 .
感悟新知
2.图形旋转的三要素:
旋转中心 旋转过程中的定点,即不动的点,如右图中的定点 O
旋转角 转动的角(在本书中,旋转角不大于360°),如右图中的∠ POP′ 旋转方向 顺时针或逆时针,如右图中时针的旋转方向为顺时针 感悟新知
3. 图形旋转中的对应元素(如图 5.2 - 1 )
感悟新知
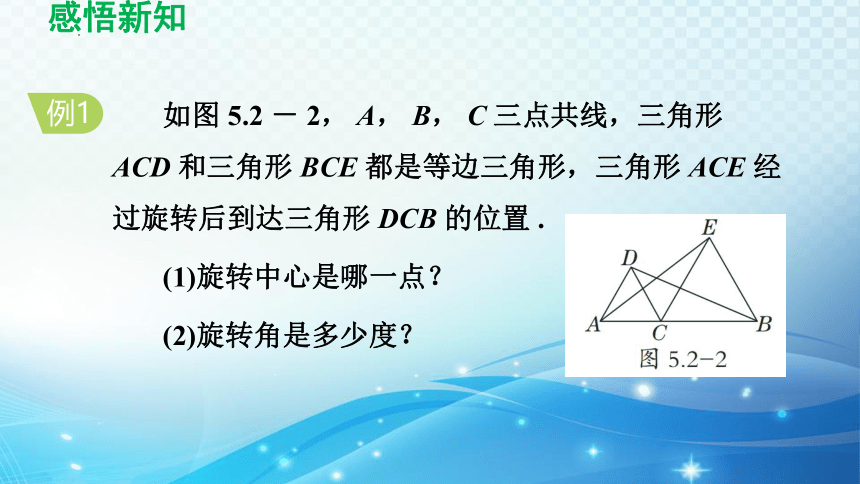
如图 5.2 - 2, A, B, C 三点共线,三角形 ACD 和三角形 BCE 都是等边三角形,三角形 ACE 经过旋转后到达三角形 DCB 的位置 .
(1)旋转中心是哪一点?
(2)旋转角是多少度?
例1
感悟新知
解题秘方:紧扣“图形旋转时,固定不动的点是旋转中心,转动的角是旋转角”进行判断 .
感悟新知
解: (1)点 C 是在三角形 ACE 旋转过程中不动的点,
所以点 C 是旋转中心 .
(2)三角形 ACE 旋转后到达三角形 DCB 的位置, AC 绕点 C 旋转到 DC, AC 转过的角即∠ ACD 就是旋转角 .
因为三角形 ACD 是等边三角形,
所以∠ ACD=60°,即旋转角是 60° .
感悟新知
解法提醒
三角形 ACE 经过旋转后得到三角形DCB.
(1)三角形在旋转过程中不动的点是旋转中心;
(2)两个三角形的对应边所夹的角即为旋转角.
感悟新知
知识点
测量质量
2
一个图形和它经过旋转所得到的图形中,具有如下性质:
(1)对应点到旋转中心的距离相等 .
(2)两组对应点分别与旋转中心的连线所成的角相等 .
(3)旋转不改变图形的形状和大小 .
感悟新知
如图 5.2 - 3, 将三角形 ABC 绕点 O 逆时针旋转 60°得到三角形 A′ B′ C′,则三角形 ABC 能与三角形 A′ B′ C′完全重合 . 对应线段 AB=A′ B′, BC=B′ C′, CA=C′ A′;对应角∠ A= ∠ A′,∠ B= ∠ B′,∠ C= ∠ C′ .
感悟新知
在图 5.2 - 3 中, 对 应 点 A, A ′与 点 O 的 距 离 相 等, 即AO=A ′ O. 类 似 地, BO=B ′ O, CO=C ′ O, 对 应 点 A, A ′与 B, B′与旋转中心的连线所成的角相等,且等于旋转角,即∠ AOA′ = ∠ BOB′ =60° .
感悟新知
特别提醒
1. 要注意区分旋转角与对应角、对应点到旋转中心的距离与对应线段的长度 . 旋转角是指图形旋转过的角度,而非图形中的角度,对应角是指图形旋转前、后能够互相重合的角,是图形中的角;对应点到旋转中心的距离是图形上的点到旋转中心的距离,对应线段的长度则是图形的边长 .
感悟新知
2. 在旋转形成的图形中,找相等的线段一般包含两类:
①旋转前后图形中的对应线段;②各对应点到旋转中心的距离 .
找相等的角也包含两类:
①旋转前后图形中的对应角;②各对应点与旋转中心的连线的夹角 .
感悟新知
如图5.2 - 4, 在正方形 ABCD 中,点 E 在 BC 上,∠ FDE=45°,三角形 DEC 按顺时针方向旋转一个角度后到达三角形 DGA 的位置 .
例2
感悟新知
解题秘方:紧扣旋转的性质解答相关问题 .
感悟新知
(1)图中哪一个点是旋转中心?旋转角是多少度?
解:图中的点 D 是旋转中心,旋转角是 90° .
感悟新知
(2)请写出图中旋转图形的对应线段与对应角 .
解:图中 DE 与 DG, DC 与 DA, EC与 GA 是对应线段;
∠ CDE 与 ∠ ADG, ∠ C 与 ∠ DAG,
∠ DEC 与∠ G 是对应角 .
感悟新知
(3)请写出图中除正方形的四条边、直角外的相等线段与相等角及能够完全重合的三角形 .
解:相等线段: DG=DE, GA=EC;
相 等 角: ∠ G= ∠ DEC= ∠ ADE, ∠ ADG= ∠ CDE,
∠ GDF= ∠ FDE,∠ AFD= ∠ CDF;
能够完全重合的三角形:三角形 DEC 与三角形 DGA.
感悟新知
(4)求∠ GDF 的度数 .
解:因为三角形 DEC 绕点 D 顺时针旋转 90°到三角形DGA 的位置,
所以∠ GDE=90° .
所以∠ GDF= ∠ GDE - ∠ FDE=90° - 45° =45° .
感悟新知
解题通法
由于旋转前后两个图形的形状、大小未发生改变,所以我们在利用旋转来解决与其相关的问题时应抓住以下三点:
1. 明确旋转中的“变” 与“不变”;
2. 找准旋转前后的“对应关系”,正确判断旋转前后图形的对应点、对应角、对应线段以及旋转角,这是理解和应用旋转特征的基础;
3. 充分挖掘旋转过程中的相等关系.
感悟新知
知识点
旋转作图
3
1. 作图依据:
旋转的性质,即对应点到旋转中心的距离相等,每组对应点都旋转相同的角度 .
感悟新知
2. 旋转作图的一般步骤:
(1)确定旋转中心、旋转方向和旋转角 .
(2)找出图形的关键点,一般是图形中的转折点 .
(3)作旋转后的对应点,方法如下:
①连: 连接图形的每个关键点与旋转中心;
②转: 把连线绕旋转中心按旋转方向旋转相同的角度(作旋转角) ;
感悟新知
③截: 在作得的角的另一边截取与关键点到旋转中心的距离相等的线段,得到各个关键点的对应点 .
(4) 按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形 .
(5)写出结论,说明作出的图形即为所求作的图形 .
感悟新知
易错点拨
画旋转图形时容易忽视对旋转方向的要求,除了旋转中心及旋转角之外,还应指明旋转方向是顺时针还是逆时针,若无特别说明,则应考虑两种情况 .
感悟新知
如图 5.2 - 5,三角形 ABC 绕点 O 旋转,使点 A 旋转到点 D 处,画出顺时针旋转后的三角形,并写出简要作法.
例3
感悟新知
解题秘方:在旋转作图时,要紧扣以下三点: (1)对应点到旋转中心的距离相等; (2)旋转的角度相等; (3)旋转的方向相同 .
感悟新知
解: 如图 5.2 - 6. 作法: (1)连接 OA, OB, OC, OD;
(2)分别以 OB, OC 为边作∠ BOM= ∠ CON= ∠ AOD;
(3)分别在 OM, ON 上截取 OE=OB, OF=OC;
(4)依次连接DE, EF, FD,三角形DEF就是所求作的三角形.
感悟新知
解法提醒
◆为了避免作图混乱,也可以对一个关键点 连、 转、 截, 找到其对应点后再进行下一个关键点的旋转;
◆已知旋转中心和一组对应点,画旋转图形时要先将这组对应点与旋转中心相连,找出旋转方向和旋转角. 由此将此类问题转化成已知旋转三要素的旋转作图.
旋转
定义
三要素
旋转
性质
作图
旋转角
旋转中心
旋转方向
完成教材课后作业
作业提升
5.2 旋转
第五章 轴对称与旋转
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
旋转的相关概念
旋转的性质
旋转作图
感悟新知
知识点
旋转的相关概念
1
1.图形旋转的概念:
将一个平面图形上的每一个点,绕这个平面内一定点旋转同一个角α (即把图形上每一个点与定点的连线绕定点旋转角α ) ,得到新图形,图形的这种变换叫做旋转 .
此处旋转是指平面内的变换,因此,“平
面内”这一条件不可忽略 .
感悟新知
特别提醒
1. 旋转中心可以是图形外的一点,也可以是图形上的一点,还可以是图形内的一点 .
2. 旋转方向可以是顺时针方向,也可以是逆
时针方向 .
3. 某些特殊图形经过旋转变换后得到的新图形可以与原图形重合,如圆绕圆心旋转任意角度还是原位置的圆 .
感悟新知
2.图形旋转的三要素:
旋转中心 旋转过程中的定点,即不动的点,如右图中的定点 O
旋转角 转动的角(在本书中,旋转角不大于360°),如右图中的∠ POP′ 旋转方向 顺时针或逆时针,如右图中时针的旋转方向为顺时针 感悟新知
3. 图形旋转中的对应元素(如图 5.2 - 1 )
感悟新知
如图 5.2 - 2, A, B, C 三点共线,三角形 ACD 和三角形 BCE 都是等边三角形,三角形 ACE 经过旋转后到达三角形 DCB 的位置 .
(1)旋转中心是哪一点?
(2)旋转角是多少度?
例1
感悟新知
解题秘方:紧扣“图形旋转时,固定不动的点是旋转中心,转动的角是旋转角”进行判断 .
感悟新知
解: (1)点 C 是在三角形 ACE 旋转过程中不动的点,
所以点 C 是旋转中心 .
(2)三角形 ACE 旋转后到达三角形 DCB 的位置, AC 绕点 C 旋转到 DC, AC 转过的角即∠ ACD 就是旋转角 .
因为三角形 ACD 是等边三角形,
所以∠ ACD=60°,即旋转角是 60° .
感悟新知
解法提醒
三角形 ACE 经过旋转后得到三角形DCB.
(1)三角形在旋转过程中不动的点是旋转中心;
(2)两个三角形的对应边所夹的角即为旋转角.
感悟新知
知识点
测量质量
2
一个图形和它经过旋转所得到的图形中,具有如下性质:
(1)对应点到旋转中心的距离相等 .
(2)两组对应点分别与旋转中心的连线所成的角相等 .
(3)旋转不改变图形的形状和大小 .
感悟新知
如图 5.2 - 3, 将三角形 ABC 绕点 O 逆时针旋转 60°得到三角形 A′ B′ C′,则三角形 ABC 能与三角形 A′ B′ C′完全重合 . 对应线段 AB=A′ B′, BC=B′ C′, CA=C′ A′;对应角∠ A= ∠ A′,∠ B= ∠ B′,∠ C= ∠ C′ .
感悟新知
在图 5.2 - 3 中, 对 应 点 A, A ′与 点 O 的 距 离 相 等, 即AO=A ′ O. 类 似 地, BO=B ′ O, CO=C ′ O, 对 应 点 A, A ′与 B, B′与旋转中心的连线所成的角相等,且等于旋转角,即∠ AOA′ = ∠ BOB′ =60° .
感悟新知
特别提醒
1. 要注意区分旋转角与对应角、对应点到旋转中心的距离与对应线段的长度 . 旋转角是指图形旋转过的角度,而非图形中的角度,对应角是指图形旋转前、后能够互相重合的角,是图形中的角;对应点到旋转中心的距离是图形上的点到旋转中心的距离,对应线段的长度则是图形的边长 .
感悟新知
2. 在旋转形成的图形中,找相等的线段一般包含两类:
①旋转前后图形中的对应线段;②各对应点到旋转中心的距离 .
找相等的角也包含两类:
①旋转前后图形中的对应角;②各对应点与旋转中心的连线的夹角 .
感悟新知
如图5.2 - 4, 在正方形 ABCD 中,点 E 在 BC 上,∠ FDE=45°,三角形 DEC 按顺时针方向旋转一个角度后到达三角形 DGA 的位置 .
例2
感悟新知
解题秘方:紧扣旋转的性质解答相关问题 .
感悟新知
(1)图中哪一个点是旋转中心?旋转角是多少度?
解:图中的点 D 是旋转中心,旋转角是 90° .
感悟新知
(2)请写出图中旋转图形的对应线段与对应角 .
解:图中 DE 与 DG, DC 与 DA, EC与 GA 是对应线段;
∠ CDE 与 ∠ ADG, ∠ C 与 ∠ DAG,
∠ DEC 与∠ G 是对应角 .
感悟新知
(3)请写出图中除正方形的四条边、直角外的相等线段与相等角及能够完全重合的三角形 .
解:相等线段: DG=DE, GA=EC;
相 等 角: ∠ G= ∠ DEC= ∠ ADE, ∠ ADG= ∠ CDE,
∠ GDF= ∠ FDE,∠ AFD= ∠ CDF;
能够完全重合的三角形:三角形 DEC 与三角形 DGA.
感悟新知
(4)求∠ GDF 的度数 .
解:因为三角形 DEC 绕点 D 顺时针旋转 90°到三角形DGA 的位置,
所以∠ GDE=90° .
所以∠ GDF= ∠ GDE - ∠ FDE=90° - 45° =45° .
感悟新知
解题通法
由于旋转前后两个图形的形状、大小未发生改变,所以我们在利用旋转来解决与其相关的问题时应抓住以下三点:
1. 明确旋转中的“变” 与“不变”;
2. 找准旋转前后的“对应关系”,正确判断旋转前后图形的对应点、对应角、对应线段以及旋转角,这是理解和应用旋转特征的基础;
3. 充分挖掘旋转过程中的相等关系.
感悟新知
知识点
旋转作图
3
1. 作图依据:
旋转的性质,即对应点到旋转中心的距离相等,每组对应点都旋转相同的角度 .
感悟新知
2. 旋转作图的一般步骤:
(1)确定旋转中心、旋转方向和旋转角 .
(2)找出图形的关键点,一般是图形中的转折点 .
(3)作旋转后的对应点,方法如下:
①连: 连接图形的每个关键点与旋转中心;
②转: 把连线绕旋转中心按旋转方向旋转相同的角度(作旋转角) ;
感悟新知
③截: 在作得的角的另一边截取与关键点到旋转中心的距离相等的线段,得到各个关键点的对应点 .
(4) 按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形 .
(5)写出结论,说明作出的图形即为所求作的图形 .
感悟新知
易错点拨
画旋转图形时容易忽视对旋转方向的要求,除了旋转中心及旋转角之外,还应指明旋转方向是顺时针还是逆时针,若无特别说明,则应考虑两种情况 .
感悟新知
如图 5.2 - 5,三角形 ABC 绕点 O 旋转,使点 A 旋转到点 D 处,画出顺时针旋转后的三角形,并写出简要作法.
例3
感悟新知
解题秘方:在旋转作图时,要紧扣以下三点: (1)对应点到旋转中心的距离相等; (2)旋转的角度相等; (3)旋转的方向相同 .
感悟新知
解: 如图 5.2 - 6. 作法: (1)连接 OA, OB, OC, OD;
(2)分别以 OB, OC 为边作∠ BOM= ∠ CON= ∠ AOD;
(3)分别在 OM, ON 上截取 OE=OB, OF=OC;
(4)依次连接DE, EF, FD,三角形DEF就是所求作的三角形.
感悟新知
解法提醒
◆为了避免作图混乱,也可以对一个关键点 连、 转、 截, 找到其对应点后再进行下一个关键点的旋转;
◆已知旋转中心和一组对应点,画旋转图形时要先将这组对应点与旋转中心相连,找出旋转方向和旋转角. 由此将此类问题转化成已知旋转三要素的旋转作图.
旋转
定义
三要素
旋转
性质
作图
旋转角
旋转中心
旋转方向
完成教材课后作业
作业提升
