6.2.3向量的数乘运算 课件(共17张PPT)
文档属性
| 名称 | 6.2.3向量的数乘运算 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 04:55:28 | ||
图片预览





文档简介
第6章 平面向量及其应用
6.2.3 向量的数乘运算
教学目标
1、理解向量数乘运算及其几何意义(重点)
2、掌握向量数乘运算的运算律,理解向量的线性运算(难点)
3、向量平面向量共线定理及应用(难点)
温故知新
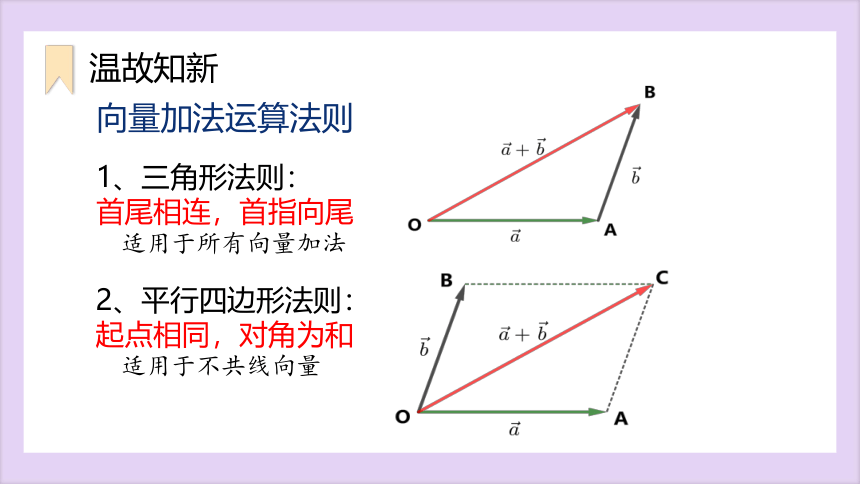
1、三角形法则:
首尾相连,首指向尾
适用于所有向量加法
2、平行四边形法则:
起点相同,对角为和
适用于不共线向量
向量加法运算法则
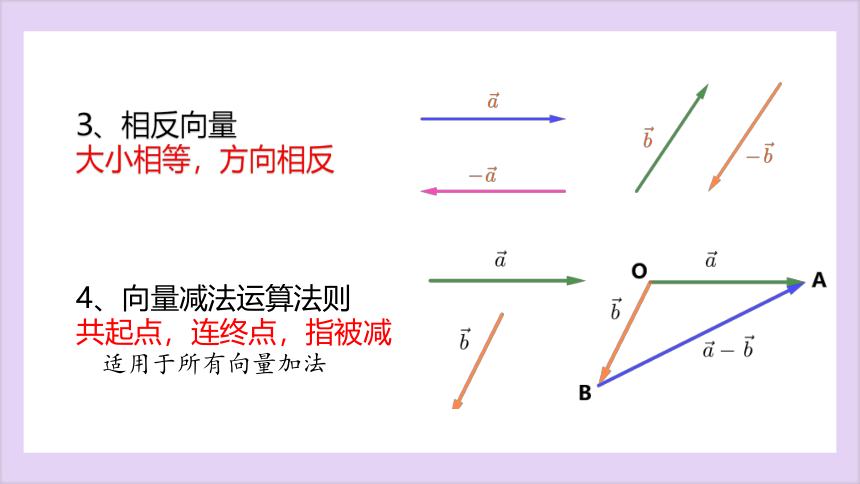
3、相反向量
大小相等,方向相反
4、向量减法运算法则
共起点,连终点,指被减
适用于所有向量加法
“λ”的由来
失意
无奈
孤独
低调
λ
提问
类比引入
竟然数的运算有加减乘除运算,那么向量咱们学了加减法,是否也有对应的乘法和除法运算?
????+????+????记作 ????????,
(?????)+(?????)+(?????)记作?????????
?
显然????????的方向与????的方向相同,
???????? 的长度是????的长度的????倍,
即????????=????????,同样的?????????的长度,也是为????的长度的????倍,即?????????=????????
?
向量的数乘定义
规定实数λ与向量????的积是一个向量,这种运算叫做向量的数乘,记作λ????.
?
生成新知
Ⅰ. ????????长度:????????=????????
?
Ⅱ. ????????方向:①????>0时,与????方向相同
②????<0时,与????方向相反
③????=0时,????????=0;
④????=?1时,????????=(?1)????=?????
?
获得新知
向量的数乘运算律
⑴????(????????)=(????????)????;⑵(????+????)????=????????+????????;
⑶????(????±????)=????????±????????;⑷?????????=?(????????)=????(?????);
⑸????(????1????±????2????)=????????1????±????????2????.
?
当????,????,????????,????????为实数时,有:
?
向量的加、减、数乘运算称为向量的线性运算,向量的线性运算结果仍是向量。
例题解析
例1.计算
⑴(?3)×4????; ⑵3(????+????)?2(?????????)?????;
⑶(2????+3?????????)?(3?????2????+????).
?
解:⑴原式=(?3×4)????=?12????;
⑵原式=3????+3?????2????+2?????????=5????;
⑶原式=2????+3??????????3????+2?????????
=?????+5?????2????.
?
趁热打铁
练习1.计算
⑴5(3?????????)+4(2?????3????);
⑵3(2????+?????3????)?2(?????+?????????);
?
典例解析
例2.如图, ABCD的两条对角线相交于点M,且????????=????,????????=????,用????,????表示????????,????????,????????,????????.
?
再探新知
问题:实数与向量的积与原向量之间有什么位置关系?
结论:
实数与原向量的积与原向量共线
注意:当λ=0时,λ????=0,0与任意向量共线
?
收获新知
由此,我们得到,对于向量????(????≠0)和????,如果有一个实数λ,使????=????????,那么由向量数乘的定义,可知????与????共线;
反之,当????与????共线时,若????≠0,则必然有实数λ,使得????=????????成立.
?
向量共线定理
向量????(????≠0)与????共线的充要条件是:存在唯一一个实数λ,使????=????????.
?
典例解析
例3. 如图已知任意两个非零向量????,????,试作????????=????+????,????????=????+2????,????????=????+3????.猜想A,B,C三点之间的位置关系,并证明你的猜想.
?
解析,具体的作图过程如下:
课堂小结
1.向量的数乘定义
规定实数λ与向量????的积是一个向量,这种运算叫做向量的数乘,记作λ????.
?
λ????与????共线
?
2.向量的加、减、数乘运算称为向量的线性运算,向量的线性运算结果仍是向量。
3.向量共线定理
向量????(????≠0)
????共线的充要条件是:存在唯一一个实数λ, 使????=????????.
?
谢谢观看!
6.2.3 向量的数乘运算
教学目标
1、理解向量数乘运算及其几何意义(重点)
2、掌握向量数乘运算的运算律,理解向量的线性运算(难点)
3、向量平面向量共线定理及应用(难点)
温故知新
1、三角形法则:
首尾相连,首指向尾
适用于所有向量加法
2、平行四边形法则:
起点相同,对角为和
适用于不共线向量
向量加法运算法则
3、相反向量
大小相等,方向相反
4、向量减法运算法则
共起点,连终点,指被减
适用于所有向量加法
“λ”的由来
失意
无奈
孤独
低调
λ
提问
类比引入
竟然数的运算有加减乘除运算,那么向量咱们学了加减法,是否也有对应的乘法和除法运算?
????+????+????记作 ????????,
(?????)+(?????)+(?????)记作?????????
?
显然????????的方向与????的方向相同,
???????? 的长度是????的长度的????倍,
即????????=????????,同样的?????????的长度,也是为????的长度的????倍,即?????????=????????
?
向量的数乘定义
规定实数λ与向量????的积是一个向量,这种运算叫做向量的数乘,记作λ????.
?
生成新知
Ⅰ. ????????长度:????????=????????
?
Ⅱ. ????????方向:①????>0时,与????方向相同
②????<0时,与????方向相反
③????=0时,????????=0;
④????=?1时,????????=(?1)????=?????
?
获得新知
向量的数乘运算律
⑴????(????????)=(????????)????;⑵(????+????)????=????????+????????;
⑶????(????±????)=????????±????????;⑷?????????=?(????????)=????(?????);
⑸????(????1????±????2????)=????????1????±????????2????.
?
当????,????,????????,????????为实数时,有:
?
向量的加、减、数乘运算称为向量的线性运算,向量的线性运算结果仍是向量。
例题解析
例1.计算
⑴(?3)×4????; ⑵3(????+????)?2(?????????)?????;
⑶(2????+3?????????)?(3?????2????+????).
?
解:⑴原式=(?3×4)????=?12????;
⑵原式=3????+3?????2????+2?????????=5????;
⑶原式=2????+3??????????3????+2?????????
=?????+5?????2????.
?
趁热打铁
练习1.计算
⑴5(3?????????)+4(2?????3????);
⑵3(2????+?????3????)?2(?????+?????????);
?
典例解析
例2.如图, ABCD的两条对角线相交于点M,且????????=????,????????=????,用????,????表示????????,????????,????????,????????.
?
再探新知
问题:实数与向量的积与原向量之间有什么位置关系?
结论:
实数与原向量的积与原向量共线
注意:当λ=0时,λ????=0,0与任意向量共线
?
收获新知
由此,我们得到,对于向量????(????≠0)和????,如果有一个实数λ,使????=????????,那么由向量数乘的定义,可知????与????共线;
反之,当????与????共线时,若????≠0,则必然有实数λ,使得????=????????成立.
?
向量共线定理
向量????(????≠0)与????共线的充要条件是:存在唯一一个实数λ,使????=????????.
?
典例解析
例3. 如图已知任意两个非零向量????,????,试作????????=????+????,????????=????+2????,????????=????+3????.猜想A,B,C三点之间的位置关系,并证明你的猜想.
?
解析,具体的作图过程如下:
课堂小结
1.向量的数乘定义
规定实数λ与向量????的积是一个向量,这种运算叫做向量的数乘,记作λ????.
?
λ????与????共线
?
2.向量的加、减、数乘运算称为向量的线性运算,向量的线性运算结果仍是向量。
3.向量共线定理
向量????(????≠0)
????共线的充要条件是:存在唯一一个实数λ, 使????=????????.
?
谢谢观看!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
