人教版七年级数学下册第7章平面直角坐标系复习练习题(含答案)
文档属性
| 名称 | 人教版七年级数学下册第7章平面直角坐标系复习练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 928.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 16:49:06 | ||
图片预览


文档简介
人教版七年级数学下册第7单元《平面直角坐标系》复习练习题(含答案)
一、单选题
1.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知第三象限的点,那么点P到x轴的距离为( )
A.4 B. C. D.3
3.点M到x轴的距离为3,到y轴的距离为2,且在第二象限内,则点M的坐标为( )
A.(2,) B.(,2) C.(,3) D.(3,)
4.在平面直角坐标系中,下列各点位于第四象限的是( )
A.(-2,3) B.(2,3)
C.(2,-3) D.(-2,-3)
5.点到轴的距离是( )
A.-4 B.3 C.4 D.7
6.在平面直角坐标系中,点位于哪个象限?( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至,则a+b的值为( )
A.2 B.3 C.4 D.5
8.在直角坐标系中,将点(-2, -3)向左平移2个单位长度得到的点的坐标是( )
A.(-2,-5) B.(-4,-3) C.(0,-3) D.(-2,1)
9.如图,若在象棋盘上建立直角坐标系,使“帅”位于点.“馬”位于点,则“兵”位于点( )
A. B.
C. D.
10.在平面直角坐标系中,已知点,将点A向左平移3个单位后,再将它向上平移4个单位,则它的坐标变为( )
A. B. C. D.
11.如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1,作A1关于x轴对称点,再往右平移2个单位得到点A2,…,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A64的坐标为( )
A.(2078,-1) B.(2014 ,-1) C.(2078 ,1) D.(2014 ,1)
12.在平面直角坐标系中,与点关于原点对称的点为,则点的坐标是( )
A. B. C. D.
二、填空题
13.在平面直角坐标系中,将点向右平移2个单位长度得到的点的坐标是______.
14.点P(-3,-5)到x轴距离为______,到y轴距离为_______.
15.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为________.
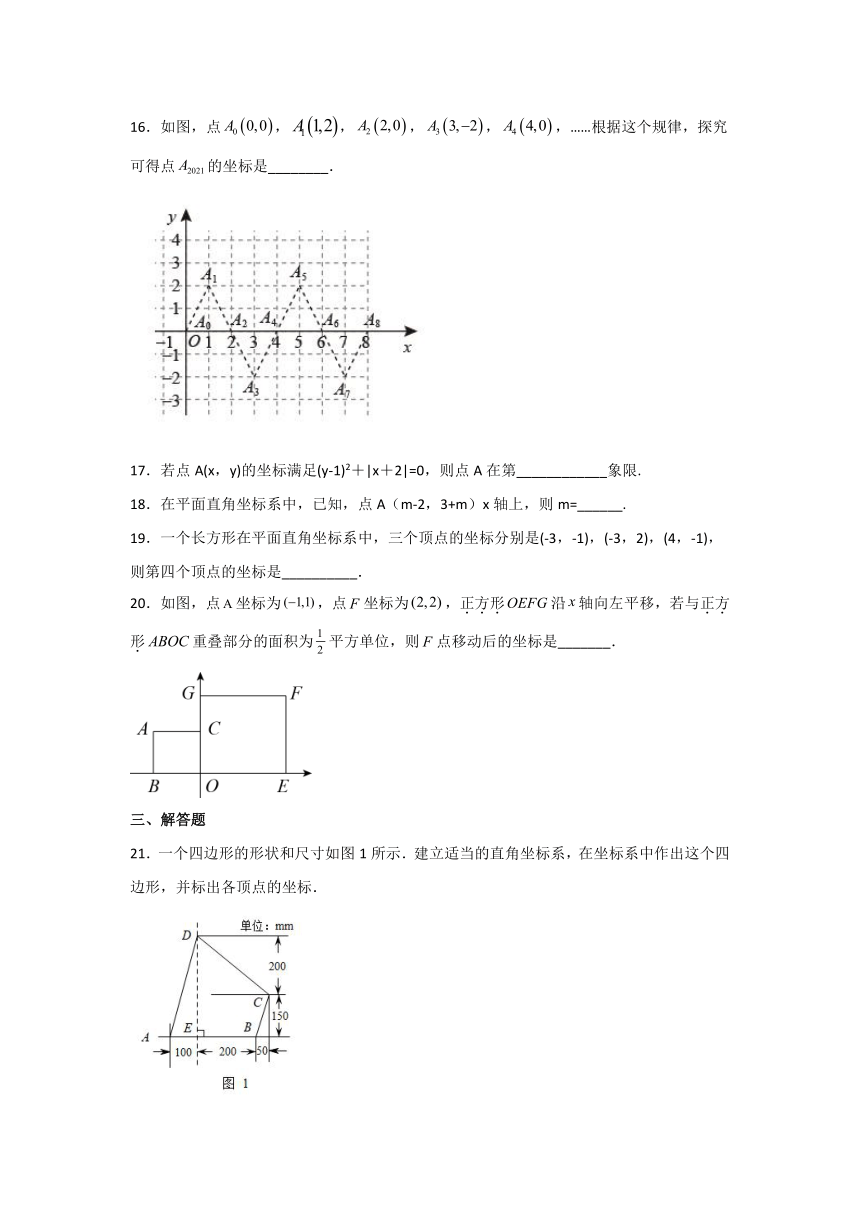
16.如图,点,,,,,……根据这个规律,探究可得点的坐标是________.
17.若点A(x,y)的坐标满足(y-1)2+|x+2|=0,则点A在第____________象限.
18.在平面直角坐标系中,已知,点A(m-2,3+m)x轴上,则m=______.
19.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-3,-1),(-3,2),(4,-1),则第四个顶点的坐标是__________.
20.如图,点坐标为,点坐标为,正方形沿轴向左平移,若与正方形重叠部分的面积为平方单位,则点移动后的坐标是_______.
三、解答题
21.一个四边形的形状和尺寸如图1所示.建立适当的直角坐标系,在坐标系中作出这个四边形,并标出各顶点的坐标.
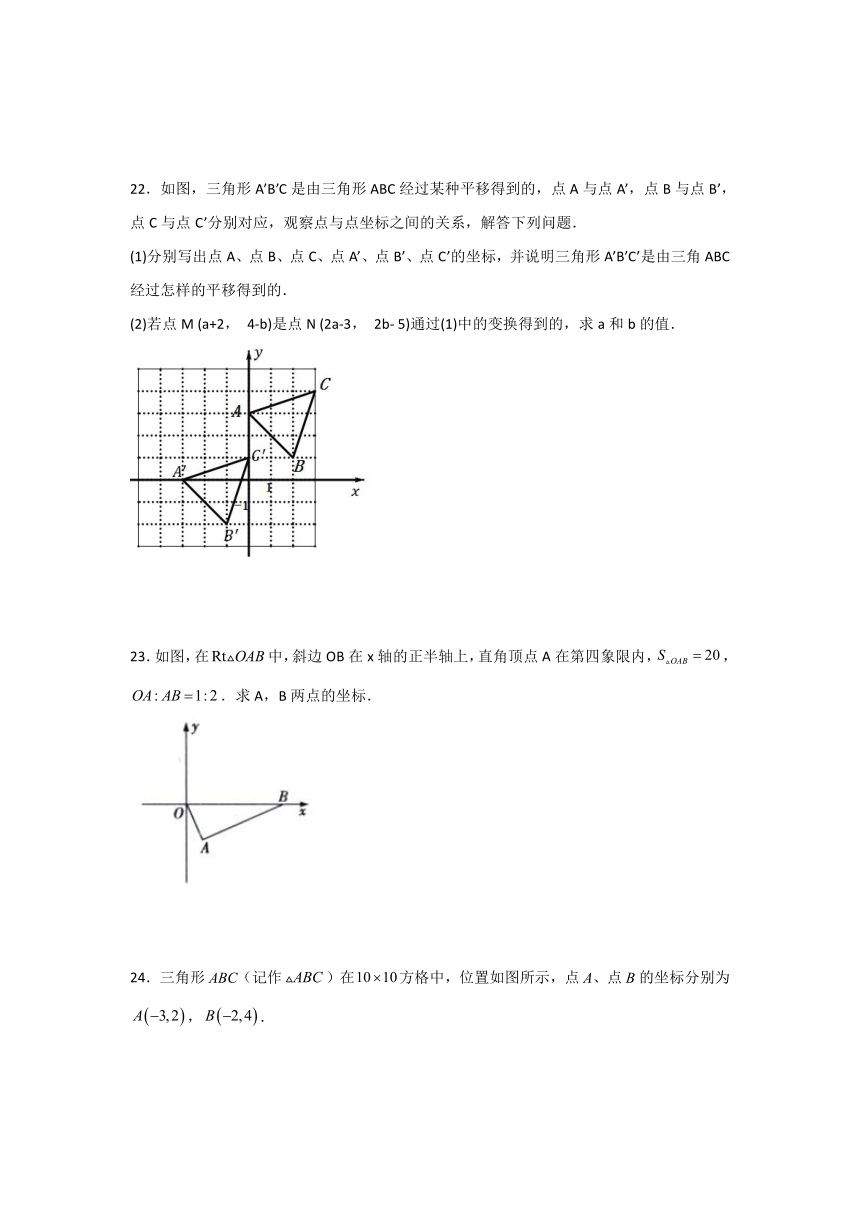
22.如图,三角形A’B’C是由三角形ABC经过某种平移得到的,点A与点A’,点B与点B’,点C与点C’分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)分别写出点A、点B、点C、点A’、点B’、点C’的坐标,并说明三角形A’B’C’是由三角ABC经过怎样的平移得到的.
(2)若点M (a+2, 4-b)是点N (2a-3, 2b- 5)通过(1)中的变换得到的,求a和b的值.
23.如图,在中,斜边OB在x轴的正半轴上,直角顶点A在第四象限内,,.求A,B两点的坐标.
24.三角形ABC(记作)在方格中,位置如图所示,点A、点B的坐标分别为,.
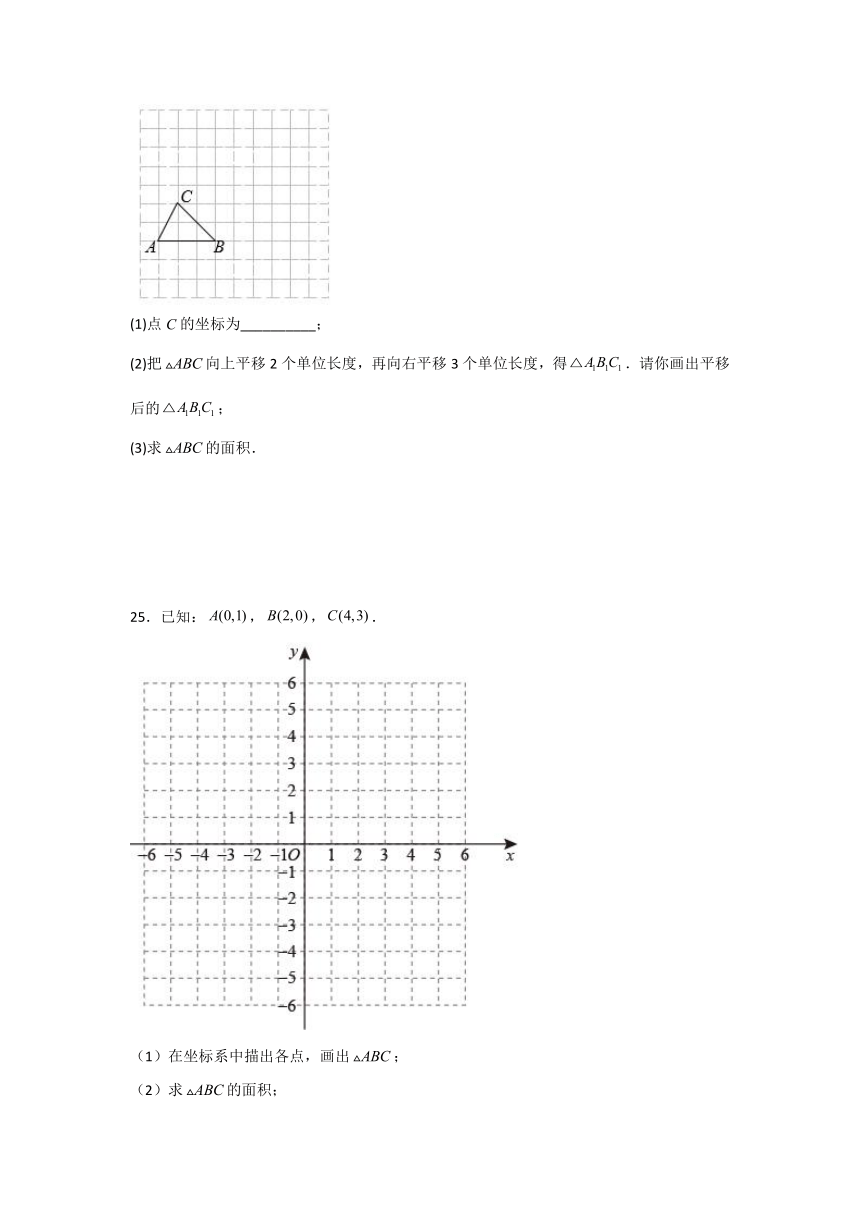
(1)点C的坐标为__________;
(2)把向上平移2个单位长度,再向右平移3个单位长度,得.请你画出平移后的;
(3)求的面积.
25.已知:,,.
(1)在坐标系中描出各点,画出;
(2)求的面积;
(3)设点在坐标轴上,且的面积为面积的两倍,请直接写出符合条件的点的坐标.
26.如图,在平面直角坐标系中,点,点.
(1)将点向右平移个单位长度,再向上平移个单位长度,得到对应点,求的面积;
(2)轴于点,点在直线上,,在图中画出,并直接写出点的坐标.
27.如图①,在平面直角坐标系中,点A,的坐标分别为,,现同时将点A,分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,的对应点,,连接,,.
(1)求,的坐标及;
(2)在轴上是否存在一点,连接,,使,若存在这样一点,求出点的坐标;若不存在,试说明理由;
(3)如图②,点是线段上的一个动点,连接,,当点在上移动时,(不与,重合),求证:.
28.如图1,在平面直角坐标系中,点A、B的坐标分别为A(a,0),B(0,b)=0,现同时将点A、B分别向上平移3个单位长度,再向右平移6个单位,分别得到点A、B的对应点D,C,连接AD,,CD.
(1)求点C,D的坐标;
(2)在y轴上是否存在一点P,使三角形PAC的面积等于四边形ABCD的面积?若存在,请求出点P的坐标,请说明理由;
(3)如图2,设点E是直线CD上一动点(点不与点C、D重合),连接AE、BE,请直接写出,∠CBE和∠AEB之间的数量关系.
参考答案
1.B2.D3.C4.C5.C6.D7.A8.B9.C10.A11.C12.D
13.(4,-5)
14. 5 3
15.(-1,3)
16.
17.二
18.-3
19.(4,2)
20.或
21.解:建立直角坐标系如图2,选择比例为.取点E为直角坐标系的原点,使四边形的边AB在x轴上,则可得A,B,C,D各点的坐标分别为.
根据上述坐标在直角坐标系中作点A,B,C,D,并用线段依次连结备点,如图2中的四边形就是所求作的图形.
22.解:(1)由图可知,A(0,3),B(2,1),C (3,4),A’ (-3,0),B’(-1, -2),C’(0,1),
∴△ABC向左平移3个单位,向下平移3个单位可以得到△A’B’C’.
(2)由(1)中的平移变换的2a-3-3=a+2, 2b-5-3=4-b,解得a=8,b=4.
23.解:过点作,垂足为.
设,则.
,
,即.
解得:.
,.
由勾股定理得:.
点的坐标为.
,
.
.
在中,由勾股定理得:.
点的坐标为,.
24.(1)解:将点向右平移三个单位即可得到点C,坐标为为:,
故答案为:;
(2)解:把向上平移2个单位长度,再向右平移3个单位长度,得,如下图:
(3)解:的面积.
25.解:(1)如图所示;
(2)作轴于,轴于.
.
(3)当点在轴上时,的面积,
,
或,
当点在轴上时,的面积,
,
或,
综上所述,满足条件的点坐标为或或或.
26.解:(1)点C的坐标为(6,4),
S△ABC=6×4-×4×3-×2×4-×6×1=11;
(2)设E(t,4),
∵S△EAO=S△AOB,
∴×|t|×3=×3×4,解得t=±4,
∴E点坐标为(4,4)或(-4,4),
如图,
27.(1)解:点A,B的坐标分别为(-1,0),(3,0),
将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,
∴点C(0,2),点D(4,2),
OC=2,
∵AB=4,AB//CD,AB=CD,
S四边形ABCD=4×2=8;
(2)
解:设Q坐标为(0,m),
,
,
解得m= 4.
Q点的坐标为(0,4)或(0,-4);
(3)
解:如图,作PE//CD,
由平移可知:CD//AB,
CD//PE//AB.
∠DCP=∠EPC,∠BOP=∠EPO.
∠DCP+∠BOP=∠EPC+∠EPO=∠CPO.
28.(1)=0,,,
解得
将点A、B分别向上平移3个单位长度,再向右平移6个单位,分别得到点A、B的对应点D,C,
由平移的性质可知,即将A、B的横坐标+6,纵坐标+3,
,
即;
(2)存在,理由如下:
设,,,
,
三角形PAC的面积为,
四边形ABCD的面积为,
,
解得,
或者;
(3)如图,过点作,
,
平移后对应的点分别为,
,
,
,
,
.
.
一、单选题
1.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知第三象限的点,那么点P到x轴的距离为( )
A.4 B. C. D.3
3.点M到x轴的距离为3,到y轴的距离为2,且在第二象限内,则点M的坐标为( )
A.(2,) B.(,2) C.(,3) D.(3,)
4.在平面直角坐标系中,下列各点位于第四象限的是( )
A.(-2,3) B.(2,3)
C.(2,-3) D.(-2,-3)
5.点到轴的距离是( )
A.-4 B.3 C.4 D.7
6.在平面直角坐标系中,点位于哪个象限?( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至,则a+b的值为( )
A.2 B.3 C.4 D.5
8.在直角坐标系中,将点(-2, -3)向左平移2个单位长度得到的点的坐标是( )
A.(-2,-5) B.(-4,-3) C.(0,-3) D.(-2,1)
9.如图,若在象棋盘上建立直角坐标系,使“帅”位于点.“馬”位于点,则“兵”位于点( )
A. B.
C. D.
10.在平面直角坐标系中,已知点,将点A向左平移3个单位后,再将它向上平移4个单位,则它的坐标变为( )
A. B. C. D.
11.如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1,作A1关于x轴对称点,再往右平移2个单位得到点A2,…,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A64的坐标为( )
A.(2078,-1) B.(2014 ,-1) C.(2078 ,1) D.(2014 ,1)
12.在平面直角坐标系中,与点关于原点对称的点为,则点的坐标是( )
A. B. C. D.
二、填空题
13.在平面直角坐标系中,将点向右平移2个单位长度得到的点的坐标是______.
14.点P(-3,-5)到x轴距离为______,到y轴距离为_______.
15.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为________.
16.如图,点,,,,,……根据这个规律,探究可得点的坐标是________.
17.若点A(x,y)的坐标满足(y-1)2+|x+2|=0,则点A在第____________象限.
18.在平面直角坐标系中,已知,点A(m-2,3+m)x轴上,则m=______.
19.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-3,-1),(-3,2),(4,-1),则第四个顶点的坐标是__________.
20.如图,点坐标为,点坐标为,正方形沿轴向左平移,若与正方形重叠部分的面积为平方单位,则点移动后的坐标是_______.
三、解答题
21.一个四边形的形状和尺寸如图1所示.建立适当的直角坐标系,在坐标系中作出这个四边形,并标出各顶点的坐标.
22.如图,三角形A’B’C是由三角形ABC经过某种平移得到的,点A与点A’,点B与点B’,点C与点C’分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)分别写出点A、点B、点C、点A’、点B’、点C’的坐标,并说明三角形A’B’C’是由三角ABC经过怎样的平移得到的.
(2)若点M (a+2, 4-b)是点N (2a-3, 2b- 5)通过(1)中的变换得到的,求a和b的值.
23.如图,在中,斜边OB在x轴的正半轴上,直角顶点A在第四象限内,,.求A,B两点的坐标.
24.三角形ABC(记作)在方格中,位置如图所示,点A、点B的坐标分别为,.
(1)点C的坐标为__________;
(2)把向上平移2个单位长度,再向右平移3个单位长度,得.请你画出平移后的;
(3)求的面积.
25.已知:,,.
(1)在坐标系中描出各点,画出;
(2)求的面积;
(3)设点在坐标轴上,且的面积为面积的两倍,请直接写出符合条件的点的坐标.
26.如图,在平面直角坐标系中,点,点.
(1)将点向右平移个单位长度,再向上平移个单位长度,得到对应点,求的面积;
(2)轴于点,点在直线上,,在图中画出,并直接写出点的坐标.
27.如图①,在平面直角坐标系中,点A,的坐标分别为,,现同时将点A,分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,的对应点,,连接,,.
(1)求,的坐标及;
(2)在轴上是否存在一点,连接,,使,若存在这样一点,求出点的坐标;若不存在,试说明理由;
(3)如图②,点是线段上的一个动点,连接,,当点在上移动时,(不与,重合),求证:.
28.如图1,在平面直角坐标系中,点A、B的坐标分别为A(a,0),B(0,b)=0,现同时将点A、B分别向上平移3个单位长度,再向右平移6个单位,分别得到点A、B的对应点D,C,连接AD,,CD.
(1)求点C,D的坐标;
(2)在y轴上是否存在一点P,使三角形PAC的面积等于四边形ABCD的面积?若存在,请求出点P的坐标,请说明理由;
(3)如图2,设点E是直线CD上一动点(点不与点C、D重合),连接AE、BE,请直接写出,∠CBE和∠AEB之间的数量关系.
参考答案
1.B2.D3.C4.C5.C6.D7.A8.B9.C10.A11.C12.D
13.(4,-5)
14. 5 3
15.(-1,3)
16.
17.二
18.-3
19.(4,2)
20.或
21.解:建立直角坐标系如图2,选择比例为.取点E为直角坐标系的原点,使四边形的边AB在x轴上,则可得A,B,C,D各点的坐标分别为.
根据上述坐标在直角坐标系中作点A,B,C,D,并用线段依次连结备点,如图2中的四边形就是所求作的图形.
22.解:(1)由图可知,A(0,3),B(2,1),C (3,4),A’ (-3,0),B’(-1, -2),C’(0,1),
∴△ABC向左平移3个单位,向下平移3个单位可以得到△A’B’C’.
(2)由(1)中的平移变换的2a-3-3=a+2, 2b-5-3=4-b,解得a=8,b=4.
23.解:过点作,垂足为.
设,则.
,
,即.
解得:.
,.
由勾股定理得:.
点的坐标为.
,
.
.
在中,由勾股定理得:.
点的坐标为,.
24.(1)解:将点向右平移三个单位即可得到点C,坐标为为:,
故答案为:;
(2)解:把向上平移2个单位长度,再向右平移3个单位长度,得,如下图:
(3)解:的面积.
25.解:(1)如图所示;
(2)作轴于,轴于.
.
(3)当点在轴上时,的面积,
,
或,
当点在轴上时,的面积,
,
或,
综上所述,满足条件的点坐标为或或或.
26.解:(1)点C的坐标为(6,4),
S△ABC=6×4-×4×3-×2×4-×6×1=11;
(2)设E(t,4),
∵S△EAO=S△AOB,
∴×|t|×3=×3×4,解得t=±4,
∴E点坐标为(4,4)或(-4,4),
如图,
27.(1)解:点A,B的坐标分别为(-1,0),(3,0),
将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,
∴点C(0,2),点D(4,2),
OC=2,
∵AB=4,AB//CD,AB=CD,
S四边形ABCD=4×2=8;
(2)
解:设Q坐标为(0,m),
,
,
解得m= 4.
Q点的坐标为(0,4)或(0,-4);
(3)
解:如图,作PE//CD,
由平移可知:CD//AB,
CD//PE//AB.
∠DCP=∠EPC,∠BOP=∠EPO.
∠DCP+∠BOP=∠EPC+∠EPO=∠CPO.
28.(1)=0,,,
解得
将点A、B分别向上平移3个单位长度,再向右平移6个单位,分别得到点A、B的对应点D,C,
由平移的性质可知,即将A、B的横坐标+6,纵坐标+3,
,
即;
(2)存在,理由如下:
设,,,
,
三角形PAC的面积为,
四边形ABCD的面积为,
,
解得,
或者;
(3)如图,过点作,
,
平移后对应的点分别为,
,
,
,
,
.
.
