第28章 锐角三角函数(训练题)(无答案)2022—2023学年人教版数学九年级下册
文档属性
| 名称 | 第28章 锐角三角函数(训练题)(无答案)2022—2023学年人教版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 680.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 17:01:48 | ||
图片预览

文档简介
第28章 锐角三角函数(训练题)-人教版九年级下册
一.选择题
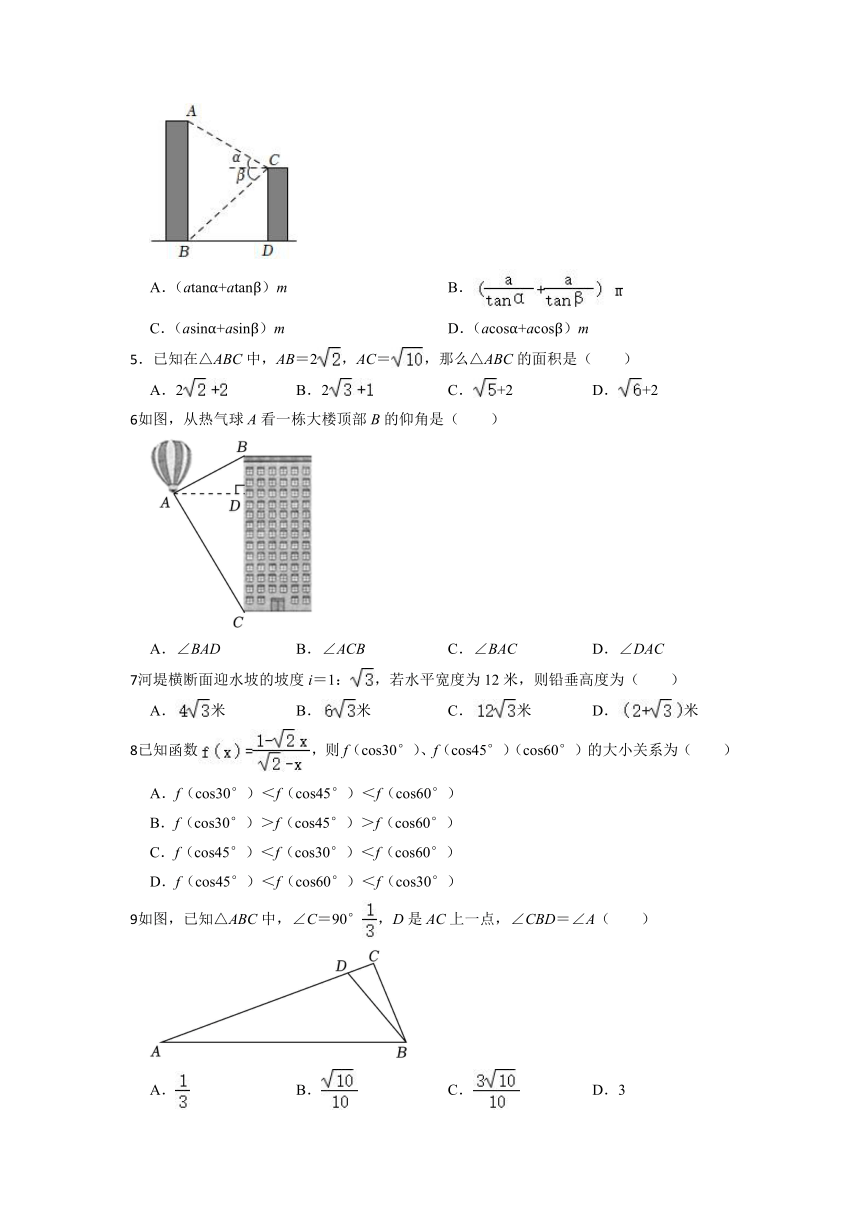
.某游乐场一个不等臂跷跷板AB长5.6米,支撑柱OH垂直地面,如图1,AB与地面的夹角的正切值为;如图2,AB与地面夹角的正弦值为,则支撑柱OH的长为( )
A.0.4 米 B.0.8 米 C.米 D.1.2 米
.如图,Rt△ABC中,,点D是边BC的中点,使∠ADE=∠B,连结CE,则( )
A.2 B. C. D.
.如图,两根木条钉成一个角形框架∠AOB,且∠AOB=120°,将一根橡皮筋两端固定在点A,B处,在平面内,拉动橡皮筋上的一点C,橡皮筋再次被拉长了( )
A.2cm B.4cm C. D.
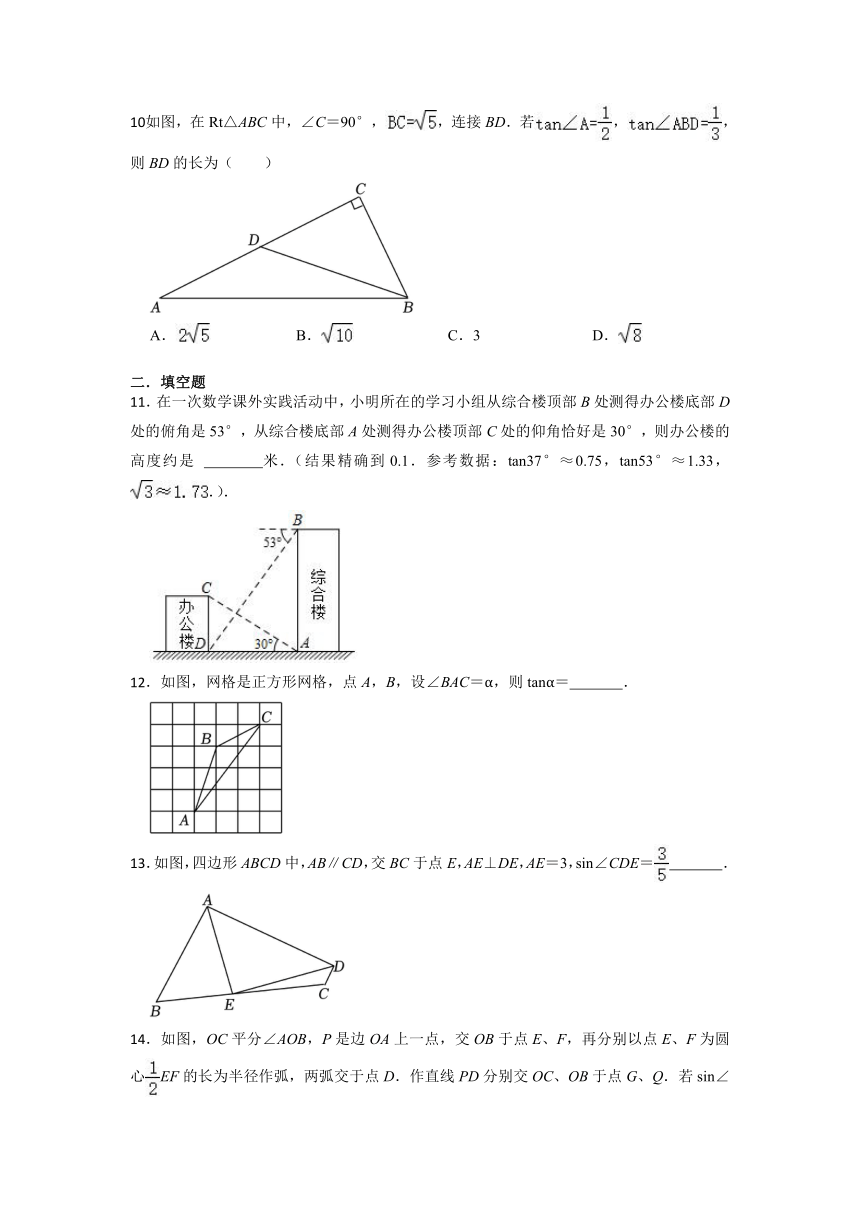
.如图,某校教学楼AB与CD的水平间距BD=am,在教学楼CD的顶部C点测得教学楼AB的顶部A点的仰角为α,则教学楼AB的高度是( )
A.(atanα+atanβ)m B.
C.(asinα+asinβ)m D.(acosα+acosβ)m
.已知在△ABC中,AB=2,AC=,那么△ABC的面积是( )
A.2 B.2 C.+2 D.+2
如图,从热气球A看一栋大楼顶部B的仰角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
河堤横断面迎水坡的坡度i=1:,若水平宽度为12米,则铅垂高度为( )
A.米 B.米 C.米 D.米
已知函数,则f(cos30°)、f(cos45°)(cos60°)的大小关系为( )
A.f(cos30°)<f(cos45°)<f(cos60°)
B.f(cos30°)>f(cos45°)>f(cos60°)
C.f(cos45°)<f(cos30°)<f(cos60°)
D.f(cos45°)<f(cos60°)<f(cos30°)
如图,已知△ABC中,∠C=90°,D是AC上一点,∠CBD=∠A( )
A. B. C. D.3
如图,在Rt△ABC中,∠C=90°,,连接BD.若,,则BD的长为( )
A. B. C.3 D.
二.填空题
.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,则办公楼的高度约是 米.(结果精确到0.1.参考数据:tan37°≈0.75,tan53°≈1.33,.).
.如图,网格是正方形网格,点A,B,设∠BAC=α,则tanα= .
.如图,四边形ABCD中,AB∥CD,交BC于点E,AE⊥DE,AE=3,sin∠CDE= .
.如图,OC平分∠AOB,P是边OA上一点,交OB于点E、F,再分别以点E、F为圆心EF的长为半径作弧,两弧交于点D.作直线PD分别交OC、OB于点G、Q.若sin∠AOB=,则△OPG的面积为 .
.台灯,是我们在学习中的万能“小助手”.如图1是一盏可调节台灯,图2和图3为示意图,AB为固定支撑杆,BC为可绕着点B旋转的调节杆,MN为台灯照射在桌面的区域,如图2,已知此时DM=DN,tan∠B=,AB=5dm,BC=7dm,则cos∠DME的值为 .
三.解答题
.如图,已知在△ABC中,CD⊥AB,AD=2,BD=6,点E是边BC的中点.
(1)求边AC的长;
(2)求∠EAB的正弦值.
.“太阳鸟”是某市文化广场的标志性雕塑.某“数学综合与实践”小组为了测量“太阳鸟”的高度,利用双休日通过实地测量(如示意图)和查阅资料
信息一:在H处用高1.5米的测角仪BH,测得最高点A的仰角为30°.
信息二:在F处用同一测角仪测得最高点A的仰角为45°.
信息三:测得FH=25米,点D、F、H在同一条直线上.
请根据以上信息,回答下列问题:
(1)在Rt△ACB中,= (填sin30°、cos30或tan30°),∴= .
(2)设AC=x米,则CE= 米(用含x的代数式表示)米,BC= 米(用含x的代数式表示).
(3)“太阳鸟”的高度AD约为多少米?(精确到0.1,≈1.73)
.如图,在△ABC中,∠C=90°,点E是BC边上一个动点(点E与A、C不重合),连接B,且c是不等式组的整数解.
(1)求a、b、c的长;
(2)当AE平分△ABC的周长时,此时AE是否平分△ABC的面积?
.如图,在Rt△ABC中,∠C=90°,AD=BD=5,sin∠ADC=.
(1)求cot∠BAD的值;
(2)如果边AB的中点为M,联结CM,交AD于E
.钓鱼是修身养性的户外休闲运动,闲暇之余,流连于江河湖泊之间,玉树葱葱,享受大自然,“劝君莫食三月鲫,万千鱼仔鱼腹中”,钓获放流是一种境界!
如图一静待鲤鱼上钩:AB是鱼竿,BC、CD是鱼线,EH是水面,AF⊥EH,AB=8米,CH=0.5米,∠ABE=30°
如图二扬竿中鱼:鱼竿AB弯成圆弧,其圆心恰好是点O,鱼线OB由于受到拉力作用,即:OB=1.2(BC+CD).
若∠AOB的度数超过45°,鱼竿将有折断的危险,请你通过计算说明:是否有断竿跑鱼的危险?
(参考数据:π取3,sin4.4°≈,cos4.4°≈0.997,tan4.4°≈3.096)
一.选择题
.某游乐场一个不等臂跷跷板AB长5.6米,支撑柱OH垂直地面,如图1,AB与地面的夹角的正切值为;如图2,AB与地面夹角的正弦值为,则支撑柱OH的长为( )
A.0.4 米 B.0.8 米 C.米 D.1.2 米
.如图,Rt△ABC中,,点D是边BC的中点,使∠ADE=∠B,连结CE,则( )
A.2 B. C. D.
.如图,两根木条钉成一个角形框架∠AOB,且∠AOB=120°,将一根橡皮筋两端固定在点A,B处,在平面内,拉动橡皮筋上的一点C,橡皮筋再次被拉长了( )
A.2cm B.4cm C. D.
.如图,某校教学楼AB与CD的水平间距BD=am,在教学楼CD的顶部C点测得教学楼AB的顶部A点的仰角为α,则教学楼AB的高度是( )
A.(atanα+atanβ)m B.
C.(asinα+asinβ)m D.(acosα+acosβ)m
.已知在△ABC中,AB=2,AC=,那么△ABC的面积是( )
A.2 B.2 C.+2 D.+2
如图,从热气球A看一栋大楼顶部B的仰角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
河堤横断面迎水坡的坡度i=1:,若水平宽度为12米,则铅垂高度为( )
A.米 B.米 C.米 D.米
已知函数,则f(cos30°)、f(cos45°)(cos60°)的大小关系为( )
A.f(cos30°)<f(cos45°)<f(cos60°)
B.f(cos30°)>f(cos45°)>f(cos60°)
C.f(cos45°)<f(cos30°)<f(cos60°)
D.f(cos45°)<f(cos60°)<f(cos30°)
如图,已知△ABC中,∠C=90°,D是AC上一点,∠CBD=∠A( )
A. B. C. D.3
如图,在Rt△ABC中,∠C=90°,,连接BD.若,,则BD的长为( )
A. B. C.3 D.
二.填空题
.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,则办公楼的高度约是 米.(结果精确到0.1.参考数据:tan37°≈0.75,tan53°≈1.33,.).
.如图,网格是正方形网格,点A,B,设∠BAC=α,则tanα= .
.如图,四边形ABCD中,AB∥CD,交BC于点E,AE⊥DE,AE=3,sin∠CDE= .
.如图,OC平分∠AOB,P是边OA上一点,交OB于点E、F,再分别以点E、F为圆心EF的长为半径作弧,两弧交于点D.作直线PD分别交OC、OB于点G、Q.若sin∠AOB=,则△OPG的面积为 .
.台灯,是我们在学习中的万能“小助手”.如图1是一盏可调节台灯,图2和图3为示意图,AB为固定支撑杆,BC为可绕着点B旋转的调节杆,MN为台灯照射在桌面的区域,如图2,已知此时DM=DN,tan∠B=,AB=5dm,BC=7dm,则cos∠DME的值为 .
三.解答题
.如图,已知在△ABC中,CD⊥AB,AD=2,BD=6,点E是边BC的中点.
(1)求边AC的长;
(2)求∠EAB的正弦值.
.“太阳鸟”是某市文化广场的标志性雕塑.某“数学综合与实践”小组为了测量“太阳鸟”的高度,利用双休日通过实地测量(如示意图)和查阅资料
信息一:在H处用高1.5米的测角仪BH,测得最高点A的仰角为30°.
信息二:在F处用同一测角仪测得最高点A的仰角为45°.
信息三:测得FH=25米,点D、F、H在同一条直线上.
请根据以上信息,回答下列问题:
(1)在Rt△ACB中,= (填sin30°、cos30或tan30°),∴= .
(2)设AC=x米,则CE= 米(用含x的代数式表示)米,BC= 米(用含x的代数式表示).
(3)“太阳鸟”的高度AD约为多少米?(精确到0.1,≈1.73)
.如图,在△ABC中,∠C=90°,点E是BC边上一个动点(点E与A、C不重合),连接B,且c是不等式组的整数解.
(1)求a、b、c的长;
(2)当AE平分△ABC的周长时,此时AE是否平分△ABC的面积?
.如图,在Rt△ABC中,∠C=90°,AD=BD=5,sin∠ADC=.
(1)求cot∠BAD的值;
(2)如果边AB的中点为M,联结CM,交AD于E
.钓鱼是修身养性的户外休闲运动,闲暇之余,流连于江河湖泊之间,玉树葱葱,享受大自然,“劝君莫食三月鲫,万千鱼仔鱼腹中”,钓获放流是一种境界!
如图一静待鲤鱼上钩:AB是鱼竿,BC、CD是鱼线,EH是水面,AF⊥EH,AB=8米,CH=0.5米,∠ABE=30°
如图二扬竿中鱼:鱼竿AB弯成圆弧,其圆心恰好是点O,鱼线OB由于受到拉力作用,即:OB=1.2(BC+CD).
若∠AOB的度数超过45°,鱼竿将有折断的危险,请你通过计算说明:是否有断竿跑鱼的危险?
(参考数据:π取3,sin4.4°≈,cos4.4°≈0.997,tan4.4°≈3.096)
