欢迎进入几何的殿堂[上学期]

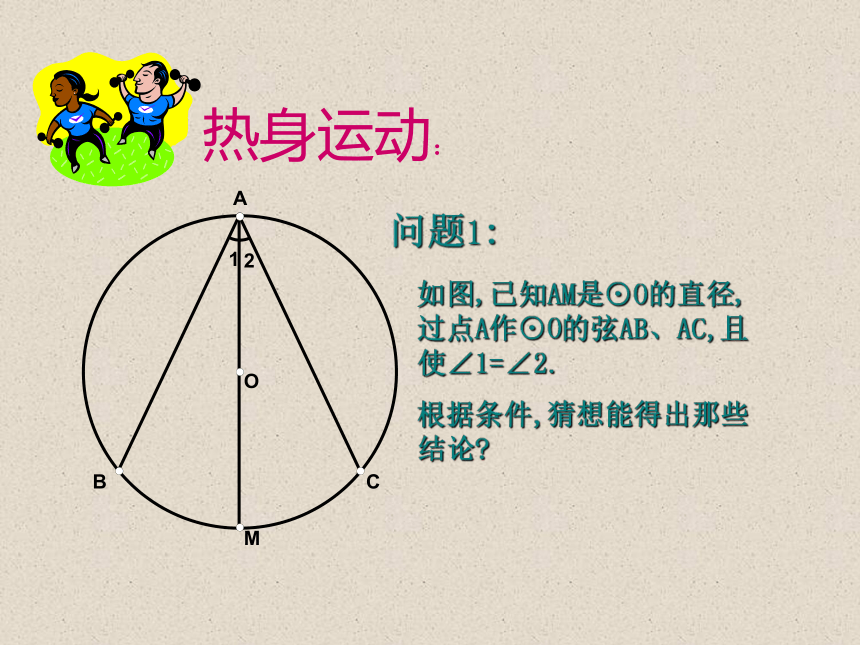
课件9张PPT。利用辅助线解题探究欢迎进入几何的殿堂执教者: 冯妍前 言 通过上一节课的证明举例,我们已经知道对于一些较为复杂的几何问题,可一通过添加辅助线来构造基本图形,使问题得以解决,今天,我们继续通过证明举例,进一步学习添辅助线的方法.热身运动：问题1:如图,已知AM是⊙O的直径,过点A作⊙O的弦AB、AC,且使∠1=∠2.根据条件,猜想能得出那些结论?苦思冥想：?当点A在直径AM上移动时,图形会发生什么样的变化呢?结论还成立吗??当点A在直径MA的延长线上移动时,图形又会发生什么样的变化呢?结论还成立吗??不论过直径(或直径延长线)上的哪一点做两条与圆相交的直线,如果满足所做直线与直径的夹角相等,那么一定有什么结论?这个结论的成立与这个点的位置有什么关系?突发奇想：若将此图中的B、C两点连接,交AM于D点,会有什么新的结论?为什么?挑战自我：如图，已知D是BC上的一点，∠1=∠2 ， BD=CD 。
求证：AB=AC超越自我：如图,已知∠1=∠2,DA=DB,2AC=AB.
求证:DC⊥AC如图,已知CD∥AB,∠D=90°,AB=2CD,
AE⊥BC,CE=BE.
求证:∠1=∠2?超越自我：如图,已知在△ABC中，AB=AC，
延长AB到点D，使BD=AB，
CE为AB的中线。
求证:CD=2CE?小 结辅助线可以通过构造基本图形或利用几何图形的基本性质来添加
利用图形的运动添辅助线,从而把分散的已知条件相对集中,是问题得以解决,这也是一种常用的方法
在解决问题时,我们有时还可以从题目的某些特殊已知条件或结论的特征中得到启发
我们要在学习的过程中善于观察猜想,勤于归纳总结,勇于探索创新