七年级数学《频率的稳定性》课件

课件23张PPT。2 频率的稳定性 1.完成下列问题：
(1)在n次重复试验中，不确定事件A发生了m次，则比值__称为
事件A发生的频率.
(2)在试验次数很大时，某一事件发生的频率，都会在一个
_____附近摆动，这个性质称为频率的_______.
(3)抛掷一枚均匀的硬币，落地后，正面朝上或正面朝下的可能
性_____. 常数稳定性相同2.概率.
(1)定义：刻画事件A发生的___________的数值，称为事件A发
生的概率，记为P(A).
(2)取值：必然事件发生的概率为__，不可能事件发生的概率为
__，不确定事件发生的概率是__到__之间的一个常数.可能性大小1001【预习思考】
小明经过50次试验，求得某一事件发生的频率为0.8，由此他判断该事件发生的概率为0.8，对吗？
提示：不正确，由频率估计概率，需要大量的试验，仅仅50次，不足以说明. 用频率估计概率
【例】(8分)(2012·青岛中考)某商场为了吸引顾客，举行抽奖活动，并规定：顾客每购买100元的商品，就可随机抽取一张奖券，抽得奖券“紫气东来”“花开富贵”“吉星高照”，就可以分别获得100元、50元、20元的购物券，抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖，可以直接获得购物券10元.小明购买了100元的商品，他看到商场公布的前10 000张奖券的抽奖结果如下：(1)求“紫气东来”奖券出现的频率.
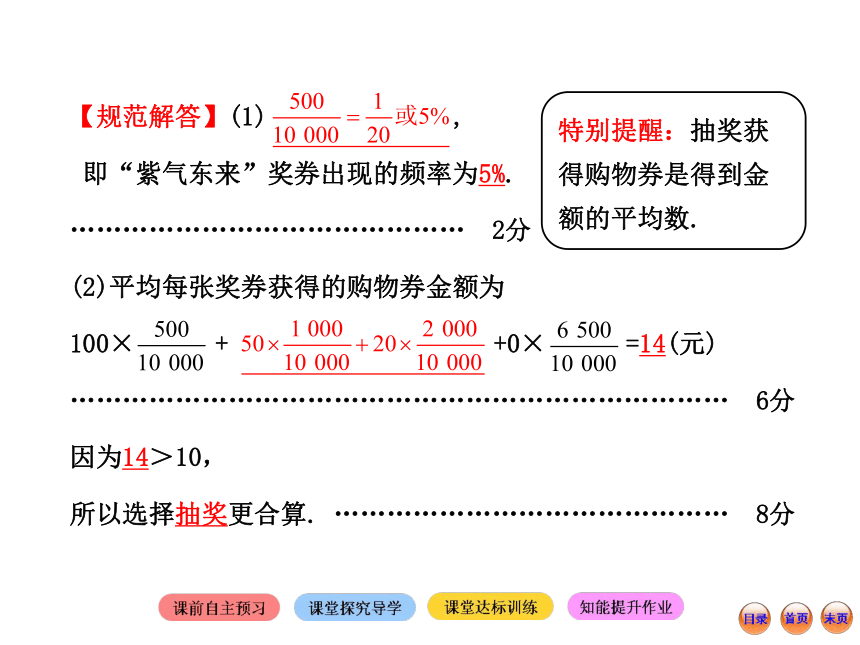
(2)请你帮助小明判断，抽奖和直接获得购物券，哪种方式更合算？并说明理由.【规范解答】(1) ,
即“紫气东来”奖券出现的频率为5%.
……………………………………… 2分
(2)平均每张奖券获得的购物券金额为
100× + +0× =14(元)
………………………………………………………………… 6分
因为14＞10，
所以选择抽奖更合算. ……………………………………… 8分特别提醒：抽奖获得购物券是得到金额的平均数. 【规律总结】
根据频率求概率要找准两点
(1)符合条件的情况数目.(2)全部情况的总数.
二者的比值就是其发生的概率. 【跟踪训练】
1. 做重复试验：抛掷同一枚啤酒瓶盖1 000次.经过统计得“凸面向上”的频率约为0.44，则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
(A)0.22 (B)0.44 (C)0.50 (D)0.56
【解析】选D.瓶盖只有两面，“凸面向上”的频率约为0.44，则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为1-0.44=0.56.2. 小明练习射击，共射击60次，其中有38次击中靶子，由此可估计，小明射击一次击中靶子的概率( )
(A)38% (B)60%
(C)约63% (D)无法确定
【解析】选C.因为小明练习射击，共射击60次，其中有38次击中靶子，所以射中靶子的频率=38÷60≈0.63，故小明射击一次击中靶子的概率约63%.3.在一个不透明的布袋中，红色、黑色、白色的球共有120个，除颜色外，形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在15%和45%，则口袋中白色球的个数很可能是( )
(A)48个 (B)60个 (C)18个 (D)54个
【解析】选A.设红球有x个，黑球有y个，由题意得：x∶120=15%,y∶120=45%,解得x=18，y=54，所以白球数=120-18-54=48(个).【变式备选】一个密闭不透明的盒子里有若干个白球，在不允
许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8
个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒
中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大
约有白球( )
(A)28个 (B)30个 (C)36个 (D)42个
【解析】选A.由题意得：白球有 ×8≈28(个).1. 下列说法正确的是 ( )
某事件发生的概率为 ，这就是说：在两次重复试验中，
必有一次发生
(B)一个袋子里有100个球，小明摸了8次，每次都只摸到黑球，
没摸到白球，结论：袋子里只有黑色的球
(C)两枚一元的硬币同时抛下，可能出现的情形有：①两枚均为
正面；②两枚均为反面；③一正面一反面，所以出现一正面一
反面的概率是
(D)全年级有367名同学，一定会有2人同一天过生日【解析】选D.“当试验次数很大时，试验频率稳定于理论概
率”并不意味着，试验次数越大，就越为靠近.应该说，作为一
个整体趋势，上述结论是正确的，而不是某事件的概率为 ，
在两次重复试验中,就一定有一次发生.因此A不正确，B也不正
确.而对于C,两枚硬币同时抛下，出现一正面一反面的概率
为 ，即 .对于D，由367＞366，可知必有两人生日相同.2. (2012·贵阳中考)一个不透明的盒子里有n个除颜色外其他
完全相同的小球，其中有6个黄球.每次摸球前先将盒子里的球
摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复
摸球试验后发现，摸到黄球的频率稳定在30%，那么可以推算出
n大约是( )
(A)6 (B)10 (C)18 (D)20
【解析】选D.由题意可得， ×100%=30%，解得n=20.故估计n
大约是20.3.在创建国家生态园林城市活动中，某市园林部门为了扩大城市的绿化面积.进行了大量的树木移栽.下表记录的是在相同的条件下移栽某种幼树的棵数与成活棵树：依此估计这种幼树成活的概率是_______.(结果用小数表示，精确到0.1)
【解析】根据抽样的意义可得幼树成活的概率为
(89+910+9 008)÷(100+1 000+10 000)≈0.9.
答案：0.94. 在对某次试验数据整理过程中，某个事件出现的频率随试验次数变化折线图如图所示，这个图形中折线的变化特点是_____
____________，试举一个大致符合这个特点的实物试验的例子(指出关注的结果)_______________.【解析】这个图形中折线的变化特点是随着试验次数增加，频率趋于稳定，符合这个特点的实物试验的例子(指出关注的结果)如抛掷硬币试验中关注正面出现的频率.
答案：随着试验次数增加，频率趋于稳定 如抛掷硬币试验中关注正面出现的频率5. 某商场设计了一个可以自由转动的转盘如图，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据：(1)计算并完成表格：
(2)请估计，当n很大时，频率将会接近多少？【解析】(1)68÷100=0.68，111÷150=0.74，
136÷200=0.68，345÷500=0.69，564÷800=0.705，701÷
1 000=0.701；
如下表：(2)因为落在钢笔区域的频率为0.701≈0.7，
所以当n很大时，频率将会接近0.7.