七年级数学认识三角形第一课时课件

课件30张PPT。第1课时 1.探究：分别在等腰三角形纸片上折出顶角平分线、底边上的
中线、底边上的高线，观察折痕两旁的部分能否重合？你还发
现了什么？
答：(1)等腰三角形___轴对称图形.
(2)三线合一：等腰三角形顶角的平分线、底边上的中线、底边
上的高重合,它们所在的直线都是等腰三角形的_______.
(3)等腰三角形的两个_____相等.是对称轴底角2.等边三角形是轴对称图形吗?它还有什么性质？
答：___________________________________________________
________________.
3.线段是轴对称图形吗？它有几条对称轴？
答：___________________________________________________
___________________________. 等边三角形是轴对称图形，它有三条对称轴，等边三角形
的三个角都是60° 线段是轴对称图形,它有两条对称轴,一条是线段所在的直
线,一条是线段的垂直平分线【预习思考】
等边三角形与等腰三角形有什么关系？
提示：等边三角形是特殊的等腰三角形，所以等腰三角形包含等边三角形，等边三角形属于等腰三角形，是特殊和一般的关系.
一个角是60°的等腰三角形是等边三角形.
等边一定等腰，等腰不一定等边. 等腰三角形的性质
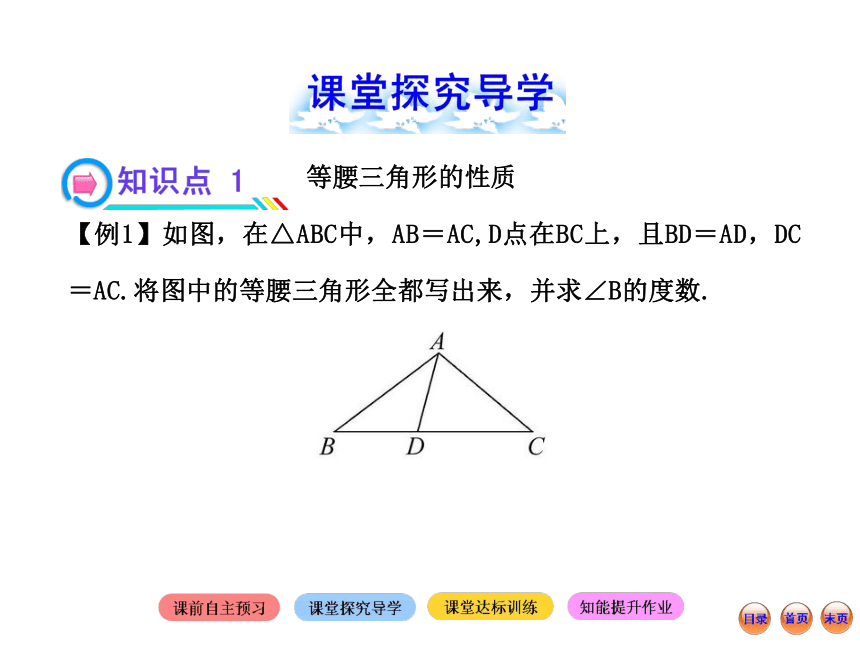
【例1】如图，在△ABC中，AB＝AC,D点在BC上，且BD＝AD，DC＝AC.将图中的等腰三角形全都写出来，并求∠B的度数.【解题探究】(1)图中有几个等腰三角形，判断的理由是什么？
答：有三个等腰三角形，因为AB＝AC，BD＝AD，DC＝AC，由两边相等的三角形是等腰三角形可得△ABC, △ADB, △ACD为等腰三角形.
(2)图中有哪几对角相等？判断的理由是什么？
答：∠B=∠C，∠B=∠BAD，∠DAC=∠ADC，
理由是等腰三角形的两底角相等.(3)∠DAC(∠ADC)与∠B的关系是什么？
答：因为∠ADC=∠B+∠BAD，又因为∠B=∠BAD，所以∠DAC(∠ADC)=2∠B.
(4)在△ABC中你怎样得到∠B的度数？
答：在△ABC中，因为∠B+∠C+∠BAD+∠DAC=180°,所以5∠B=180°，所以∠B=36°.【互动探究】1.等腰三角形中求角的度数问题的一般方法是什么？
提示：等腰三角形中求角的度数，经常应用等腰三角形两底角相等且内角和为180°两个基本定理，由此列方程或进行角的代换，便可得解.
2.等腰三角形中求角的度数需要注意什么问题？
提示：等腰三角形中求角的度数一定要分清已知与要求的角是顶角还是底角，若条件不明确一定要应用分类讨论的思想求解所有可能的结果.【规律总结】
识别等腰三角形的常用方法
(1)寻找三角形是否有两边相等.
(2)寻找三角形是否有两角相等. 【跟踪训练】
1.等腰三角形的对称轴是( )
(A)顶角的平分线 (B)底边上的高
(C)底边上的中线 (D)底边上的高所在的直线
【解析】选D.等腰三角形的对称轴是顶角的平分线、底边上的中线、底边上的高所在的直线.2.等腰三角形两边的长分别为2 cm和5 cm，则这个三角形的周长是( )
(A)9 cm (B)12 cm
(C)9 cm和12 cm (D)在9 cm与12 cm之间
【解析】选B.等腰三角形的腰若是2 cm，则此三边构不成三角形，等腰三角形的腰若是5 cm，则周长为12 cm.3.一个等腰三角形的顶角为50°，则底角为______.
【解析】等腰三角形的两底角相等，又因为等腰三角形的顶角为50°，所以底角为(180°－50°)÷2=65°.
答案：65° 线段的垂直平分线
【例2】(5分)小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗? 请说明理由.【规范解答】同意.如图,设AD与EF相交于点G.
……………………………………………………………………1分
由折叠知, ∠AGE=∠AGF =90° ,EG=FG, ……………………3分
因此AD 垂直平分EF,所以AE=AF,
即△AEF 为等腰三角形. ………………………………………5分【互动探究】线段垂直平分线与等腰三角形的联系是什么？
提示：线段垂直平分线的性质是线段垂直平分线上的点到线段两个端点的距离相等，所以有线段垂直平分线就有等腰三角形的产生，我们在解决问题时可综合利用线段垂直平分线的性质与等腰三角形的性质.【规律总结】
线段的轴对称性
线段是轴对称图形，它可以沿着自身折叠完全重合，即线段自身所在的直线是线段的一条对称轴.这样线段有两条对称轴，一条是线段的垂直平分线，一条是它自身所在的直线.【跟踪训练】
4.在△ABC中，BC=10，BD=8，DE⊥BC，E为BC的中点，则△BCD的周长是( )
(A)26 (B)18 (C)16 (D)28
【解析】选A，因为DE⊥BC，E为BC的中点，所以DE是线段BC的垂直平分线，所以BD=DC=8,所以△BCD的周长为10+8+8=26.5.如图，在△ABC中，分别以点A和点B为圆心，大于 AB的长为
半径画弧，两弧相交于点M,N，作直线MN，交BC于点D，连接AD.
若△ADC的周长为10，AB=7，则△ABC的周长为( )
(A)7 (B)14 (C)17 (D)20【解析】选C.由题意中的作图步骤可知直线MN是线段AB的垂直平分线，所以AD=BD，所以△ABC的周长为AC+CD+BD+AB= AC+CD+AD+AB=10+7=17.6.如图，在△ABC中，AB=AC，D是AB的中点，且DE⊥AB，已知△BCE的周长是8，且AC-BC=2，求AB，BC的长.【解析】∵DE⊥AB,AD=BD,
∴AE=BE,
∴△BCE的周长=BC+CE+BE
=BC+CE+AE=BC+AC=8.
又∵AC-BC=2，
∴AC=5，BC=3，
又∵AB=AC，∴AB=5.1.对于下列判断：(1)关于某一直线成轴对称的两个三角形全等；(2)等腰三角形的对称轴是顶角的平分线；(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点；(4)两个三角形全等，它们关于某直线成轴对称.其中正确的个数为( )
(A)0 (B)1 (C)2 (D)3【解析】选B.(1)关于某一直线成轴对称的两个三角形全等，正确；(2)等腰三角形的对称轴是顶角的平分线所在的直线，故错误；(3)一条线段的两个端点一定是关于经过该线段中点的垂线的对称点，故错误；(4)两个三角形全等，它们不一定成轴对称，故错误.2.等腰三角形有一个内角是40°，则它的一个底角是( )
(A)40° (B)70°
(C)40°或70° (D)70°或70°
【解析】选C.由等腰三角形的两底角相等得若一个底角为40°，则另一个底角也为40°,若顶角为40°,则底角为70°.3.如图，在Rt△ABC中，∠B为直角，DE是AC的垂直平分线，E在BC上，∠BAE∶∠BAC＝1∶5，则∠C＝______.
【解析】因为DE是AC的垂直平分线，所以AE=EC,所以∠C＝∠EAC.又因为∠BAE∶∠BAC＝1∶5，所以设∠BAE=x°,则∠C＝∠EAC=4x°,所以x+4x+4x=90.解得x=10，所以∠C＝40°.
答案：40°4.如图，在△ACD中，AD＝BD＝BC，若∠C＝25°，则∠ADB＝______.

【解析】因为AD＝BD＝BC，所以∠BDC=∠C=25°,∠A=∠ABD=
50°,所以∠ADB＝180°－50°－50°=80°.
答案：80°5.如图,直线MN垂直平分线段AB,CD,垂足分别为点E,F.
试说明：AC=BD，且∠ACD=∠BDC.【解析】因为直线MN垂直平分线段AB,CD,
所以OA=OB,OC=OD,
所以OA+OC=OB+OD,∠OCD=∠ODC,
即AC=BD,∠ACD=∠BDC.