4.2.1等差数列的性质 第2课时 说课课件(共23张PPT)
文档属性
| 名称 | 4.2.1等差数列的性质 第2课时 说课课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-30 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第2课时 等差数列的性质
铜梁二中 数学组
人教A版普通高中教科书数学选择性必修第二册 第四章《数列》 第二单元《等差数列》
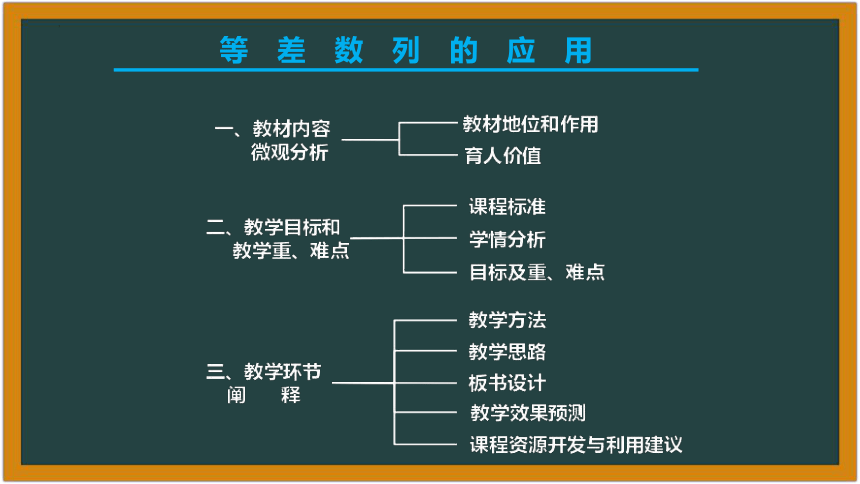
等差数列的应用
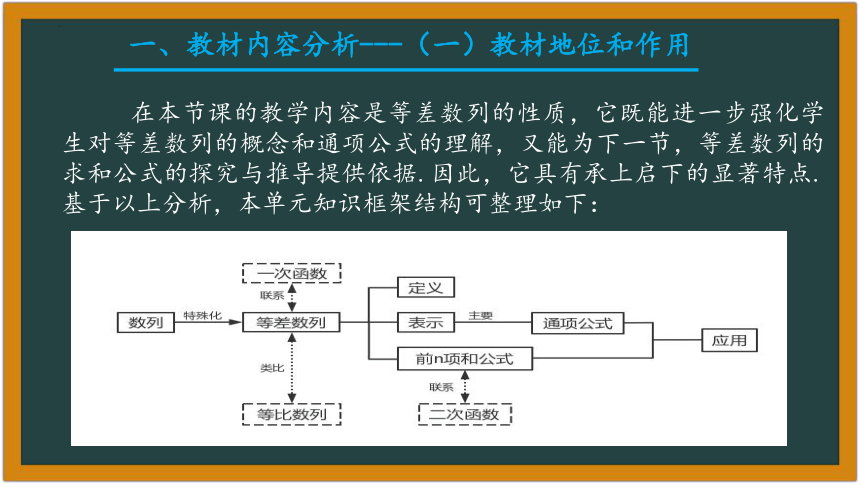
一、教材内容分析---(一)教材地位和作用
在本节课的教学内容是等差数列的性质,它既能进一步强化学生对等差数列的概念和通项公式的理解,又能为下一节,等差数列的求和公式的探究与推导提供依据.因此,它具有承上启下的显著特点.基于以上分析,本单元知识框架结构可整理如下:
一、教材内容分析---(二)育人价值
在探究等差数列性质的过程中,学生会用等差数列的通项公式、方程的思想和基本量的方法来证明等差数列的性质,有助于发展学生推理、运算能力。另外,还从数形结合的角度展示了等差数列的性质,满足了学生的探究欲望,提升学生对数列特殊规律的研究能力.
二、教学目标分析---(一)课程标准
课程目标:
1.掌握等差数列的性质;
2.能在具体的问题情境中,发现数列的等差关系, 并解决相应的问题.
二、教学目标分析---(二)学情分析
数列是一类特殊的函数,而学生在高一时经历了研究函数的一般路径,在知识、经验方面有所积累,并且学生通过前面的学习,对等差数列的概念、通项公式也有了初步的理解,这些都为本课时的应用提供了探究方法和理论基础;在能力水平方面,学生已经具备一定的抽象、推理、类比等能力,但公式的灵活应用能力不足、从实际情境中建立数学模型的能力还有待提升.
二、教学目标分析---(三)教学目标和重、难点
教学目标:
(1)通过观察与联系,能够说明等差数列的下标和项的关系,能够解释等差数列的通项公式与角标性质的内在联系,体会转化与化归的数学思想;
(2)通过数学问题情境,能够从几何角度归纳等差数列下标和项的关系,体会数形结合这一思想方法,发展学生逻辑推理和数学运算素养;
(3)能将实际问题提炼成等差数列模型,识别等差数列的基本量,利用等差数列的通项公式和性质解决问题,进一步体会转化与化归、方程思想,培育学生数学建模素养.
教学重、难点:
教学重点:等差数列通项公式、等差数列的性质.
教学难点:(1)等差数列性质的研究方法;
(2)从实际问题中抽象出等差数列的模型.
二、教学目标分析---(三)教学目标和重、难点
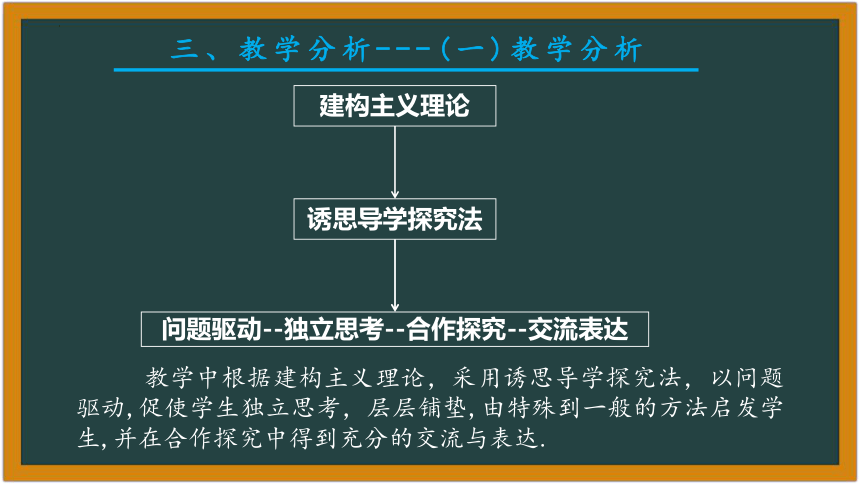
三、教学分析---(一)教学分析
建构主义理论
诱思导学探究法
问题驱动--独立思考--合作探究--交流表达
教学中根据建构主义理论,采用诱思导学探究法,以问题驱动,促使学生独立思考,层层铺垫,由特殊到一般的方法启发学生,并在合作探究中得到充分的交流与表达.
三、教学分析---(二)学法分析
问题情景
知识、技能、核心素养
观察、探究、反思、交流
教学中,让学生在问题情境中,经历知识的形成和发展,通过观察、探索、交流、反思参与学习,认识和理解数学知识,学会学习,提升能力,发展数学核心素养.
三、教学分析---(三)教学思路
设计意图:进一步加深等差数列的概念,引入新的问题,激发学生的学习兴趣.
环节一:新课引入
请同学们思考以下问题:
若等差数列{}为1,3,5,7,…,2n-1,则数列{+2},{2}是等差数列吗?
三、教学分析---(三)教学思路
环节二:回顾旧知
1.等差数列通项公式的变形及推广
(1) =+(-)(∈N*),(2) =+(-)d(,∈N*),
(3)d=(,∈N*,且≠).
2.等差中项
(1)条件:如果,,成等差数列.(2)结论:那么叫做与的等差中项.
(3)满足的关系式是:
设计意图:教师引导学生回顾等差数列通项公式的变形及基本量d的求解公式、等差中项,有利于学生理解公式的变化,认识变化的本质,为学生在后续研究性质的环节中提供有用的工具。
三、教学分析---(三)教学思路
环节三 新知探究
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值会减少d(d为正常数)万元.已知这台设备的使用年限为10年,超过10年 ,它的价值将低于购进价值的5%,设备将报废.请确定d的范围
设计意图:通过生活情境中的数列问题,让学生借助已学的知识完成求解,体会等差数列通项公式的应用价值.
三、教学分析---(三)教学思路
例2 已知等差数列的首项,在中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列.
(1)求数列 的通项公式.
(2) 是不是数列的项?若是,它是 的第几项?若不是 ,请说明理由.
设计意图:通过本例,加深学生对等差数列及其性质的理解和运用.发展学生逻辑推理,直观想象和数学运算的核心素养.
三、教学分析---(三)教学思路
例3 已知数列 是等差数列,,且
(1)求证:
(2) 你能从几何角度解释问题(1)中等差数列的这一性质吗?
设计意图:学生从代数角度、几何角度充分认识了等差数列后,本例恰好从数形结合的角度展示了等差数列的性质,满足了学生的探究欲望,使学生在获得新知的同时,还能够提升其对待特殊数列的特殊规律的研究能力.
三、教学分析---(三)教学思路
环节四 随堂练习
1.在等差数列{}中,已知=10,=-20,则公差等于( )
A.3 B.-6 C.4 D.-3
2.在等差数列{}中,=2, +=10,则等于( )
A.5 B.8 C.10 D.143.
三、教学分析---(三)教学思路
3.在等差数列中,,,则=________.
4.在等差数列中,已知5是和的等差中项,则=________.
5.三个数成等差数列,这三个数的和为6,三个数之积为-24,求这三个数.
设计意图:随堂练习的四个题主要检测学生对本节重点知识和性质的掌握情况,评价采取书面的形式,题目难度适中,各有侧重,既可以引导学生抓住要点,又能够增加学生学习的信心.
三、教学分析---(三)教学思路
环节五 小结提升,形成结构
回顾本节课学习内容,回答下列问题:
(1)等差数列有哪些性质?
(2)推到等差数列的性质的关键是什么?
(3)本节课你学到了哪些数学思想方法?
设计意图:及时巩固,建构等差数列的相关知识,明确数学思想方法,提高认识.
三、教学分析---(三)教学思路
环节六:分层作业,应用迁移
1.基础性作业
(1)必做题:教科书17-18第1、2、4、5题.
(2)选做题:教科书第25页习题4.2第5、10题.
2.拓展性作业
教科书第55页复习参考题4第8(1)题.
设计意图:通过分层作业提供教学的针对性,鼓励不同层次的学生学以致用.
多媒体放映
等差数列的性质
三、教学分析---(四)板书设计
=+(-)(∈N*),
=+(-)d(,∈N*),
d=(,∈N*,且≠).
一、等差数列的通项公式及变形
二、等差数列的性质
若,且
则.
对于本节课,我采用提纲式板书设计。同时通过使用幻灯片辅助板书,节省课堂时间,使课堂进程更加连贯.具体如下:
(1)通过具体问题探究,经历从特殊到一般的学习过程,能够理解等差数列的通项公式和性质,会用等差数列通项公式、基本量的方法和等差数列的性质求解等差数列的有关问题,发展学生逻辑推理、数学运算等核心素养.
(2)深刻体会将实际问题转化为数学问题,并用相应的数学知识解决问题,体会数学应用的广泛性,发展学生数学抽象素养.
三、教学分析---(五)教学效果预测
(1)注重培养学生的自主学习习惯
教师可在课前为学生准备导学案,使学生带着问题进行自主预习,逐步形成能学习、会学习、善学习的优良态势;
(2)注重联系,突出转化,强化对等差数列的整体认识
本单元以概念和公式为主,因此,在教学设计时不仅要注重概念公式的形成过程,更要注重公式之间的联系,注重公式与函数之间的联系,强化对等差数列的整体认识,体会数学的整体性.
三、教学分析---(六)课程资源开发与利用建议
(3)注重培育学生数学学科素养
每一个堂课都是发展学生核心素养的好契机。无论是由现实问题转化为数学问题、从特殊到一般,或者是归纳小结形成知识框架等,都能发展学生数学抽象素养、逻辑推理、数学建模等核心素养;数学上大多数应用课都与运算有关,因此教科书设置了例题、练习和习题,教学时应引导学生注重依据定义、性质和进行求解,发展学生数学运算素养;
以上就是我对《等差数列的性质》这一节的认识和构想,不当之处,恳请各位专家批评指正。谢谢!
三、教学分析---(六)课程资源开发与利用建议
第2课时 等差数列的性质
铜梁二中 数学组
人教A版普通高中教科书数学选择性必修第二册 第四章《数列》 第二单元《等差数列》
等差数列的应用
一、教材内容分析---(一)教材地位和作用
在本节课的教学内容是等差数列的性质,它既能进一步强化学生对等差数列的概念和通项公式的理解,又能为下一节,等差数列的求和公式的探究与推导提供依据.因此,它具有承上启下的显著特点.基于以上分析,本单元知识框架结构可整理如下:
一、教材内容分析---(二)育人价值
在探究等差数列性质的过程中,学生会用等差数列的通项公式、方程的思想和基本量的方法来证明等差数列的性质,有助于发展学生推理、运算能力。另外,还从数形结合的角度展示了等差数列的性质,满足了学生的探究欲望,提升学生对数列特殊规律的研究能力.
二、教学目标分析---(一)课程标准
课程目标:
1.掌握等差数列的性质;
2.能在具体的问题情境中,发现数列的等差关系, 并解决相应的问题.
二、教学目标分析---(二)学情分析
数列是一类特殊的函数,而学生在高一时经历了研究函数的一般路径,在知识、经验方面有所积累,并且学生通过前面的学习,对等差数列的概念、通项公式也有了初步的理解,这些都为本课时的应用提供了探究方法和理论基础;在能力水平方面,学生已经具备一定的抽象、推理、类比等能力,但公式的灵活应用能力不足、从实际情境中建立数学模型的能力还有待提升.
二、教学目标分析---(三)教学目标和重、难点
教学目标:
(1)通过观察与联系,能够说明等差数列的下标和项的关系,能够解释等差数列的通项公式与角标性质的内在联系,体会转化与化归的数学思想;
(2)通过数学问题情境,能够从几何角度归纳等差数列下标和项的关系,体会数形结合这一思想方法,发展学生逻辑推理和数学运算素养;
(3)能将实际问题提炼成等差数列模型,识别等差数列的基本量,利用等差数列的通项公式和性质解决问题,进一步体会转化与化归、方程思想,培育学生数学建模素养.
教学重、难点:
教学重点:等差数列通项公式、等差数列的性质.
教学难点:(1)等差数列性质的研究方法;
(2)从实际问题中抽象出等差数列的模型.
二、教学目标分析---(三)教学目标和重、难点
三、教学分析---(一)教学分析
建构主义理论
诱思导学探究法
问题驱动--独立思考--合作探究--交流表达
教学中根据建构主义理论,采用诱思导学探究法,以问题驱动,促使学生独立思考,层层铺垫,由特殊到一般的方法启发学生,并在合作探究中得到充分的交流与表达.
三、教学分析---(二)学法分析
问题情景
知识、技能、核心素养
观察、探究、反思、交流
教学中,让学生在问题情境中,经历知识的形成和发展,通过观察、探索、交流、反思参与学习,认识和理解数学知识,学会学习,提升能力,发展数学核心素养.
三、教学分析---(三)教学思路
设计意图:进一步加深等差数列的概念,引入新的问题,激发学生的学习兴趣.
环节一:新课引入
请同学们思考以下问题:
若等差数列{}为1,3,5,7,…,2n-1,则数列{+2},{2}是等差数列吗?
三、教学分析---(三)教学思路
环节二:回顾旧知
1.等差数列通项公式的变形及推广
(1) =+(-)(∈N*),(2) =+(-)d(,∈N*),
(3)d=(,∈N*,且≠).
2.等差中项
(1)条件:如果,,成等差数列.(2)结论:那么叫做与的等差中项.
(3)满足的关系式是:
设计意图:教师引导学生回顾等差数列通项公式的变形及基本量d的求解公式、等差中项,有利于学生理解公式的变化,认识变化的本质,为学生在后续研究性质的环节中提供有用的工具。
三、教学分析---(三)教学思路
环节三 新知探究
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值会减少d(d为正常数)万元.已知这台设备的使用年限为10年,超过10年 ,它的价值将低于购进价值的5%,设备将报废.请确定d的范围
设计意图:通过生活情境中的数列问题,让学生借助已学的知识完成求解,体会等差数列通项公式的应用价值.
三、教学分析---(三)教学思路
例2 已知等差数列的首项,在中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列.
(1)求数列 的通项公式.
(2) 是不是数列的项?若是,它是 的第几项?若不是 ,请说明理由.
设计意图:通过本例,加深学生对等差数列及其性质的理解和运用.发展学生逻辑推理,直观想象和数学运算的核心素养.
三、教学分析---(三)教学思路
例3 已知数列 是等差数列,,且
(1)求证:
(2) 你能从几何角度解释问题(1)中等差数列的这一性质吗?
设计意图:学生从代数角度、几何角度充分认识了等差数列后,本例恰好从数形结合的角度展示了等差数列的性质,满足了学生的探究欲望,使学生在获得新知的同时,还能够提升其对待特殊数列的特殊规律的研究能力.
三、教学分析---(三)教学思路
环节四 随堂练习
1.在等差数列{}中,已知=10,=-20,则公差等于( )
A.3 B.-6 C.4 D.-3
2.在等差数列{}中,=2, +=10,则等于( )
A.5 B.8 C.10 D.143.
三、教学分析---(三)教学思路
3.在等差数列中,,,则=________.
4.在等差数列中,已知5是和的等差中项,则=________.
5.三个数成等差数列,这三个数的和为6,三个数之积为-24,求这三个数.
设计意图:随堂练习的四个题主要检测学生对本节重点知识和性质的掌握情况,评价采取书面的形式,题目难度适中,各有侧重,既可以引导学生抓住要点,又能够增加学生学习的信心.
三、教学分析---(三)教学思路
环节五 小结提升,形成结构
回顾本节课学习内容,回答下列问题:
(1)等差数列有哪些性质?
(2)推到等差数列的性质的关键是什么?
(3)本节课你学到了哪些数学思想方法?
设计意图:及时巩固,建构等差数列的相关知识,明确数学思想方法,提高认识.
三、教学分析---(三)教学思路
环节六:分层作业,应用迁移
1.基础性作业
(1)必做题:教科书17-18第1、2、4、5题.
(2)选做题:教科书第25页习题4.2第5、10题.
2.拓展性作业
教科书第55页复习参考题4第8(1)题.
设计意图:通过分层作业提供教学的针对性,鼓励不同层次的学生学以致用.
多媒体放映
等差数列的性质
三、教学分析---(四)板书设计
=+(-)(∈N*),
=+(-)d(,∈N*),
d=(,∈N*,且≠).
一、等差数列的通项公式及变形
二、等差数列的性质
若,且
则.
对于本节课,我采用提纲式板书设计。同时通过使用幻灯片辅助板书,节省课堂时间,使课堂进程更加连贯.具体如下:
(1)通过具体问题探究,经历从特殊到一般的学习过程,能够理解等差数列的通项公式和性质,会用等差数列通项公式、基本量的方法和等差数列的性质求解等差数列的有关问题,发展学生逻辑推理、数学运算等核心素养.
(2)深刻体会将实际问题转化为数学问题,并用相应的数学知识解决问题,体会数学应用的广泛性,发展学生数学抽象素养.
三、教学分析---(五)教学效果预测
(1)注重培养学生的自主学习习惯
教师可在课前为学生准备导学案,使学生带着问题进行自主预习,逐步形成能学习、会学习、善学习的优良态势;
(2)注重联系,突出转化,强化对等差数列的整体认识
本单元以概念和公式为主,因此,在教学设计时不仅要注重概念公式的形成过程,更要注重公式之间的联系,注重公式与函数之间的联系,强化对等差数列的整体认识,体会数学的整体性.
三、教学分析---(六)课程资源开发与利用建议
(3)注重培育学生数学学科素养
每一个堂课都是发展学生核心素养的好契机。无论是由现实问题转化为数学问题、从特殊到一般,或者是归纳小结形成知识框架等,都能发展学生数学抽象素养、逻辑推理、数学建模等核心素养;数学上大多数应用课都与运算有关,因此教科书设置了例题、练习和习题,教学时应引导学生注重依据定义、性质和进行求解,发展学生数学运算素养;
以上就是我对《等差数列的性质》这一节的认识和构想,不当之处,恳请各位专家批评指正。谢谢!
三、教学分析---(六)课程资源开发与利用建议
