几何证明之命题、公理和定理[上学期]
图片预览





文档简介
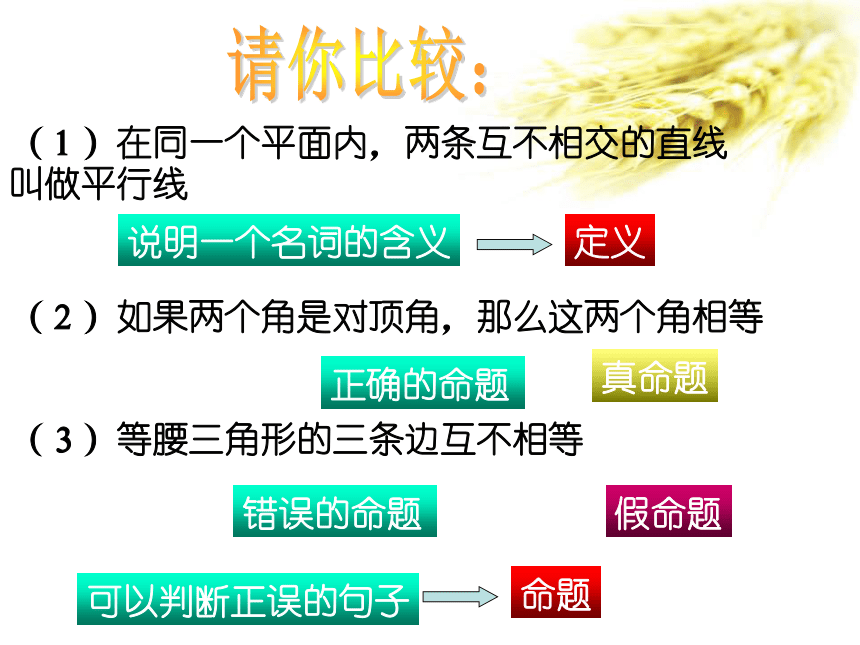
课件18张PPT。命题 定理 公理请你比较:(1)在同一个平面内,两条互不相交的直线叫做平行线(2)如果两个角是对顶角,那么这两个角相等(3)等腰三角形的三条边互不相等说明一个名词的含义定义可以判断正误的句子命题真命题假命题错误的命题正确的命题判断下列语句是否是命题(1)三角形的一个外角大于任何一个与之不相邻的内角(2)画一条直线(3)有两条边相等的三角形是等腰三角形(4)对顶角相等命题判断一个句子是否是命题,关键在于:命题通常都是陈述句,是可以表达对事物有所肯定或否定的语句我是中学生是命题今天可能下雨不是命题今天天气真好啊!不是命题对顶角相等吗?不是命题判断下列命题哪些是真命题,哪些是假命题?1. 面积相等的两个三角形全等2. 两个全等三角形的面积相等3. 任何一条线段有且只有一条垂直平分线 4.如果a>b,b>c,那么a=c;5.两角和其中一角的对边对应相等的两个三角形全等;正确的命题即真命题用逻辑推理来判定其正确,
假命题通过举反例的方法证明其错误请你写出与平行四边形有关的真命题请你写出两个与圆有关的真命题观察下列命题:这些命题有什么共同的结构待征?1、如果两个三角形的三条边对应相等,
那么这两个三角形全等;
2、如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等;3、如果在一个三角形中,有两个角相等,
那么这两个角所对的边也相等数学中的命题1、如果两个三角形的三条边对应相等,那么这三角形全等;题设结论已知事项由已知事项推断
出来的事项命题都可以写成“如果……那么……”的形式;其中“如果”引出的部分是题设,“那么”引出的部分是结论。数学中的命题数学中的命题题设结论已知事项由已知事项推出的事项如果……那么……如果两个角是对顶角,那么这两个角相等eg:题设结论有两条边相等的三角形是等腰三角形如果在一个三角形中,有两条边相等,那么这个三角形是等腰三角形数学中的命题请你说出下列命题的题设和结论3. 如果∠1 = ∠2,∠2 = ∠3,那么∠1 = ∠31. 如果两条直线相交,那么它们只有一个交点。2. 两条直线被第三条直线所截,
如果同旁内角互补,
那么这两条直线平行。两条直线相交只有一个交点同旁内角互补这两条直线平行∠1 = ∠2,∠2 = ∠3∠1 = ∠3两条直线被第三条直线所截,请你试试将下列命题改写成如果……那么……的形式(1)等角的补角相等(2)平分弦的直径垂直于弦并且平分这条弦所对的弧(3)在同一平面内,两条直线不平行,它们一定相交如果两个角分别是两个相等的角的补角那么这两个角相等如果一条直径平分弦那么这条直径垂直于弦并且平分这条弦所对的弧在同一平面内,如果两条直线不平行那么这两条直线一定相交练习:有一个内角为60度的等腰三角形是等边三角形 将下列命题改写成如果……那么……的形式邻补角的平分线互相垂直直角都相等 等边对等角 如何证实一个命题是真命题呢用我们以前学过的观察,实验,验证特例等方法.这些方法往往并不可靠.能不能根据已经知道的真命题证实呢?那已经知道的真命题又是如何证实的?.哦……那可怎么办想一想古希腊数学家欧几里得(Euclid,公元前300前后).公理:经过人们长期时间总结得到,并作为判断其它命题真假的原始依据的命题叫做公理
证明:根据题设、定义以及已经被确认的公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明定理:从公理或其它真命题出发,用逻辑推理的方法判断它们是正确的,并且本身可以进一步作为判断其它命题真假的依据的真命题
读一读书 P58<<几何原本>>(1)经过两点有一条直线,并且只有一条直线(2)在所有连结两点的线中,线段最短(3)经过已知直线外的一点,有一条直线而且只有一条直线与已知直线平行通过实际操作:直线的基本性质线段的基本性质平行公理真命题公理(4)两条平行线被第三条直线所截,同位角相等平行的判定公理在所有连结两点的线中,线段最短三角形的任何两边的和大于第三边公理定理书P98-P101参考:小结:1、几何原本的作者和译者
2、命题的概念及能分清命题的题设和结论部分
3、命题的真假判定1 、 A册/22.2
2、一课一练 P73-P74
3、同步 P93-94
4、国庆作业作业
假命题通过举反例的方法证明其错误请你写出与平行四边形有关的真命题请你写出两个与圆有关的真命题观察下列命题:这些命题有什么共同的结构待征?1、如果两个三角形的三条边对应相等,
那么这两个三角形全等;
2、如果一个三角形是等腰三角形,
那么这个三角形的两个底角相等;3、如果在一个三角形中,有两个角相等,
那么这两个角所对的边也相等数学中的命题1、如果两个三角形的三条边对应相等,那么这三角形全等;题设结论已知事项由已知事项推断
出来的事项命题都可以写成“如果……那么……”的形式;其中“如果”引出的部分是题设,“那么”引出的部分是结论。数学中的命题数学中的命题题设结论已知事项由已知事项推出的事项如果……那么……如果两个角是对顶角,那么这两个角相等eg:题设结论有两条边相等的三角形是等腰三角形如果在一个三角形中,有两条边相等,那么这个三角形是等腰三角形数学中的命题请你说出下列命题的题设和结论3. 如果∠1 = ∠2,∠2 = ∠3,那么∠1 = ∠31. 如果两条直线相交,那么它们只有一个交点。2. 两条直线被第三条直线所截,
如果同旁内角互补,
那么这两条直线平行。两条直线相交只有一个交点同旁内角互补这两条直线平行∠1 = ∠2,∠2 = ∠3∠1 = ∠3两条直线被第三条直线所截,请你试试将下列命题改写成如果……那么……的形式(1)等角的补角相等(2)平分弦的直径垂直于弦并且平分这条弦所对的弧(3)在同一平面内,两条直线不平行,它们一定相交如果两个角分别是两个相等的角的补角那么这两个角相等如果一条直径平分弦那么这条直径垂直于弦并且平分这条弦所对的弧在同一平面内,如果两条直线不平行那么这两条直线一定相交练习:有一个内角为60度的等腰三角形是等边三角形 将下列命题改写成如果……那么……的形式邻补角的平分线互相垂直直角都相等 等边对等角 如何证实一个命题是真命题呢用我们以前学过的观察,实验,验证特例等方法.这些方法往往并不可靠.能不能根据已经知道的真命题证实呢?那已经知道的真命题又是如何证实的?.哦……那可怎么办想一想古希腊数学家欧几里得(Euclid,公元前300前后).公理:经过人们长期时间总结得到,并作为判断其它命题真假的原始依据的命题叫做公理
证明:根据题设、定义以及已经被确认的公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明定理:从公理或其它真命题出发,用逻辑推理的方法判断它们是正确的,并且本身可以进一步作为判断其它命题真假的依据的真命题
读一读书 P58<<几何原本>>(1)经过两点有一条直线,并且只有一条直线(2)在所有连结两点的线中,线段最短(3)经过已知直线外的一点,有一条直线而且只有一条直线与已知直线平行通过实际操作:直线的基本性质线段的基本性质平行公理真命题公理(4)两条平行线被第三条直线所截,同位角相等平行的判定公理在所有连结两点的线中,线段最短三角形的任何两边的和大于第三边公理定理书P98-P101参考:小结:1、几何原本的作者和译者
2、命题的概念及能分清命题的题设和结论部分
3、命题的真假判定1 、 A册/22.2
2、一课一练 P73-P74
3、同步 P93-94
4、国庆作业作业
