证明的步骤[上学期]
图片预览





文档简介
课件31张PPT。 22.3
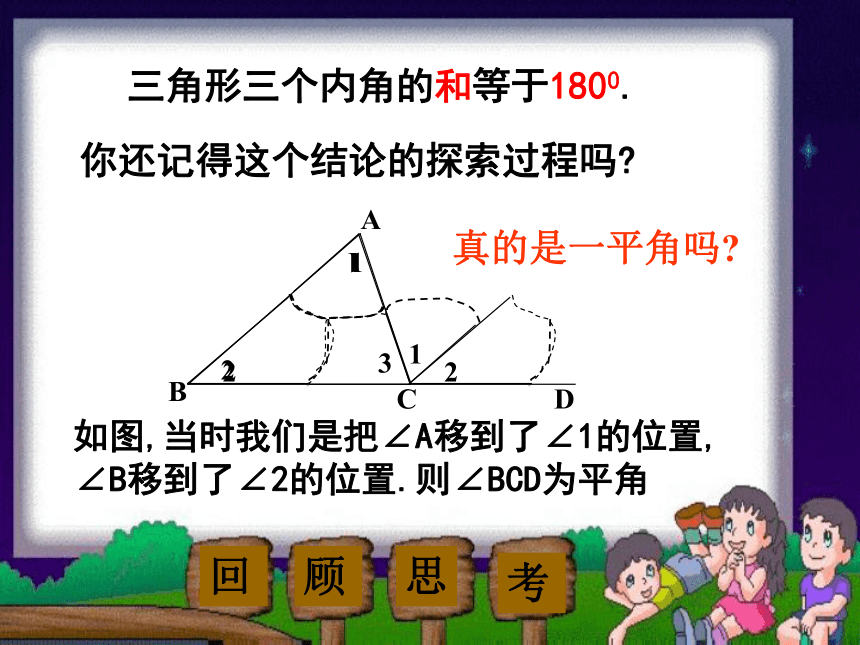
证明de步骤三角形三个内角的和等于1800.如图,当时我们是把∠A移到了∠1的位置,
∠B移到了∠2的位置.则∠BCD为平角你还记得这个结论的探索过程吗?真的是一平角吗?回顾思考12ABD3C 如果不能撕下来,
如:在黑板上怎么办?通过观察仅能提出一个猜想,
这个猜想可能成立,也可能不成立,
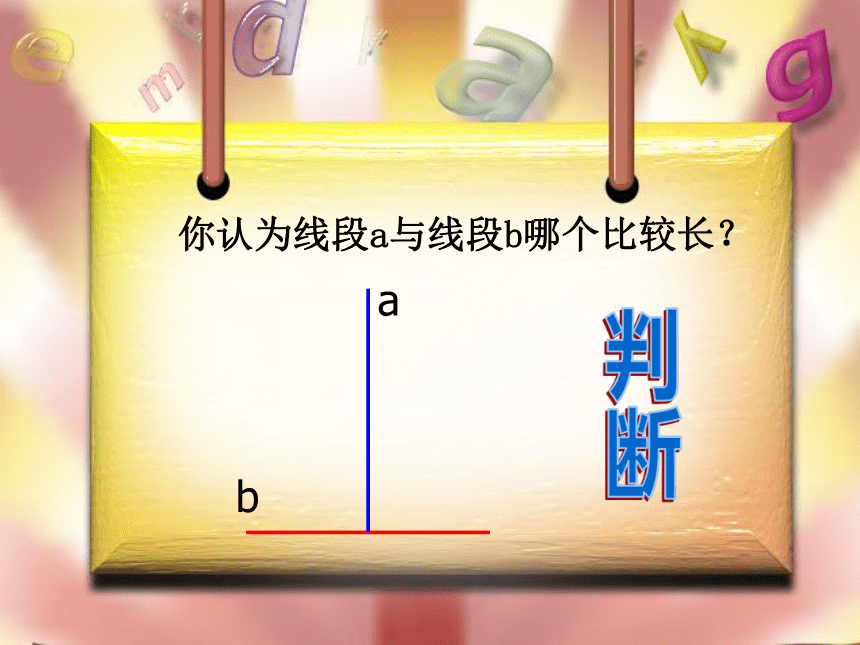
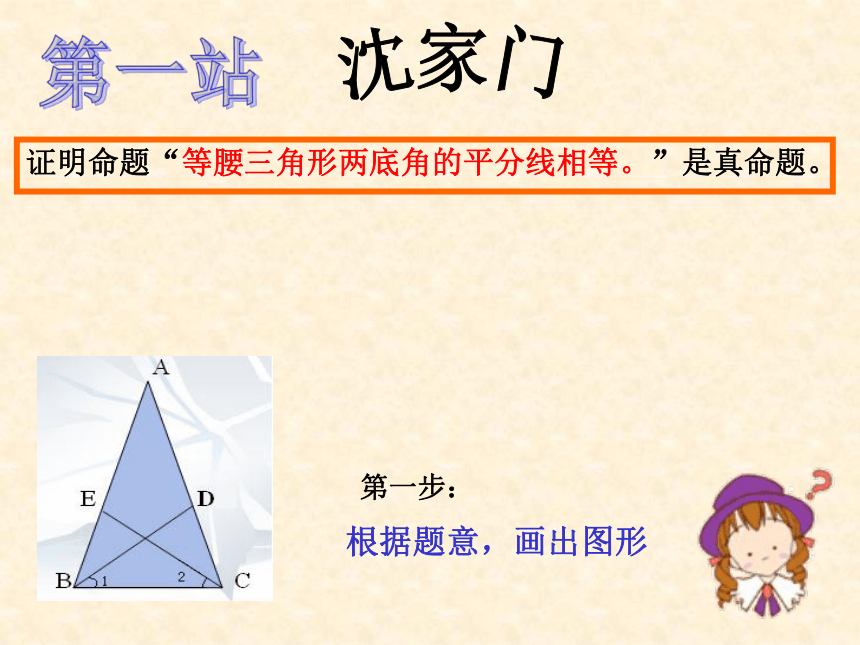
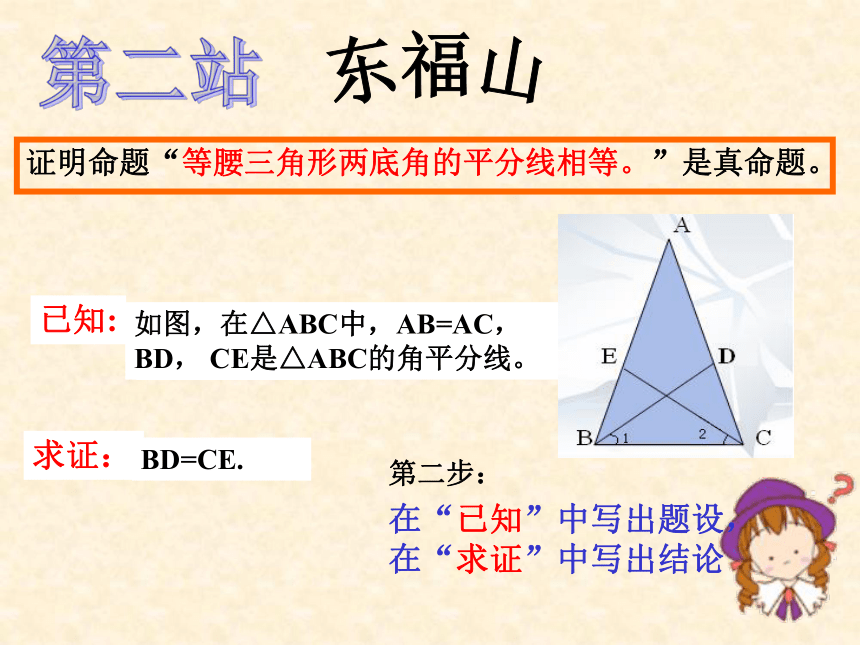
对它的正确性还要进行证实。b 你认为线段a与线段b哪个比较长?判断如何判断一个命题是真命题?二、列举举不胜举!一、目测(直观)错觉!当n=6时, n2-3n+7 =25=55(不是质数)三、测量存在误差! 当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是质数.那么,命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗?四、猜测 假如用一根比地球赤道长1米的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大(把地球看成球形)?能放进一颗红枣吗?能放进一个拳头吗? (设C表示赤道周长)不可靠!新课讲解: 要判定一个命题是真命题,往往需要根据题设、定义以及被确认的公理、定理等,来判定一个命题是否正确,这样的推理过程叫做 证明 。说明了证明的必要性!既然证明那么重要,那我们如何证明呢?“证明”之旅沈家门第一站第二站第三站东福山庙子湖证明命题“等腰三角形两底角的平分线相等。”是真命题。有纪念品等你拿哦!沈家门第一站第一步:根据题意,画出图形证明命题“等腰三角形两底角的平分线相等。”是真命题。东福山第二站第二步:题设:等腰三角形两底角的平分线结论:在“已知”中写出题设,在“求证”中写出结论求证:证明命题“等腰三角形两底角的平分线相等。”是真命题。已知:如图,在△ABC中,AB=AC,
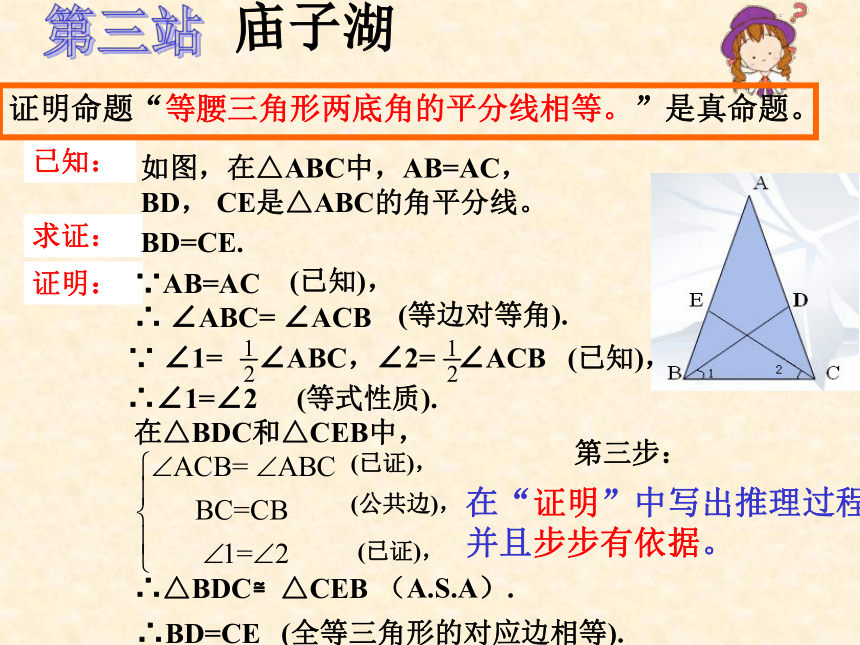
BD, CE是△ABC的角平分线。相等BD=CE.庙子湖第三站第三步:在“证明”中写出推理过程,并且步步有依据。已知:求证:证明:证明命题“等腰三角形两底角的平分线相等。”是真命题。如图,在△ABC中,AB=AC,
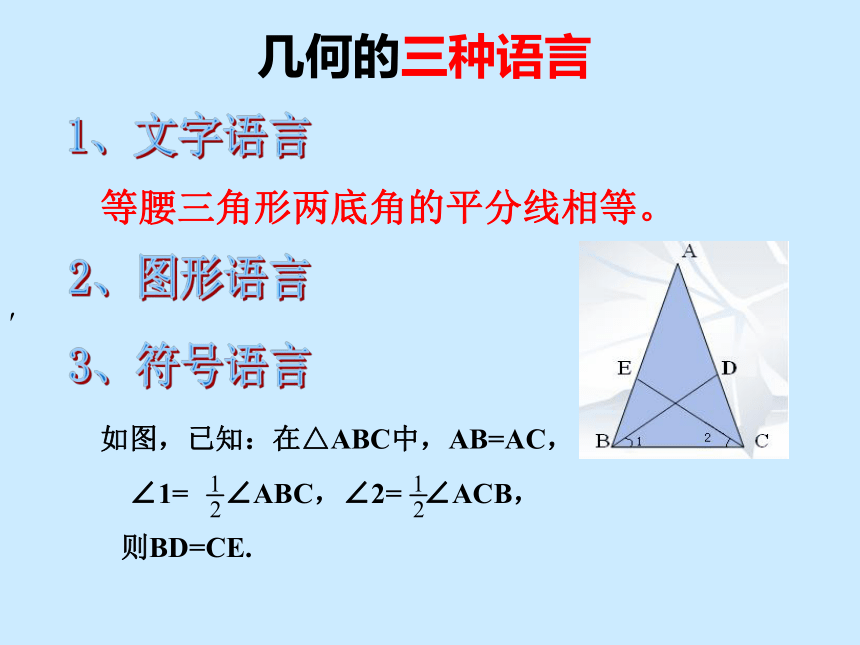
BD, CE是△ABC的角平分线。BD=CE.∵AB=AC∵ ∠1= ∠ABC,∠2= ∠ACB∴△BDC≌△CEB∴ ∠ABC= ∠ACB(等边对等角).(已知),(已知),∴∠1=∠2(等式性质).在△BDC和△CEB中,(已证),(公共边),(已证),∴BD=CE(A.S.A).(全等三角形的对应边相等).几何的三种语言′等腰三角形两底角的平分线相等。1、文字语言2、图形语言3、符号语言如图,已知:在△ABC中,AB=AC, ∠1= ∠ABC,∠2= ∠ACB,则BD=CE.经过刚才三站的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?说一说(1)根据题意,作出图形并在图
上标出必要的字母或符号。(2)根据题设和结论,结合图
形,写出“已知”和“求证”。(3)通过分析,写出证明过程。 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行;
2)内错角相等,两直线平行;
3)一个角的平分线上的点到这个角的两边
的距离相等;
4)两条平行线的一对内错角的平分线互相
平行. 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行; 已知:b⊥a , c⊥aabc 求证:b∥c 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
2)内错角相等,两直线平行; 已知:如图,直线a、b被直线 c所截,
且∠1=∠2 求证:a∥babc21 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
3)一个角的平分线上的点到这个角的两边
的距离相等;已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
4)两条平行线的一对内错角的平分线互相
平行.已知:如图,AB、CD被直线EF所截,且
AB∥CD,EG、FH分别是∠AEF和
∠EFD的平分线
求证:EG∥FH练一练请按照几何命题证明的步骤,证明命题“线段的垂直平分线上的点和这条线段的两个端点的距离相等”是真命题。新课讲解: 在证明的过程中,由于证明的需要,可以在原来的图形上添画一些线,像这样的线叫做辅助线。辅助线通常画成虚线!证明:延长AD至E
∵∠BDE=∠B+∠3 ∠ CDE=∠C+∠4
(三角形的一个外角等于和它不相邻的两个内角的和),
又 ∵ ∠ BDC =∠BDE +∠ CDE (已知),
∴ ∠ BDC = ∠B+∠C+∠3+∠4(等量代换).
又 ∵ ∠BAC = ∠3+∠4(已知),
∴ ∠ BDC = ∠B+∠C+ ∠BAC (等量代换).例1、 如图,已知AD是△ABD
和△ACD的公共边.求证:
∠BDC=∠BAC+∠B+∠CE一个量用与它相等的量去代替叫做等量代换。例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.ABDFCEG⌒例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.ABDFCEH⌒2例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
求证:AB=AC+CDE例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
求证:AB=AC+CDF例4.如图,已知AB=AE,BC=DE,
∠B= ∠E,AF⊥CD于F.
求证:CF=DF.ABCDEF新课讲解:如何判断一个命题是假命题? 只要举出一个例子(反例),
它符合命题的题设,但不满足
结论就可以了.判断下列命题是真命题还是假命题.
如果是假命题,举出一个反例:1)相等的角是对顶角;
2)同位角相等;
3)邻补角是互补的角;
4)互补的角是邻补角;
5)如果一个数能被2整除,那么这个数
也能被4整除;判断下列命题是真命题还是假命题.
如果是假命题,举出一个反例:6)不等式的两边都乘以同一个数,不
等号的方向不变;
7)在平面内,经过一点有且只有一条
直线与已知直线垂直;
8)两个锐角的和是锐角.小结:定 理 与 证 明1.命题证明的
一般步骤2.命题的证明3.判断假命题的方法:(1)画图;
(2)写已知、求证;
(3)写推理过程.举反例回家作业1、A册/22.3
2、同步22.3
3、一课一练22.3再见SEE YOU !
证明de步骤三角形三个内角的和等于1800.如图,当时我们是把∠A移到了∠1的位置,
∠B移到了∠2的位置.则∠BCD为平角你还记得这个结论的探索过程吗?真的是一平角吗?回顾思考12ABD3C 如果不能撕下来,
如:在黑板上怎么办?通过观察仅能提出一个猜想,
这个猜想可能成立,也可能不成立,
对它的正确性还要进行证实。b 你认为线段a与线段b哪个比较长?判断如何判断一个命题是真命题?二、列举举不胜举!一、目测(直观)错觉!当n=6时, n2-3n+7 =25=55(不是质数)三、测量存在误差! 当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是质数.那么,命题“对于自然数n,代数式n2-3n+7的值都是质数”是真命题吗?四、猜测 假如用一根比地球赤道长1米的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大(把地球看成球形)?能放进一颗红枣吗?能放进一个拳头吗? (设C表示赤道周长)不可靠!新课讲解: 要判定一个命题是真命题,往往需要根据题设、定义以及被确认的公理、定理等,来判定一个命题是否正确,这样的推理过程叫做 证明 。说明了证明的必要性!既然证明那么重要,那我们如何证明呢?“证明”之旅沈家门第一站第二站第三站东福山庙子湖证明命题“等腰三角形两底角的平分线相等。”是真命题。有纪念品等你拿哦!沈家门第一站第一步:根据题意,画出图形证明命题“等腰三角形两底角的平分线相等。”是真命题。东福山第二站第二步:题设:等腰三角形两底角的平分线结论:在“已知”中写出题设,在“求证”中写出结论求证:证明命题“等腰三角形两底角的平分线相等。”是真命题。已知:如图,在△ABC中,AB=AC,
BD, CE是△ABC的角平分线。相等BD=CE.庙子湖第三站第三步:在“证明”中写出推理过程,并且步步有依据。已知:求证:证明:证明命题“等腰三角形两底角的平分线相等。”是真命题。如图,在△ABC中,AB=AC,
BD, CE是△ABC的角平分线。BD=CE.∵AB=AC∵ ∠1= ∠ABC,∠2= ∠ACB∴△BDC≌△CEB∴ ∠ABC= ∠ACB(等边对等角).(已知),(已知),∴∠1=∠2(等式性质).在△BDC和△CEB中,(已证),(公共边),(已证),∴BD=CE(A.S.A).(全等三角形的对应边相等).几何的三种语言′等腰三角形两底角的平分线相等。1、文字语言2、图形语言3、符号语言如图,已知:在△ABC中,AB=AC, ∠1= ∠ABC,∠2= ∠ACB,则BD=CE.经过刚才三站的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?说一说(1)根据题意,作出图形并在图
上标出必要的字母或符号。(2)根据题设和结论,结合图
形,写出“已知”和“求证”。(3)通过分析,写出证明过程。 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行;
2)内错角相等,两直线平行;
3)一个角的平分线上的点到这个角的两边
的距离相等;
4)两条平行线的一对内错角的平分线互相
平行. 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行; 已知:b⊥a , c⊥aabc 求证:b∥c 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
2)内错角相等,两直线平行; 已知:如图,直线a、b被直线 c所截,
且∠1=∠2 求证:a∥babc21 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
3)一个角的平分线上的点到这个角的两边
的距离相等;已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
4)两条平行线的一对内错角的平分线互相
平行.已知:如图,AB、CD被直线EF所截,且
AB∥CD,EG、FH分别是∠AEF和
∠EFD的平分线
求证:EG∥FH练一练请按照几何命题证明的步骤,证明命题“线段的垂直平分线上的点和这条线段的两个端点的距离相等”是真命题。新课讲解: 在证明的过程中,由于证明的需要,可以在原来的图形上添画一些线,像这样的线叫做辅助线。辅助线通常画成虚线!证明:延长AD至E
∵∠BDE=∠B+∠3 ∠ CDE=∠C+∠4
(三角形的一个外角等于和它不相邻的两个内角的和),
又 ∵ ∠ BDC =∠BDE +∠ CDE (已知),
∴ ∠ BDC = ∠B+∠C+∠3+∠4(等量代换).
又 ∵ ∠BAC = ∠3+∠4(已知),
∴ ∠ BDC = ∠B+∠C+ ∠BAC (等量代换).例1、 如图,已知AD是△ABD
和△ACD的公共边.求证:
∠BDC=∠BAC+∠B+∠CE一个量用与它相等的量去代替叫做等量代换。例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.ABDFCEG⌒例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.ABDFCEH⌒2例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
求证:AB=AC+CDE例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
求证:AB=AC+CDF例4.如图,已知AB=AE,BC=DE,
∠B= ∠E,AF⊥CD于F.
求证:CF=DF.ABCDEF新课讲解:如何判断一个命题是假命题? 只要举出一个例子(反例),
它符合命题的题设,但不满足
结论就可以了.判断下列命题是真命题还是假命题.
如果是假命题,举出一个反例:1)相等的角是对顶角;
2)同位角相等;
3)邻补角是互补的角;
4)互补的角是邻补角;
5)如果一个数能被2整除,那么这个数
也能被4整除;判断下列命题是真命题还是假命题.
如果是假命题,举出一个反例:6)不等式的两边都乘以同一个数,不
等号的方向不变;
7)在平面内,经过一点有且只有一条
直线与已知直线垂直;
8)两个锐角的和是锐角.小结:定 理 与 证 明1.命题证明的
一般步骤2.命题的证明3.判断假命题的方法:(1)画图;
(2)写已知、求证;
(3)写推理过程.举反例回家作业1、A册/22.3
2、同步22.3
3、一课一练22.3再见SEE YOU !
