证明举例6[上学期]
图片预览



文档简介
课件17张PPT。2006.10.24 17.2证明举例(6)温故知新请大家回顾等腰三角形具有哪些性质?
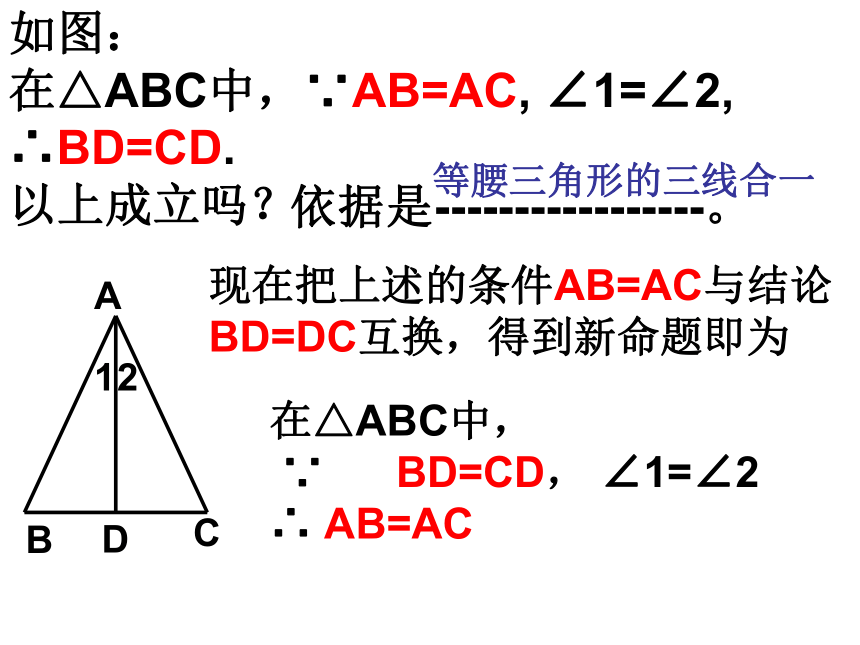
在△ABC中,∵AB=AC, ∠1=∠2, ∴BD=CD.
以上成立吗?在△ABC中,
∵ BD=CD, ∠1=∠2
∴ AB=AC 等腰三角形的三线合一如图:现在把上述的条件AB=AC与结论BD=DC互换,得到新命题即为
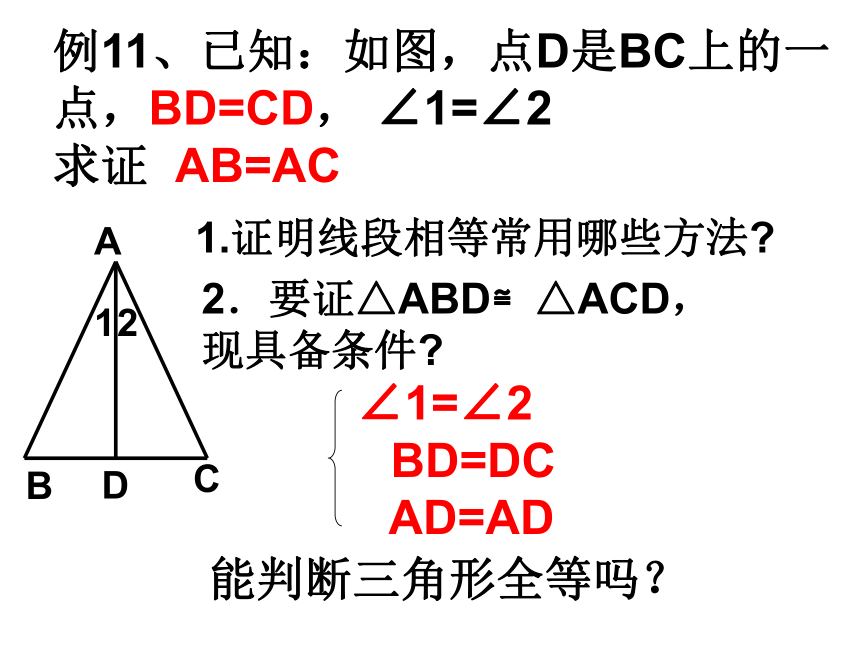
依据是-----------------。例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC 1.证明线段相等常用哪些方法?2.要证△ABD≌△ACD,
现具备条件? ∠1=∠2
BD=DC
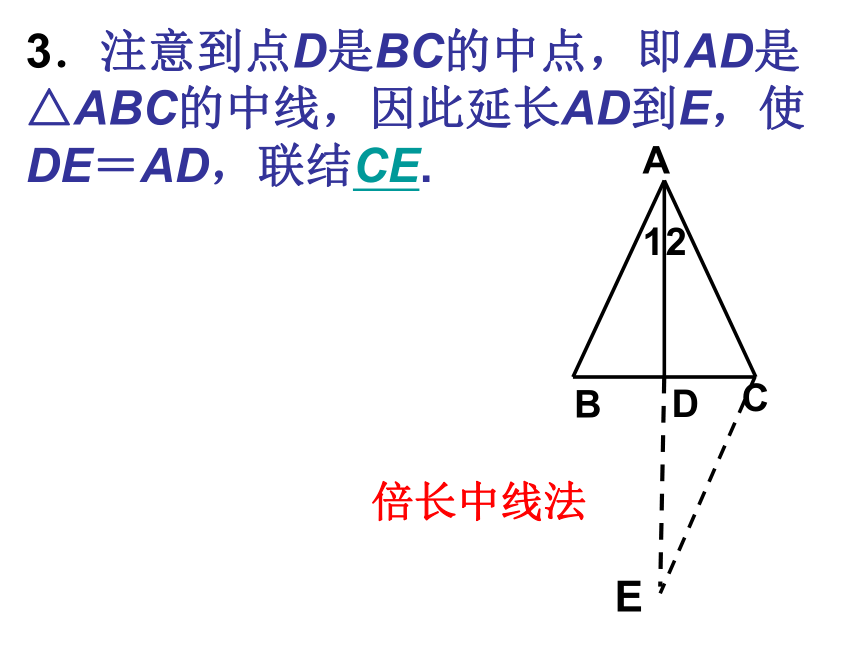
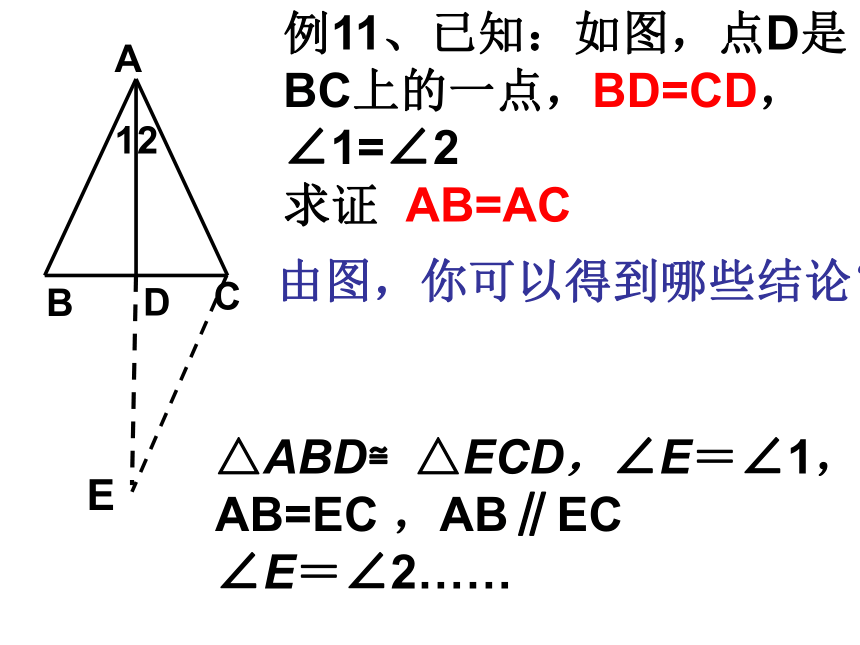
AD=AD能判断三角形全等吗?3.注意到点D是BC的中点,即AD是 △ABC的中线,因此延长AD到E,使DE=AD,联结CE.倍长中线法E例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC由图,你可以得到哪些结论?△ABD≌△ECD,∠E=∠1,
AB=EC ,AB∥EC
∠E=∠2……例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC证明:延长AD到点E,使DE=AD,联 结 CE.在△ABD和△ECD中, BD=CD(已知)
∠ADB=∠EDC(对顶角相等)
AD=ED(所作)∴ △ABD≌△ECD(S.A.S)∵ 得 EC=AB,∠E=∠1
(全等三角形对应边、对应角相等).又∵ ∠1=∠2(已知),∴∠E=∠2(等量代换)得 EC=AC(等角对等边) ∴ AB=AC(等量代换) 倍长中线法是三角形中线的最基本最常见的一种添辅助线法,这种添辅助线相当于作出与△ABD关于点D对称的图形。小结: 若已知条件有中点,可利用中心对称性构造全等三角形来证明有关线段(或角)的相等。寻
找
规
律已知:如图,AD∥BC,点E是DC的中点,AE平分∠BAD
求证:BE平分∠ABC.F1234小结1例题12 已知:如图17-19,在Rt△ABC中, ∠BAC=90°,D是BC上的一点,AD=AB.
求证: ∠BAD=2∠C. 分析:要证∠BAD=2∠C,只要证∠BAD的一半与∠C相等.
由于AD=AC,因此考 虑作∠BAD的平分线AH.然后将问题转化为证明∠1 =∠C.H1CABD例题12 已知:如图17-19,在Rt△ABC中, ∠BAC=90°,D是BC上的一点,AD=AB.
求证: ∠BAD=2∠C.
证明:过点A作AH⊥BC,垂足为点H.
∵AD=AB(已知),
∴∠BAD=2∠1 (等腰三角形的三线合一),
在△ABC中,
∵∠BAC+∠B+∠C=180°
(三角形的内角和等于180°),
又∵∠BAC=90°(已知),
∴∠B+∠C=90°.
同理∠1 +∠B=90°.
∴∠1 =∠C(同角的余角相等),
∴∠BAD=2∠C.本题证明还有方法吗?
从例题可以想到,要证线段或角的倍半问题,常可利用 “加倍或折半”的方法,转化为证明线段或角相等的问题.本题是利用了等腰三角形的三线合一,即轴对称变换。小结 若条件有角平分线可利用翻折即轴对称性构造全等三角形。例2已知:如图,△ABC中, AB=AC+CD ,∠1=∠2.
求证: ∠C=2∠B分析我思 我进步谈谈你的收获与困惑.评选出今天表现最优秀个人和小组.1、初步了解如何证明线段、角之间的倍半关系.
2、今天学习了两类题型: 1. 具有旋转对称的条件,(中点)2.具有轴对称的条件(角平分线,等腰三角形).
人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。
图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看
知中点、作中线,中线处长加倍看;
底角倍半角分线,有时也作处长线;
线段和差及倍分,延长截取证全等
虚心勤学加苦练,成绩上升成直线。
祝你成功!课外延伸练习部分 41页谢谢合作
在△ABC中,∵AB=AC, ∠1=∠2, ∴BD=CD.
以上成立吗?在△ABC中,
∵ BD=CD, ∠1=∠2
∴ AB=AC 等腰三角形的三线合一如图:现在把上述的条件AB=AC与结论BD=DC互换,得到新命题即为
依据是-----------------。例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC 1.证明线段相等常用哪些方法?2.要证△ABD≌△ACD,
现具备条件? ∠1=∠2
BD=DC
AD=AD能判断三角形全等吗?3.注意到点D是BC的中点,即AD是 △ABC的中线,因此延长AD到E,使DE=AD,联结CE.倍长中线法E例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC由图,你可以得到哪些结论?△ABD≌△ECD,∠E=∠1,
AB=EC ,AB∥EC
∠E=∠2……例11、已知:如图,点D是BC上的一点,BD=CD, ∠1=∠2
求证 AB=AC证明:延长AD到点E,使DE=AD,联 结 CE.在△ABD和△ECD中, BD=CD(已知)
∠ADB=∠EDC(对顶角相等)
AD=ED(所作)∴ △ABD≌△ECD(S.A.S)∵ 得 EC=AB,∠E=∠1
(全等三角形对应边、对应角相等).又∵ ∠1=∠2(已知),∴∠E=∠2(等量代换)得 EC=AC(等角对等边) ∴ AB=AC(等量代换) 倍长中线法是三角形中线的最基本最常见的一种添辅助线法,这种添辅助线相当于作出与△ABD关于点D对称的图形。小结: 若已知条件有中点,可利用中心对称性构造全等三角形来证明有关线段(或角)的相等。寻
找
规
律已知:如图,AD∥BC,点E是DC的中点,AE平分∠BAD
求证:BE平分∠ABC.F1234小结1例题12 已知:如图17-19,在Rt△ABC中, ∠BAC=90°,D是BC上的一点,AD=AB.
求证: ∠BAD=2∠C. 分析:要证∠BAD=2∠C,只要证∠BAD的一半与∠C相等.
由于AD=AC,因此考 虑作∠BAD的平分线AH.然后将问题转化为证明∠1 =∠C.H1CABD例题12 已知:如图17-19,在Rt△ABC中, ∠BAC=90°,D是BC上的一点,AD=AB.
求证: ∠BAD=2∠C.
证明:过点A作AH⊥BC,垂足为点H.
∵AD=AB(已知),
∴∠BAD=2∠1 (等腰三角形的三线合一),
在△ABC中,
∵∠BAC+∠B+∠C=180°
(三角形的内角和等于180°),
又∵∠BAC=90°(已知),
∴∠B+∠C=90°.
同理∠1 +∠B=90°.
∴∠1 =∠C(同角的余角相等),
∴∠BAD=2∠C.本题证明还有方法吗?
从例题可以想到,要证线段或角的倍半问题,常可利用 “加倍或折半”的方法,转化为证明线段或角相等的问题.本题是利用了等腰三角形的三线合一,即轴对称变换。小结 若条件有角平分线可利用翻折即轴对称性构造全等三角形。例2已知:如图,△ABC中, AB=AC+CD ,∠1=∠2.
求证: ∠C=2∠B分析我思 我进步谈谈你的收获与困惑.评选出今天表现最优秀个人和小组.1、初步了解如何证明线段、角之间的倍半关系.
2、今天学习了两类题型: 1. 具有旋转对称的条件,(中点)2.具有轴对称的条件(角平分线,等腰三角形).
人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。
图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看
知中点、作中线,中线处长加倍看;
底角倍半角分线,有时也作处长线;
线段和差及倍分,延长截取证全等
虚心勤学加苦练,成绩上升成直线。
祝你成功!课外延伸练习部分 41页谢谢合作
