正比例函数的图像与性质[上学期]
图片预览




文档简介
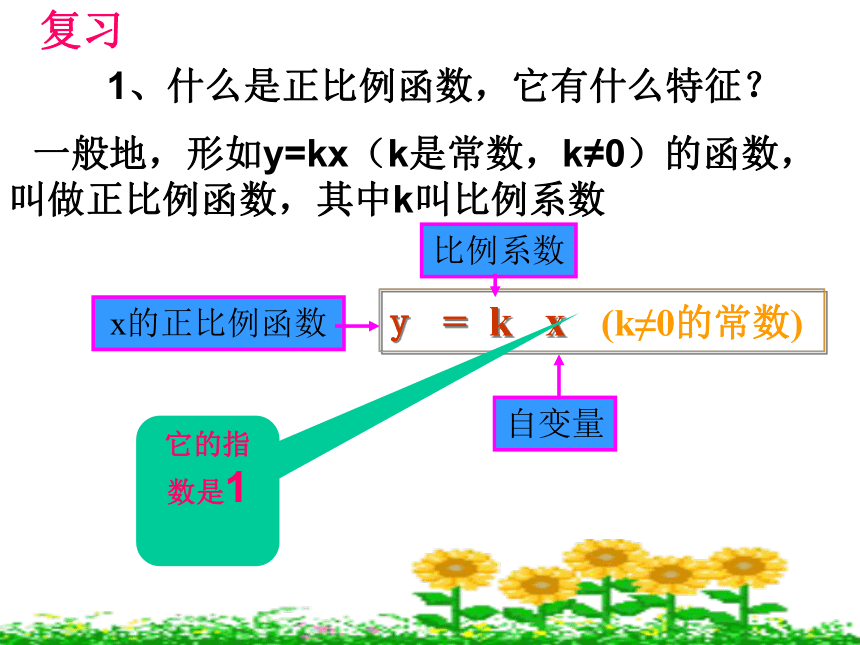
课件25张PPT。正比例函数的图象和性质 一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫比例系数y = k x它的指数是1复习1、什么是正比例函数,它有什么特征?(k≠0的常数)2、若y=(m-1)xm2是关于 x的正比例函数,
则m=______;3、已知y是x的正比例函数,当自变量
x增加8时,函数y 的值减少2,
求正比例函数的解析式复习– 1 为了研究函数图象的方便,我们给出几个定义练
一
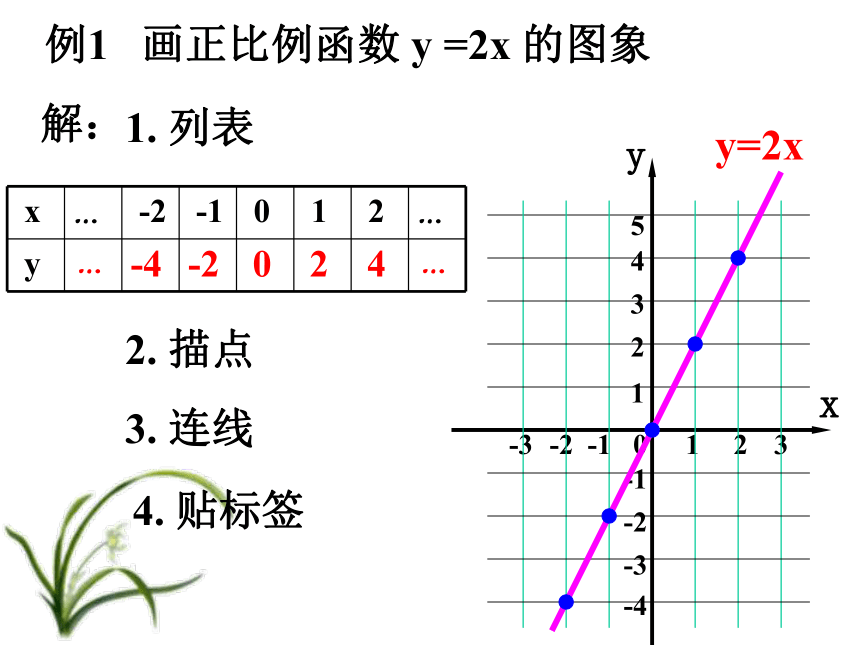
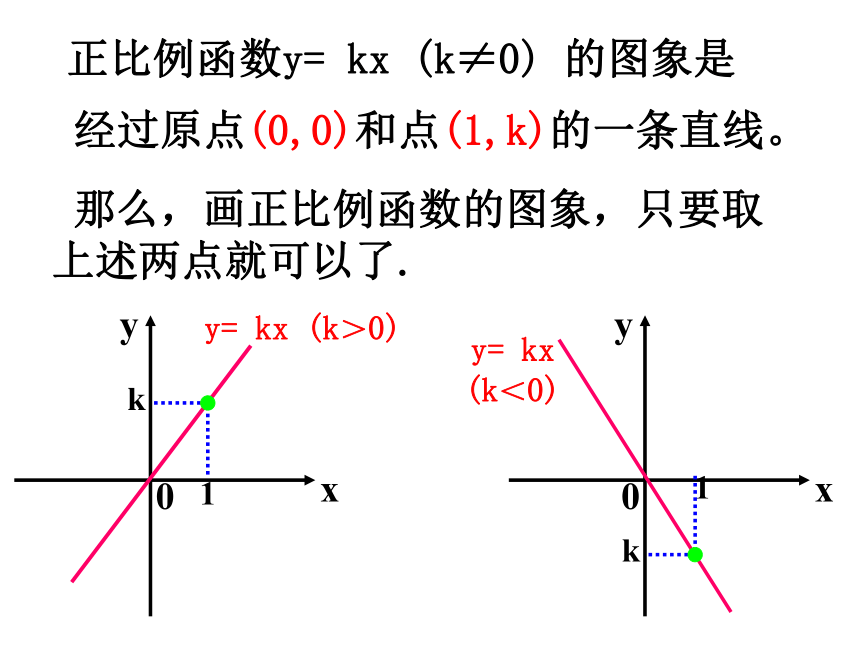
练 y=kx(k是常数,k≠0)是正比例函数的解析式,对于x的每一个确定的值,y都有唯一确定的值与它对应,这样我们就可以得到许多有序实数对,如果我们把这些数对都画在直角坐标平面中,就可以直观地表示函数的对应特征,我们把这些点组成的图形成为函数的图象。下面我们来研究一下,怎么快捷、准确地画出函数的图象?新课-4-2024y=2x例1 画正比例函数 y =2x 的图象解:1. 列表2. 描点3. 连线……4. 贴标签 正比例函数y= kx (k≠0) 的图象是1k1k 经过原点(0,0)和点(1,k)的一条直线。y= kx (k>0)y= kx
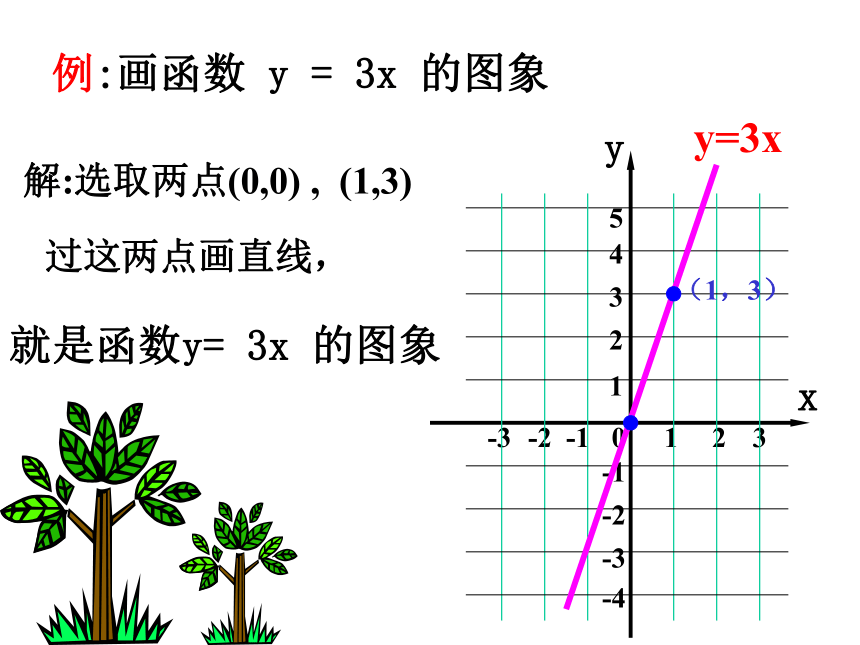
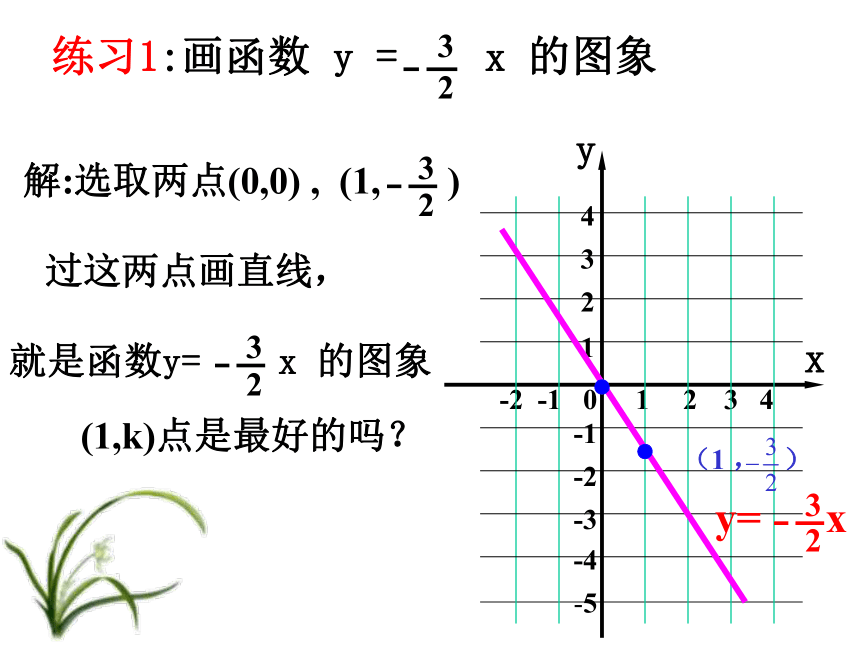
(k<0) 那么,画正比例函数的图象,只要取上述两点就可以了.解:选取两点(0,0) , (1,3)例:画函数 y = 3x 的图象y=3x过这两点画直线,就是函数y= 3x 的图象(1,3)过这两点画直线,(1,k)点是最好的吗?(1 , )过这两点画直线,解:选取两点(0,0) , (2, – 3)(2,– 3)请你动手画一画提示:
1、图象是什么形状的?
2、当自变量x的值增大或减小时,y怎样变化?
3、当k的值变化时,函数图象怎样变化?xy 011比例系数k>0k<0图 象图象位置函数变化总结规律:正比例函数y= kx (k≠0) 的图象是除原点外,在第一、
三 象限除原点外,在第二、
四 象限y随着x
的增大
而增大y随着x
的增大
而减少*当│k│的值增大时,图象靠近y轴经过原点和 (1,k)点的一条直线,并且:练习3、根据下列图象,写出函数关系式:(1) ∠1=∠2(2)4.一辆汽车从A站以每时80千米的速度出发,匀速前进。求出路程y与时间x 的函数解析式,有画出函数的图象解:根据题意,得
y=80x
其中x≥0.取两个点(0,0)和(1,80)
描点、连线.注意两点: 1.x的取值范围
2.由于横、纵轴意义不同, 故单位长度可不同.y=80x(x≥0)5.已知直线 y=kx(k≠0) .2.当直线与x轴成60°时,求k的值.3.当直线与x轴成30°时,求函数的解析式.1.当直线经过点(1,- )时,求函数解析式7、填空
(1)正比例函数 y=kx(k≠0) 的图象是
_____,它一定经过点 和 。直线( 0,0 )( 1,k )(2)如果函数 y= - kx 的图象在一,三象限,那么y = kx 的图象经过 。二、四象限(3)如果 是正比例函数,且y随x的增大而减小,那么m= 。9、正比例函数 的图象是经过
点( )和( )的一条直线 ,它经过第_______象限,即 y 随着 x 的增大而______,如果一个点的纵坐标是—2,那么这个点的横坐标是_______8、函数 y =-7x 的图象经过第______象限, y随x的增大而_______.写出它图象上的三个点的坐标________二、四增大10、正比例函数y =(m—1)x的图象经过一、三象限,则m的取值范围是__________11、滑车以每分1.5米的速度匀速地从轨道的一端滑向另一端,已知轨道的长为7米。
(1)求滑车滑行的路程S(米)和滑行时间t(分)之间的关系和自变量t取值范围;
(2)画出这个函数的图象
(3)根据图象说明当t 增大时S 随着增大还是减小?13、一、今天的收获是什么?二、有什么疑问的地方?三、注意: 1、实际问题求出的函数要注意自变量的取值范围 2、画实际问题的函数图象时,两轴的意义如果不同,单位长度可以不同。作业作业
A,B册/21.4 一课一练21.4 同步21.4
则m=______;3、已知y是x的正比例函数,当自变量
x增加8时,函数y 的值减少2,
求正比例函数的解析式复习– 1 为了研究函数图象的方便,我们给出几个定义练
一
练 y=kx(k是常数,k≠0)是正比例函数的解析式,对于x的每一个确定的值,y都有唯一确定的值与它对应,这样我们就可以得到许多有序实数对,如果我们把这些数对都画在直角坐标平面中,就可以直观地表示函数的对应特征,我们把这些点组成的图形成为函数的图象。下面我们来研究一下,怎么快捷、准确地画出函数的图象?新课-4-2024y=2x例1 画正比例函数 y =2x 的图象解:1. 列表2. 描点3. 连线……4. 贴标签 正比例函数y= kx (k≠0) 的图象是1k1k 经过原点(0,0)和点(1,k)的一条直线。y= kx (k>0)y= kx
(k<0) 那么,画正比例函数的图象,只要取上述两点就可以了.解:选取两点(0,0) , (1,3)例:画函数 y = 3x 的图象y=3x过这两点画直线,就是函数y= 3x 的图象(1,3)过这两点画直线,(1,k)点是最好的吗?(1 , )过这两点画直线,解:选取两点(0,0) , (2, – 3)(2,– 3)请你动手画一画提示:
1、图象是什么形状的?
2、当自变量x的值增大或减小时,y怎样变化?
3、当k的值变化时,函数图象怎样变化?xy 011比例系数k>0k<0图 象图象位置函数变化总结规律:正比例函数y= kx (k≠0) 的图象是除原点外,在第一、
三 象限除原点外,在第二、
四 象限y随着x
的增大
而增大y随着x
的增大
而减少*当│k│的值增大时,图象靠近y轴经过原点和 (1,k)点的一条直线,并且:练习3、根据下列图象,写出函数关系式:(1) ∠1=∠2(2)4.一辆汽车从A站以每时80千米的速度出发,匀速前进。求出路程y与时间x 的函数解析式,有画出函数的图象解:根据题意,得
y=80x
其中x≥0.取两个点(0,0)和(1,80)
描点、连线.注意两点: 1.x的取值范围
2.由于横、纵轴意义不同, 故单位长度可不同.y=80x(x≥0)5.已知直线 y=kx(k≠0) .2.当直线与x轴成60°时,求k的值.3.当直线与x轴成30°时,求函数的解析式.1.当直线经过点(1,- )时,求函数解析式7、填空
(1)正比例函数 y=kx(k≠0) 的图象是
_____,它一定经过点 和 。直线( 0,0 )( 1,k )(2)如果函数 y= - kx 的图象在一,三象限,那么y = kx 的图象经过 。二、四象限(3)如果 是正比例函数,且y随x的增大而减小,那么m= 。9、正比例函数 的图象是经过
点( )和( )的一条直线 ,它经过第_______象限,即 y 随着 x 的增大而______,如果一个点的纵坐标是—2,那么这个点的横坐标是_______8、函数 y =-7x 的图象经过第______象限, y随x的增大而_______.写出它图象上的三个点的坐标________二、四增大10、正比例函数y =(m—1)x的图象经过一、三象限,则m的取值范围是__________11、滑车以每分1.5米的速度匀速地从轨道的一端滑向另一端,已知轨道的长为7米。
(1)求滑车滑行的路程S(米)和滑行时间t(分)之间的关系和自变量t取值范围;
(2)画出这个函数的图象
(3)根据图象说明当t 增大时S 随着增大还是减小?13、一、今天的收获是什么?二、有什么疑问的地方?三、注意: 1、实际问题求出的函数要注意自变量的取值范围 2、画实际问题的函数图象时,两轴的意义如果不同,单位长度可以不同。作业作业
A,B册/21.4 一课一练21.4 同步21.4
