2022--2023学年人教版数学八年级下册 18.2.2菱形的性质课件(共17张PPT)
文档属性
| 名称 | 2022--2023学年人教版数学八年级下册 18.2.2菱形的性质课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 07:18:26 | ||
图片预览

文档简介
(共17张PPT)
18.2.2 菱形的性质
(第一课时)
情景导入
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就变成矩形.
有一个角是直角
那么当平行四边形边发生变化时,会得到什么特殊平行四边形呢?
知识点1: 菱形的性质
探究新知
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
菱形定义:有一组邻边相等的平行四边形叫做菱形.
符号语言:
∵在 ABCD中,AB=AD,
∴ ABCD是菱形.
B
C
D
A
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
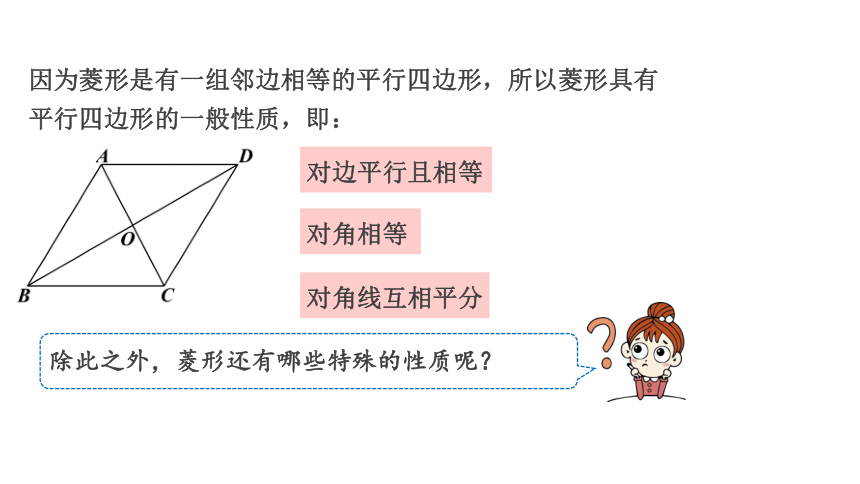
因为菱形是有一组邻边相等的平行四边形,所以菱形具有平行四边形的一般性质,即:
对边平行且相等
除此之外,菱形还有哪些特殊的性质呢?
对角线互相平分
对角相等
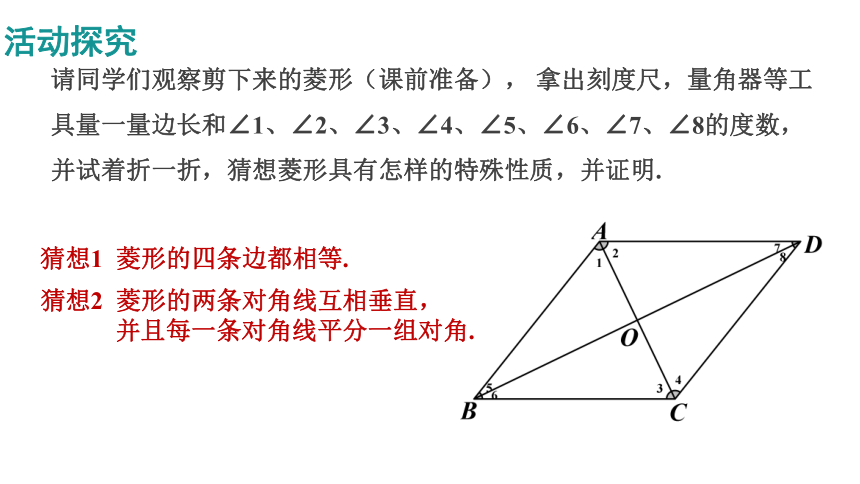
请同学们观察剪下来的菱形(课前准备), 拿出刻度尺,量角器等工具量一量边长和∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8的度数,并试着折一折,猜想菱形具有怎样的特殊性质,并证明.
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
活动探究
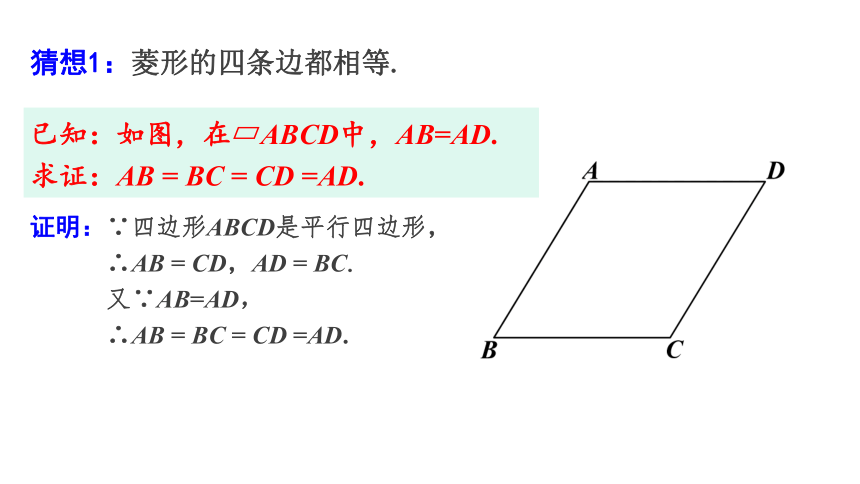
猜想1:菱形的四条边都相等.
已知:如图,在 ABCD中,AB=AD.
求证:AB = BC = CD =AD.
证明:∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC.
又∵AB=AD,
∴AB = BC = CD =AD.
猜想2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:AC⊥BD;
∠1=∠2=∠BAD,
∠3=∠4=∠BCD,
∠5=∠6=∠ABC,
∠7=∠8=∠ADC.
证明:∵四边形ABCD是菱形,
∴AB = AD,OB = OD .
∴AO⊥BD,∠1=∠2= ∠BAD.
即AC⊥BD.
同理可证,∠3=∠4= ∠BCD,
∠5=∠6= ∠ABC,
∠7=∠8= ∠ADC.
边:菱形的四条边都相等,
两组对边分别平行.
角:菱形的两组对角相等.
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD ,
AB∥CD,AD∥BC.
∵ 四边形ABCD是菱形,
∴ ∠BAD=∠BCD,
∠ABC=∠ADC.
菱形的性质
对角线:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
∵四边形ABCD是菱形,
∴ OA=OC= AC,OB=OD= BD,
AC⊥BD,∠1=∠2= ∠BAD,
∠3=∠4= ∠BCD,∠5=∠6= ∠ABC
∠7=∠8= ∠ADC.
典例精析,巩固练习
1.菱形具有而一般平行四边形不具有的性质是( )
A. 对角相等 B. 对边相等
C. 对角线互相垂直 D. 对角线相等
C
2.菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条 C.6条 D.8条
A
当堂检测
菱形的面积
菱形的面积 = 底×高 = 对角线乘积的一半
A
B
C
D
O
E
方法1: S菱形ABCD = 底×高 = BC·AE.
方法2:S菱形ABCD = AC·BD.
3.根据下图填一填:
(1)已知菱形ABCD的周长是 12 cm,那么它的边长是 ____cm.
(2)在菱形ABCD中,∠ABC=100°,则∠BDC=___ °.
3
50
A
B
C
O
D
(3)菱形 ABCD 的两条对角线长分别为 6 cm 和 8 cm,则
菱形的边长是 cm,菱形的面积是 cm2.
5
24
例 如图,菱形花坛 ABCD 的边长为 20 m,∠ABC=60°,
沿着菱形的对角线修建了两条小路 AC 和 BD,求两条小
路的长和花坛的面积.
A
B
C
D
O
小结
菱形的性质
菱形的性质
有关计算
边
1. 周长 = 边长的四倍
2. 面积 = __________________
角
对角线
1. 两组对边平行且相等;
2. 四条边______
两组对角分别_____,邻角互补
1. 两条对角线互相_________;
2. 每一条对角线平分一组对角
相等
相等
垂直平分
两条对角线乘积的一半
作业布置
谢谢观看!
18.2.2 菱形的性质
(第一课时)
情景导入
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就变成矩形.
有一个角是直角
那么当平行四边形边发生变化时,会得到什么特殊平行四边形呢?
知识点1: 菱形的性质
探究新知
思考 如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢
平行四边形
菱形
邻边相等
菱形定义:有一组邻边相等的平行四边形叫做菱形.
符号语言:
∵在 ABCD中,AB=AD,
∴ ABCD是菱形.
B
C
D
A
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
因为菱形是有一组邻边相等的平行四边形,所以菱形具有平行四边形的一般性质,即:
对边平行且相等
除此之外,菱形还有哪些特殊的性质呢?
对角线互相平分
对角相等
请同学们观察剪下来的菱形(课前准备), 拿出刻度尺,量角器等工具量一量边长和∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8的度数,并试着折一折,猜想菱形具有怎样的特殊性质,并证明.
猜想1 菱形的四条边都相等.
猜想2 菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角.
活动探究
猜想1:菱形的四条边都相等.
已知:如图,在 ABCD中,AB=AD.
求证:AB = BC = CD =AD.
证明:∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC.
又∵AB=AD,
∴AB = BC = CD =AD.
猜想2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:AC⊥BD;
∠1=∠2=∠BAD,
∠3=∠4=∠BCD,
∠5=∠6=∠ABC,
∠7=∠8=∠ADC.
证明:∵四边形ABCD是菱形,
∴AB = AD,OB = OD .
∴AO⊥BD,∠1=∠2= ∠BAD.
即AC⊥BD.
同理可证,∠3=∠4= ∠BCD,
∠5=∠6= ∠ABC,
∠7=∠8= ∠ADC.
边:菱形的四条边都相等,
两组对边分别平行.
角:菱形的两组对角相等.
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=AD ,
AB∥CD,AD∥BC.
∵ 四边形ABCD是菱形,
∴ ∠BAD=∠BCD,
∠ABC=∠ADC.
菱形的性质
对角线:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
∵四边形ABCD是菱形,
∴ OA=OC= AC,OB=OD= BD,
AC⊥BD,∠1=∠2= ∠BAD,
∠3=∠4= ∠BCD,∠5=∠6= ∠ABC
∠7=∠8= ∠ADC.
典例精析,巩固练习
1.菱形具有而一般平行四边形不具有的性质是( )
A. 对角相等 B. 对边相等
C. 对角线互相垂直 D. 对角线相等
C
2.菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条 C.6条 D.8条
A
当堂检测
菱形的面积
菱形的面积 = 底×高 = 对角线乘积的一半
A
B
C
D
O
E
方法1: S菱形ABCD = 底×高 = BC·AE.
方法2:S菱形ABCD = AC·BD.
3.根据下图填一填:
(1)已知菱形ABCD的周长是 12 cm,那么它的边长是 ____cm.
(2)在菱形ABCD中,∠ABC=100°,则∠BDC=___ °.
3
50
A
B
C
O
D
(3)菱形 ABCD 的两条对角线长分别为 6 cm 和 8 cm,则
菱形的边长是 cm,菱形的面积是 cm2.
5
24
例 如图,菱形花坛 ABCD 的边长为 20 m,∠ABC=60°,
沿着菱形的对角线修建了两条小路 AC 和 BD,求两条小
路的长和花坛的面积.
A
B
C
D
O
小结
菱形的性质
菱形的性质
有关计算
边
1. 周长 = 边长的四倍
2. 面积 = __________________
角
对角线
1. 两组对边平行且相等;
2. 四条边______
两组对角分别_____,邻角互补
1. 两条对角线互相_________;
2. 每一条对角线平分一组对角
相等
相等
垂直平分
两条对角线乘积的一半
作业布置
谢谢观看!
