几何证明[上学期]
图片预览






文档简介
课件17张PPT。几何证明
复习九年制义务教育课本八年级第一学期基本概念基本技能典型例题基本概念2、命题、定义、定理与公理1、《几何原本》的作者及译者命题:能判断正确或错误的句子叫做命题命题可分为真命题和假命题。命题由题设和结论两个部分组成。定义:说明名词(概念)含义的句子。我们学过的公理有四条定理是真命题,具体见附录(平行线,三角形,平行四边形,等腰三角形,旋转与圆)(1)经过两点有一条直线,并且只有一条直线。(2)在所有连结两点的线中,线段最短。(3)经过已知直线外的一点,有一条并且只有
一条直线与已知直线平行。(4)两条平行线被第三条直线所截,同位角相等。四 条 公 理基本概念3、几何证明几何证明的步骤:(1)根据题意,作出图形并在图上标出
必要的字母或符号;(2)根据题设和结论,结合图形,写出
“已知”和“求证”;(3)通过分析,写出证明过程(每一步
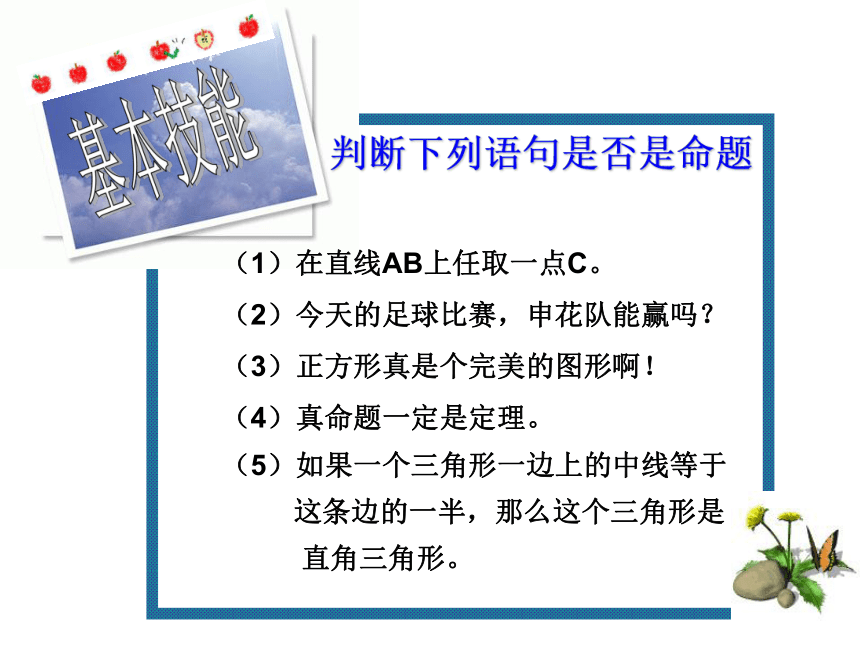
推理都要有依据)。基本技能判断下列语句是否是命题(1)在直线AB上任取一点C。
(2)今天的足球比赛,申花队能赢吗?
(3)正方形真是个完美的图形啊!
(4)真命题一定是定理。
(5)如果一个三角形一边上的中线等于
这条边的一半,那么这个三角形是
直角三角形。 基本技能把下列命题改写成 “如果……,那么……”
形式,并判定该命题是真命题还是假命题。(1)同角的余角相等。
(2)等腰三角形两个底角相等。
(3)直角三角形两锐角互余。
(4)一边上的中线等于这条边一半的三角形
是直角三角形。
(5)有两边及第三边上的高对应相等的两个
三角形全等。 基本技能根据题意画出图形,写出已知、求证(能结合图形,把文字语言写成符号语言)(1)求证:等腰三角形的顶点到两腰的中线
的距离相等。
(2)求证:有两条边及其中一边上的中线对
应相等的两个三角形全等。
(3)求证:一边上的中线等于这条边一半的
三角形是直角三角形。典型例题2、证明举例1、运用推理的计算,求角的度数,线段的
长度,求全等三角形的对数(1)证明角相等在同一个三角形中,用等边对等角。在不同的三角形中,用 全等三角形对应角相等。 (2)证明边相等在同一个三角形中,用等角对等边。在不同的三角形中,用 全等三角形对应边相等。 典型例题2、证明举例(3)证明平行与垂直证明平行时,可转化为证明角的相等。证明垂直,一般证明90度或利用等腰三角形的性质。 (4)证明全等已知两边相等,则找第三边(S.S.S)或夹角(S.A.S)。已知两角相等,则找任一边(A.S.A或A.A.S)已知一边及一角相等,则找任夹边(S.A.S)或任一角(A.A.S或A.S.A)典型例题2、证明举例(5)会添辅助线(i)中线加倍延长(ii)求两条线段的和等于第三条线段,可以
在长的线段上截取,也可把短的线段延长(iii)在直角三角形中添斜边上的中线(iv)圆中常连结半径或垂直于弦的直径。(v)有角平分线时翻折或与平行线构造等腰
三角形(vi)等腰三角形底边上的“三线合一”例1、已知,如图A、B、C、D在一直线上,
AM⊥MB,垂足是M, DN⊥NC,垂足是N,
且AM=ND,AB=CD
求证:CM=CN例2、已知,如图AB=AC, ∠ BAC=90 ° ,
BD⊥DE,垂足是D, CE⊥DE,垂足是E,
F为BC的中点,连结DF、EF
求证:DF=EF且DF⊥EF已知:如图,AD平分∠BAC,DE⊥AC
于点E,且AF+AG=2AE.
求证:∠1与∠2互补.已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长
线交BC于F,若∠ADB=∠FDC
求证:AD=CDGHFABCDE已知:如图,AC=BC,AD=BD ,
∠1=∠2
求证:MN∥ABc作业:同步P144-147
复习九年制义务教育课本八年级第一学期基本概念基本技能典型例题基本概念2、命题、定义、定理与公理1、《几何原本》的作者及译者命题:能判断正确或错误的句子叫做命题命题可分为真命题和假命题。命题由题设和结论两个部分组成。定义:说明名词(概念)含义的句子。我们学过的公理有四条定理是真命题,具体见附录(平行线,三角形,平行四边形,等腰三角形,旋转与圆)(1)经过两点有一条直线,并且只有一条直线。(2)在所有连结两点的线中,线段最短。(3)经过已知直线外的一点,有一条并且只有
一条直线与已知直线平行。(4)两条平行线被第三条直线所截,同位角相等。四 条 公 理基本概念3、几何证明几何证明的步骤:(1)根据题意,作出图形并在图上标出
必要的字母或符号;(2)根据题设和结论,结合图形,写出
“已知”和“求证”;(3)通过分析,写出证明过程(每一步
推理都要有依据)。基本技能判断下列语句是否是命题(1)在直线AB上任取一点C。
(2)今天的足球比赛,申花队能赢吗?
(3)正方形真是个完美的图形啊!
(4)真命题一定是定理。
(5)如果一个三角形一边上的中线等于
这条边的一半,那么这个三角形是
直角三角形。 基本技能把下列命题改写成 “如果……,那么……”
形式,并判定该命题是真命题还是假命题。(1)同角的余角相等。
(2)等腰三角形两个底角相等。
(3)直角三角形两锐角互余。
(4)一边上的中线等于这条边一半的三角形
是直角三角形。
(5)有两边及第三边上的高对应相等的两个
三角形全等。 基本技能根据题意画出图形,写出已知、求证(能结合图形,把文字语言写成符号语言)(1)求证:等腰三角形的顶点到两腰的中线
的距离相等。
(2)求证:有两条边及其中一边上的中线对
应相等的两个三角形全等。
(3)求证:一边上的中线等于这条边一半的
三角形是直角三角形。典型例题2、证明举例1、运用推理的计算,求角的度数,线段的
长度,求全等三角形的对数(1)证明角相等在同一个三角形中,用等边对等角。在不同的三角形中,用 全等三角形对应角相等。 (2)证明边相等在同一个三角形中,用等角对等边。在不同的三角形中,用 全等三角形对应边相等。 典型例题2、证明举例(3)证明平行与垂直证明平行时,可转化为证明角的相等。证明垂直,一般证明90度或利用等腰三角形的性质。 (4)证明全等已知两边相等,则找第三边(S.S.S)或夹角(S.A.S)。已知两角相等,则找任一边(A.S.A或A.A.S)已知一边及一角相等,则找任夹边(S.A.S)或任一角(A.A.S或A.S.A)典型例题2、证明举例(5)会添辅助线(i)中线加倍延长(ii)求两条线段的和等于第三条线段,可以
在长的线段上截取,也可把短的线段延长(iii)在直角三角形中添斜边上的中线(iv)圆中常连结半径或垂直于弦的直径。(v)有角平分线时翻折或与平行线构造等腰
三角形(vi)等腰三角形底边上的“三线合一”例1、已知,如图A、B、C、D在一直线上,
AM⊥MB,垂足是M, DN⊥NC,垂足是N,
且AM=ND,AB=CD
求证:CM=CN例2、已知,如图AB=AC, ∠ BAC=90 ° ,
BD⊥DE,垂足是D, CE⊥DE,垂足是E,
F为BC的中点,连结DF、EF
求证:DF=EF且DF⊥EF已知:如图,AD平分∠BAC,DE⊥AC
于点E,且AF+AG=2AE.
求证:∠1与∠2互补.已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长
线交BC于F,若∠ADB=∠FDC
求证:AD=CDGHFABCDE已知:如图,AC=BC,AD=BD ,
∠1=∠2
求证:MN∥ABc作业:同步P144-147
