证明举例之角相等[上学期]
图片预览



文档简介
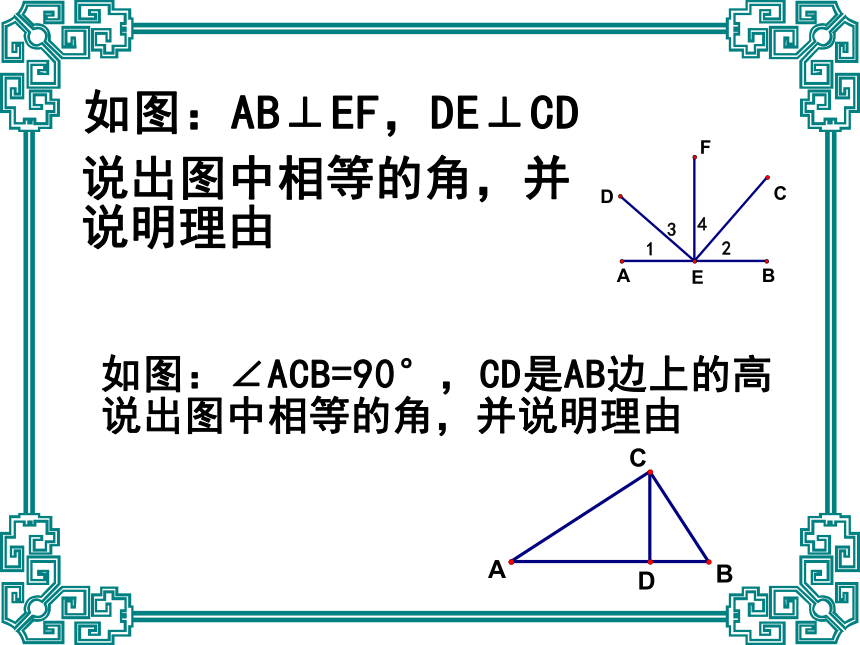
课件15张PPT。22.4 证明举例证明角相等第一课时 (1)根据题意,作出图形并在图
上标出必要的字母或符号。(2)根据题设和结论,结合图
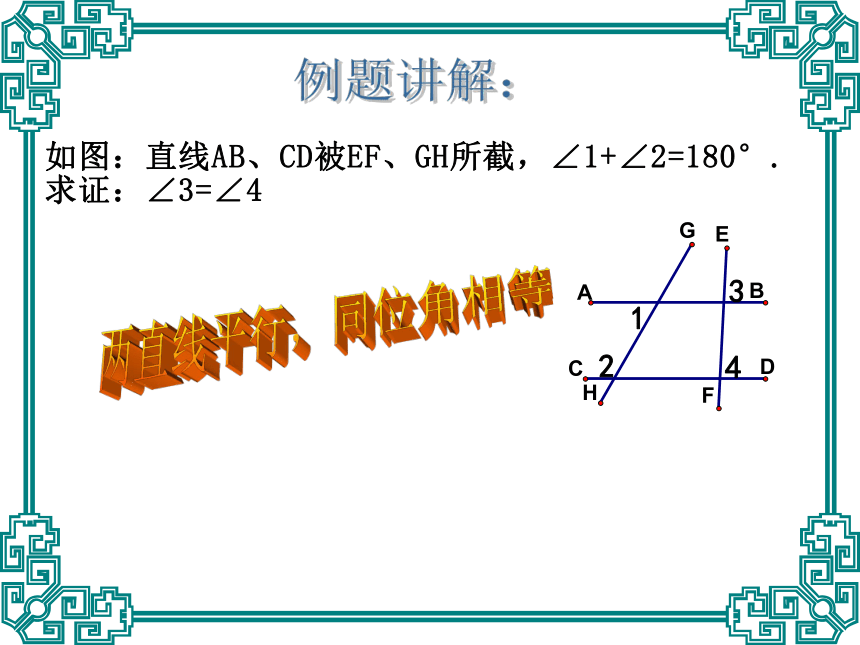
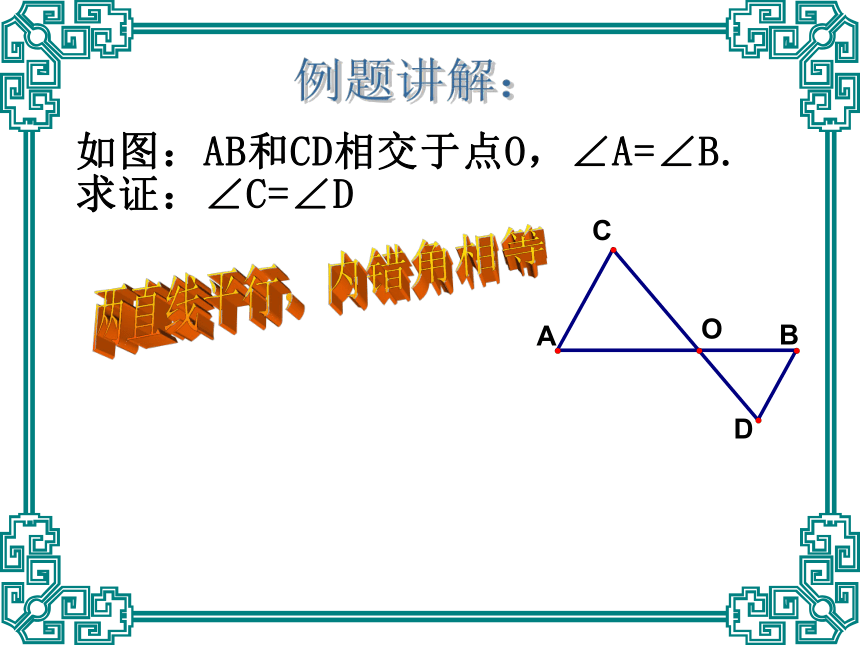
形,写出“已知”和“求证”。(3)通过分析,写出证明过程。复习:证明的步骤是什么?OO两直线平行,同位角相等例题讲解:两直线平行,内错角相等例题讲解:三角形中,等边对等角例题讲解:三角形全等例题讲解:练习:2、已知:⊿ABC的三个内角平分线相交于点O,
过O作OG⊥BC垂足为G
求证:∠BOD=∠COG练习:3、已知:等腰⊿ABC的底边BC上两点P、Q,
按B,P,Q,C的顺序,取BP=QC,
在AB、AC上分别取D,E点,使AD=AE,
DQ与EP交于点O
求证:AO平分∠BAC
练习:4、已知:∠BAD=∠CAD,DE∥AC交AB于E交AB于E,
EF⊥AD交BC的延长线于F
求证:∠B=∠FAC
练习:小结证明“角相等”的思考步骤:第二层次:同(等)角的余(补)角相等 (定理1,2)
两直线平行,同位角相等 (公理4)
两直线平行,内错角相等 (定理12)
第一层次:对顶角相等 (定理3)
角平分线定义第三层次:在同一个三角形中,等边对等角 (定理17)
全等三角形对应角相等 (定理41)
等腰三角形底边上的中线(底边上的高)平分顶角 (定理18)
等边三角形的三个内角都相等,并且每一个内角都等于60度。
(定理20)
在同(等)圆中,如果弦(弦心距,弧)相等,
则所对的圆心角相等。 (定理25,26,27)
平行四边形对角相等 (定理36)
等式性质与等量代换
*一般需要证明的两个角在同一个三角形中,多用等边对等角;*需要证明的两个角在不同的三角形中,*平行线较多,*直角比较多时,多用全等三角形对应角相等;多用平行线的性质;多用等角的余角相等。回家作业:1、B册/22.4(1)
2、同步P110/4(5),P112/4(13),
P113/5(3)(4),P116/6(5),
P118/7(1)
上标出必要的字母或符号。(2)根据题设和结论,结合图
形,写出“已知”和“求证”。(3)通过分析,写出证明过程。复习:证明的步骤是什么?OO两直线平行,同位角相等例题讲解:两直线平行,内错角相等例题讲解:三角形中,等边对等角例题讲解:三角形全等例题讲解:练习:2、已知:⊿ABC的三个内角平分线相交于点O,
过O作OG⊥BC垂足为G
求证:∠BOD=∠COG练习:3、已知:等腰⊿ABC的底边BC上两点P、Q,
按B,P,Q,C的顺序,取BP=QC,
在AB、AC上分别取D,E点,使AD=AE,
DQ与EP交于点O
求证:AO平分∠BAC
练习:4、已知:∠BAD=∠CAD,DE∥AC交AB于E交AB于E,
EF⊥AD交BC的延长线于F
求证:∠B=∠FAC
练习:小结证明“角相等”的思考步骤:第二层次:同(等)角的余(补)角相等 (定理1,2)
两直线平行,同位角相等 (公理4)
两直线平行,内错角相等 (定理12)
第一层次:对顶角相等 (定理3)
角平分线定义第三层次:在同一个三角形中,等边对等角 (定理17)
全等三角形对应角相等 (定理41)
等腰三角形底边上的中线(底边上的高)平分顶角 (定理18)
等边三角形的三个内角都相等,并且每一个内角都等于60度。
(定理20)
在同(等)圆中,如果弦(弦心距,弧)相等,
则所对的圆心角相等。 (定理25,26,27)
平行四边形对角相等 (定理36)
等式性质与等量代换
*一般需要证明的两个角在同一个三角形中,多用等边对等角;*需要证明的两个角在不同的三角形中,*平行线较多,*直角比较多时,多用全等三角形对应角相等;多用平行线的性质;多用等角的余角相等。回家作业:1、B册/22.4(1)
2、同步P110/4(5),P112/4(13),
P113/5(3)(4),P116/6(5),
P118/7(1)
