几何证明之线段相等[上学期]
图片预览




文档简介
课件16张PPT。22.4几何证明举例
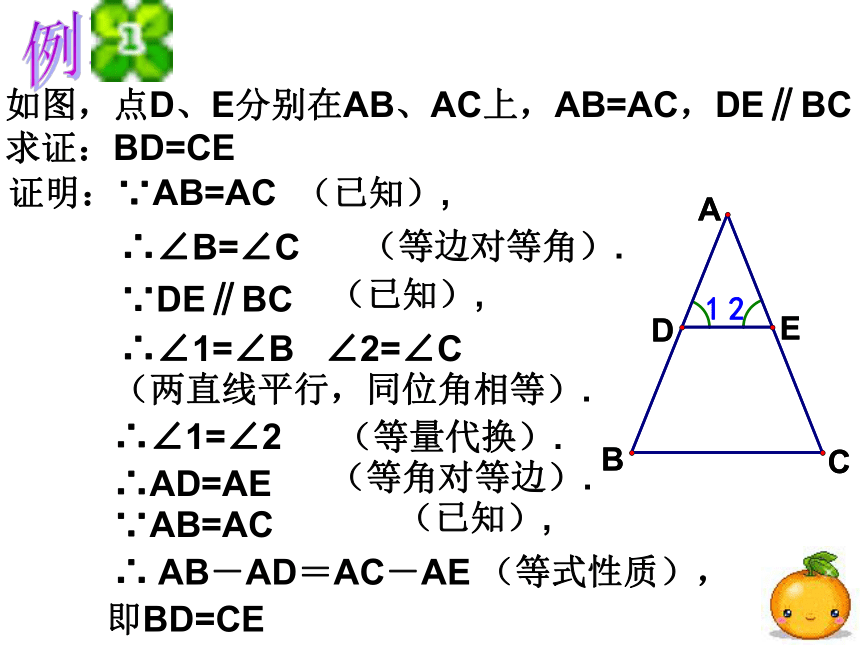
证明线段相等 例1:如图,点D、E分别在AB、AC上,AB=AC,DE∥BC
求证:BD=CE证明:∵AB=AC∴∠B=∠C∵DE∥BC∴∠1=∠B ∠2=∠C
∴∠1=∠2∴AD=AE∵AB=AC∴ AB-AD=AC-AE即BD=CE(已知),(等边对等角).(已知),(两直线平行,同位角相等).(等量代换).(等角对等边).(已知),(等式性质),例题小结:1.三角形中,可用等角对等边证明两条线段相等
2.等量±等量和(差)相等(等式性质)
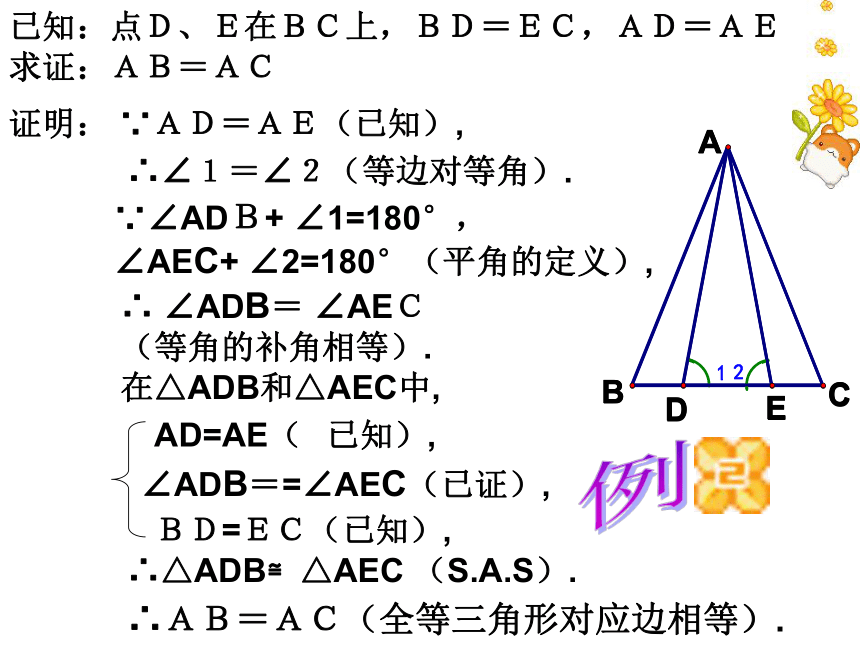
已知:点D、E在BC上,BD=EC,AD=AE
求证:AB=AC∵∠ADB+ ∠1=180°,
∠AEC+ ∠2=180°(平角的定义),证明: ∵AD=AE(已知),∴∠1=∠2(等边对等角).∴ ∠ADB= ∠AEC
(等角的补角相等).在△ADB和△AEC中,AD=AE( 已知),∠ADB==∠AEC(已证),BD=EC(已知),∴△ADB≌△AEC (S.A.S).∴AB=AC(全等三角形对应边相等).例
利用全等三角形证明两条线段相等
例题小结:证明边相等的方法:1.三角形中,等角对等边证明两条
线段相等2.等量±等量和(差)相等
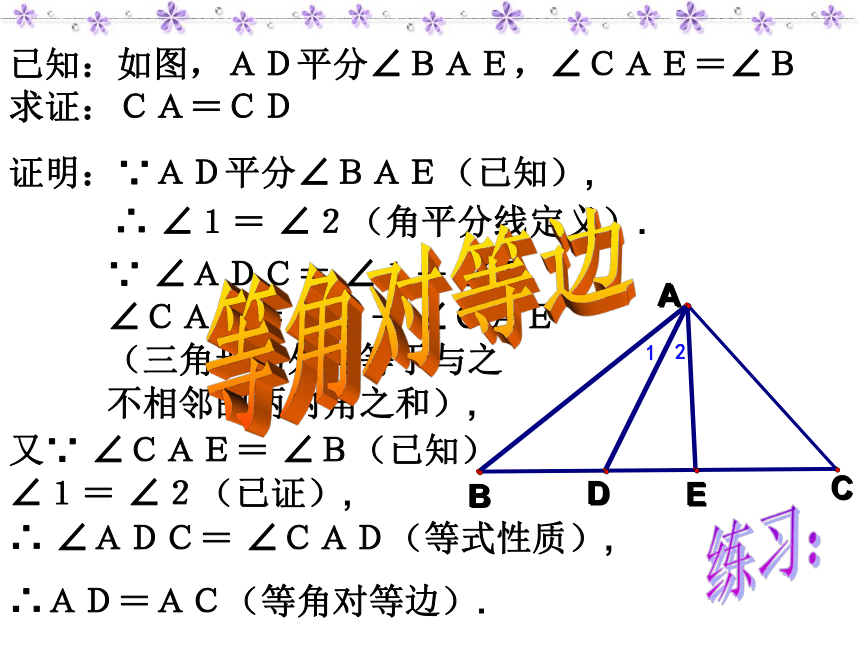
(等式性质)3.利用全等三角形证明两条线段相等练习:已知:如图,AD平分∠BAE,∠CAE=∠B
求证:CA=CD 证明:∵AD平分∠BAE(已知),∴ ∠1= ∠2(角平分线定义).又∵ ∠CAE= ∠B(已知)
∠1= ∠2(已证),∵ ∠ADC= ∠1+ ∠B
∠CAD= ∠2+ ∠CAE
(三角形的外角等于与之
不相邻的两内角之和),∴ ∠ADC= ∠CAD(等式性质), ∴AD=AC(等角对等边).等角对等边已知:如图,在△ABC中,D、E分别在边AB、
AC上,DC与BE相交于点O,且DC=BE,∠1=∠2
求证:AB=AC练习:证明:∵∠ADC+ ∠1=180°
∠AEB+ ∠2=180°(平角的定义) ,又∵∠1=∠2(已知),∴∠ADC=∠AEB
(等角的补角相等).在△ADC和△AEB中∠A=∠A(公共角),∠ADC=∠AEB(已证),DC=BE(已知),∴ △ADC≌△AEB (A.A.S).∴AB=AC (全等三角形的对应边相等).三角形全等如图,△ABC中,∠ABC=45°
H是高AD和高BE的交点
求证:BH=AC三角形全等练习:练习:已知:如图,∠BAC的顶点在⊙O上, ∠BAC的平分线AD过圆心O 求证:AB=AC
三角形全等同圆中等圆心角对等弦证明线段相等的方法:1.三角形中,等角对等边证明两条线段相等2.等量±等量和(差)相等3.利用全等三角形证明两条线段
相等4.利用同圆中等圆心角对等弦
证明两条线段相等如图,F、C是线段BE上两点,BF=CE,
AB=DE,∠B=∠E,QR∥BE
求证:△PQR为等腰三角形思维训练:已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长线
交BC于F,若∠ADB=∠FDC
求证:AD=CD思维训练:已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长线
交BC于F,若∠ADB=∠FDC
求证:AD=CD思维训练:GHFABCDE证明线段相等的方法:1.三角形中,等角对等边证明两条线段相等2.等量±等量和(差)相等3.利用全等三角形证明两条线段
相等4.利用同圆中等圆心角对等弦
证明两条线段相等小结:回家作业:1、A册/22.4(2)2、一课一练P77/1,78/5,P79/1,2,4;P80/5,P81/1,P82/5,6;P83/1;P84/4,63、同步P106-108/1,2;P110/4(6), P111/4(7),P112/4(11)(12),5(1) P113/5(2)(5),P114/5(9),P115/5(12),
P115/6(1), P116/6(2)(3),P117/6(6)(7)(8)
P118/7(3)(4),P119/7(7)(8)
证明线段相等 例1:如图,点D、E分别在AB、AC上,AB=AC,DE∥BC
求证:BD=CE证明:∵AB=AC∴∠B=∠C∵DE∥BC∴∠1=∠B ∠2=∠C
∴∠1=∠2∴AD=AE∵AB=AC∴ AB-AD=AC-AE即BD=CE(已知),(等边对等角).(已知),(两直线平行,同位角相等).(等量代换).(等角对等边).(已知),(等式性质),例题小结:1.三角形中,可用等角对等边证明两条线段相等
2.等量±等量和(差)相等(等式性质)
已知:点D、E在BC上,BD=EC,AD=AE
求证:AB=AC∵∠ADB+ ∠1=180°,
∠AEC+ ∠2=180°(平角的定义),证明: ∵AD=AE(已知),∴∠1=∠2(等边对等角).∴ ∠ADB= ∠AEC
(等角的补角相等).在△ADB和△AEC中,AD=AE( 已知),∠ADB==∠AEC(已证),BD=EC(已知),∴△ADB≌△AEC (S.A.S).∴AB=AC(全等三角形对应边相等).例
利用全等三角形证明两条线段相等
例题小结:证明边相等的方法:1.三角形中,等角对等边证明两条
线段相等2.等量±等量和(差)相等
(等式性质)3.利用全等三角形证明两条线段相等练习:已知:如图,AD平分∠BAE,∠CAE=∠B
求证:CA=CD 证明:∵AD平分∠BAE(已知),∴ ∠1= ∠2(角平分线定义).又∵ ∠CAE= ∠B(已知)
∠1= ∠2(已证),∵ ∠ADC= ∠1+ ∠B
∠CAD= ∠2+ ∠CAE
(三角形的外角等于与之
不相邻的两内角之和),∴ ∠ADC= ∠CAD(等式性质), ∴AD=AC(等角对等边).等角对等边已知:如图,在△ABC中,D、E分别在边AB、
AC上,DC与BE相交于点O,且DC=BE,∠1=∠2
求证:AB=AC练习:证明:∵∠ADC+ ∠1=180°
∠AEB+ ∠2=180°(平角的定义) ,又∵∠1=∠2(已知),∴∠ADC=∠AEB
(等角的补角相等).在△ADC和△AEB中∠A=∠A(公共角),∠ADC=∠AEB(已证),DC=BE(已知),∴ △ADC≌△AEB (A.A.S).∴AB=AC (全等三角形的对应边相等).三角形全等如图,△ABC中,∠ABC=45°
H是高AD和高BE的交点
求证:BH=AC三角形全等练习:练习:已知:如图,∠BAC的顶点在⊙O上, ∠BAC的平分线AD过圆心O 求证:AB=AC
三角形全等同圆中等圆心角对等弦证明线段相等的方法:1.三角形中,等角对等边证明两条线段相等2.等量±等量和(差)相等3.利用全等三角形证明两条线段
相等4.利用同圆中等圆心角对等弦
证明两条线段相等如图,F、C是线段BE上两点,BF=CE,
AB=DE,∠B=∠E,QR∥BE
求证:△PQR为等腰三角形思维训练:已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长线
交BC于F,若∠ADB=∠FDC
求证:AD=CD思维训练:已知:在等腰直角三角形中,∠BAC是直角,
D是AC上一点,AE⊥BD,AE的延长线
交BC于F,若∠ADB=∠FDC
求证:AD=CD思维训练:GHFABCDE证明线段相等的方法:1.三角形中,等角对等边证明两条线段相等2.等量±等量和(差)相等3.利用全等三角形证明两条线段
相等4.利用同圆中等圆心角对等弦
证明两条线段相等小结:回家作业:1、A册/22.4(2)2、一课一练P77/1,78/5,P79/1,2,4;P80/5,P81/1,P82/5,6;P83/1;P84/4,63、同步P106-108/1,2;P110/4(6), P111/4(7),P112/4(11)(12),5(1) P113/5(2)(5),P114/5(9),P115/5(12),
P115/6(1), P116/6(2)(3),P117/6(6)(7)(8)
P118/7(3)(4),P119/7(7)(8)
