几何证明之垂直与平行[上学期]
图片预览



文档简介
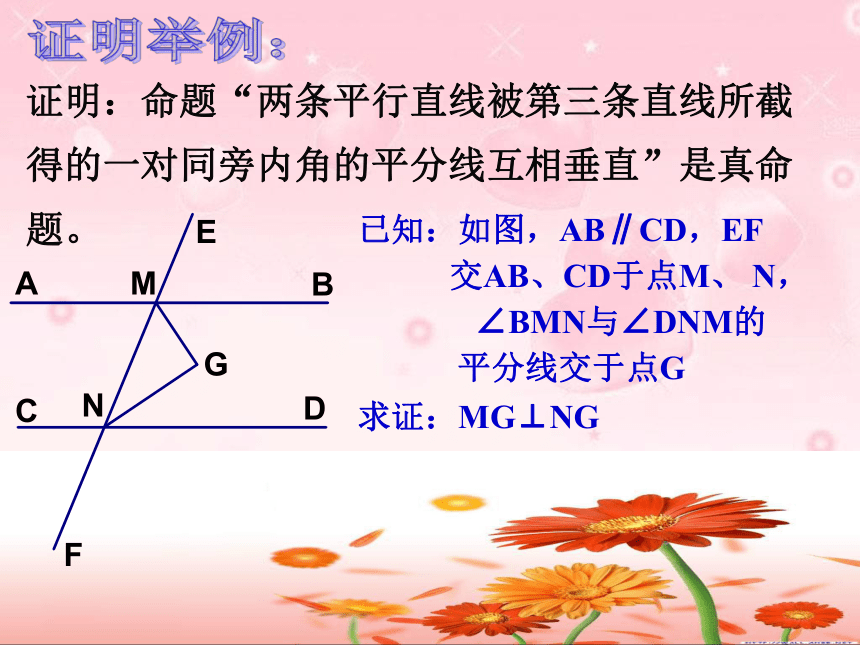
课件20张PPT。22.4 证明举例(3)位置关系—垂直与平行复习:平面内不重合的两条直线的位置关系有什么?相交与平行什么叫垂直? 两条直线相交所成的四个角中,如果有一个角是直角,那么其余三个角都是直角,这是两条直线相交的特殊情况,称为这两条直线互相垂直,交点叫做垂足.新课讲解:你学过的证明两条直线平行或垂直的方法?讨论:证明举例:证明:命题“两条平行直线被第三条直线所截得的一对同旁内角的平分线互相垂直”是真命题。已知:如图,AB∥CD,EF
交AB、CD于点M、 N,
∠BMN与∠DNM的
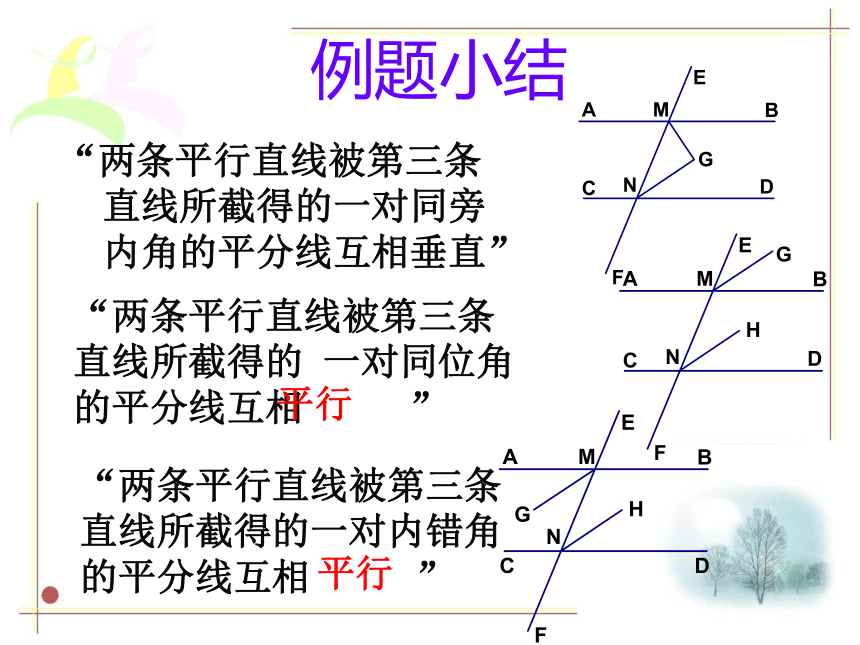
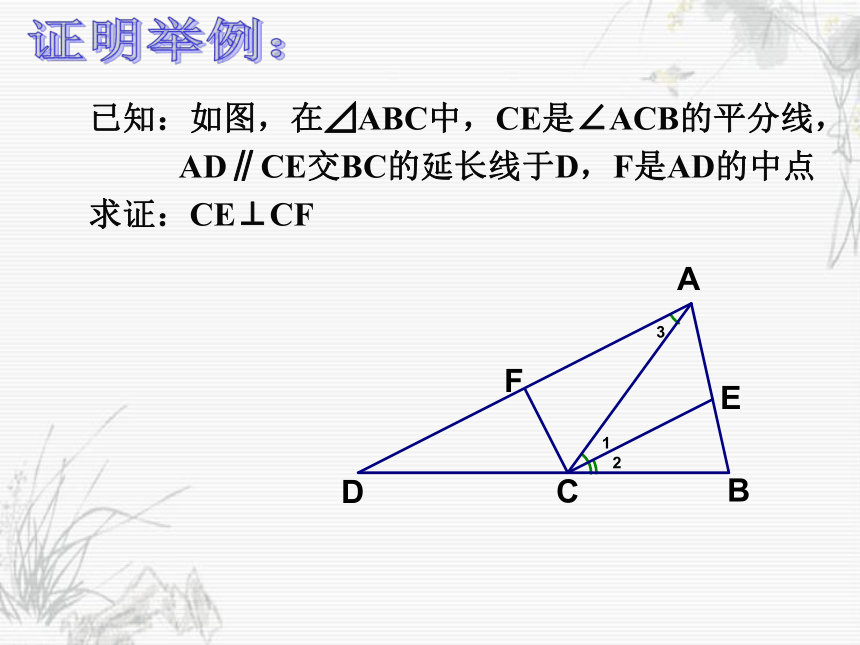
平分线交于点G求证:MG⊥NG例题小结“两条平行直线被第三条直线所截得的一对同旁内角的平分线互相垂直”“两条平行直线被第三条直线所截得的 一对同位角的平分线互相 ”“两条平行直线被第三条直线所截得的一对内错角的平分线互相 ”平行平行证明举例:已知:如图,在⊿ABC中,CE是∠ACB的平分线,
AD∥CE交BC的延长线于D,F是AD的中点
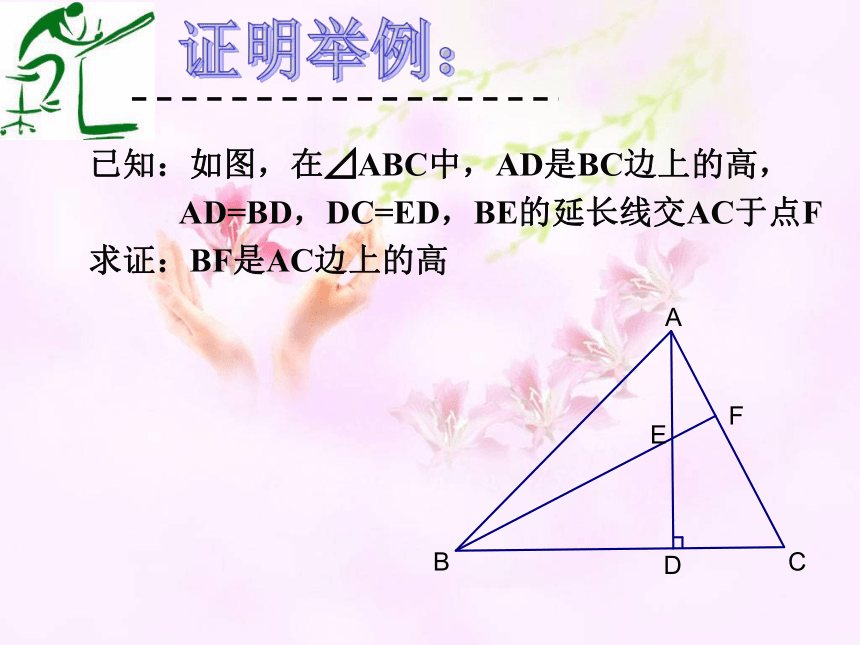
求证:CE⊥CF证明举例:已知:如图,在⊿ABC中,AD是BC边上的高,
AD=BD,DC=ED,BE的延长线交AC于点F
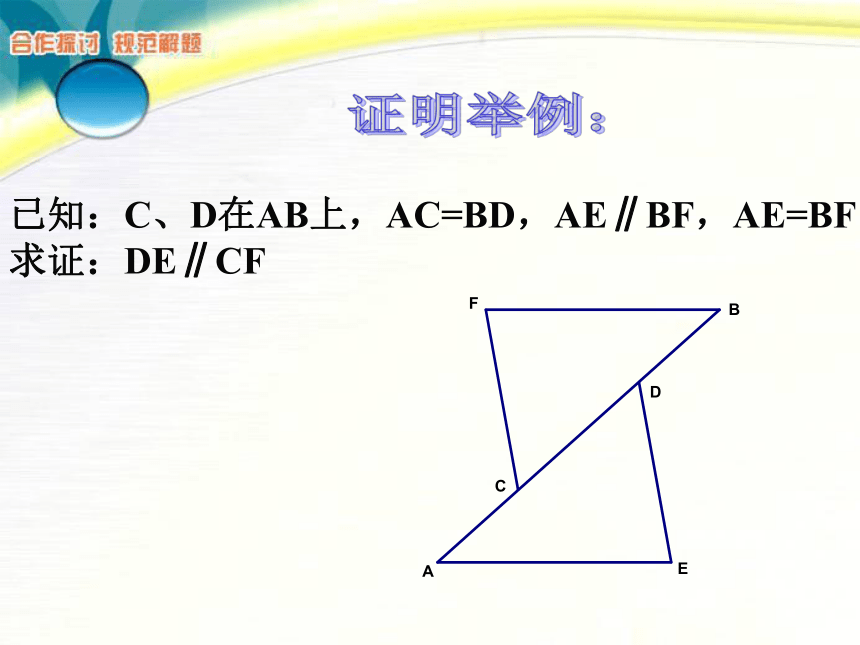
求证:BF是AC边上的高已知:C、D在AB上,AC=BD,AE∥BF,AE=BF
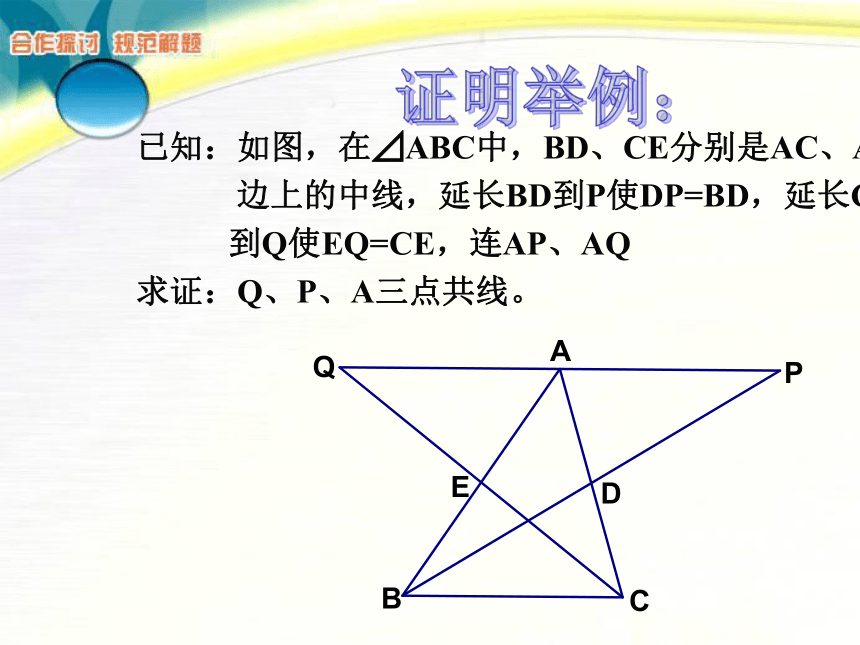
求证:DE∥CF证明举例:证明举例:已知:如图,在⊿ABC中,BD、CE分别是AC、AB
边上的中线,延长BD到P使DP=BD,延长CE
到Q使EQ=CE,连AP、AQ
求证:Q、P、A三点共线。胜者的“钥匙”证明位置关系的一般思路:(1)证明平行转化成角的相等;(2)证明垂直就是证明90度,或利用等腰三角形
的性质 依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.已知:如图,若BD、CE是△ABC的高,
且有BP=AC,AB=CQ
求证:PA⊥AQ小试牛刀:小试牛刀:ZUOYIZUO证明:命题“如果四边形中有一组对角相等,那么这组对角的平分线互相平行(或在一条直线上)”是真命题。已知:如图,△ABC中,AB=AC,∠D=∠1
求证:DE⊥AC小试牛刀:已知:如图,△ABC中,∠ACD=90°,AD
平分∠BAC交BC于D, DE⊥AB于E
求证:AD⊥CE小试牛刀:小试牛刀:ZUOYIZUO已知:如图,△ABC中,AD平分∠BAC
AE=AB,∠1=∠2
求证:EF∥BC小试牛刀:ZUOYIZUO已知:如图,AC=BC,AD=BD ,∠1=∠2
求证:MN∥ABc小试牛刀:ZUOYIZUO已知:如图,AB=AC,DF⊥AB于F,
DE⊥AC于E且DE=DF
求证:EF∥BC本节课你学到什么?小结: 证明两条直线平行,一般转化成证明角的相等 证明两条直线垂直,可以直接证明90度角,或利用等腰三角形“三线合一”的性质及圆中的“垂径定理”的推论。回家作业:1、B册/22.4(3)2、一课一练:P81/2,P83/3,P85/13、同步:P109/4(1)(2),
P110/4(3)(4),
P111/4(8)(9)(10)
P114/5(6)
交AB、CD于点M、 N,
∠BMN与∠DNM的
平分线交于点G求证:MG⊥NG例题小结“两条平行直线被第三条直线所截得的一对同旁内角的平分线互相垂直”“两条平行直线被第三条直线所截得的 一对同位角的平分线互相 ”“两条平行直线被第三条直线所截得的一对内错角的平分线互相 ”平行平行证明举例:已知:如图,在⊿ABC中,CE是∠ACB的平分线,
AD∥CE交BC的延长线于D,F是AD的中点
求证:CE⊥CF证明举例:已知:如图,在⊿ABC中,AD是BC边上的高,
AD=BD,DC=ED,BE的延长线交AC于点F
求证:BF是AC边上的高已知:C、D在AB上,AC=BD,AE∥BF,AE=BF
求证:DE∥CF证明举例:证明举例:已知:如图,在⊿ABC中,BD、CE分别是AC、AB
边上的中线,延长BD到P使DP=BD,延长CE
到Q使EQ=CE,连AP、AQ
求证:Q、P、A三点共线。胜者的“钥匙”证明位置关系的一般思路:(1)证明平行转化成角的相等;(2)证明垂直就是证明90度,或利用等腰三角形
的性质 依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.已知:如图,若BD、CE是△ABC的高,
且有BP=AC,AB=CQ
求证:PA⊥AQ小试牛刀:小试牛刀:ZUOYIZUO证明:命题“如果四边形中有一组对角相等,那么这组对角的平分线互相平行(或在一条直线上)”是真命题。已知:如图,△ABC中,AB=AC,∠D=∠1
求证:DE⊥AC小试牛刀:已知:如图,△ABC中,∠ACD=90°,AD
平分∠BAC交BC于D, DE⊥AB于E
求证:AD⊥CE小试牛刀:小试牛刀:ZUOYIZUO已知:如图,△ABC中,AD平分∠BAC
AE=AB,∠1=∠2
求证:EF∥BC小试牛刀:ZUOYIZUO已知:如图,AC=BC,AD=BD ,∠1=∠2
求证:MN∥ABc小试牛刀:ZUOYIZUO已知:如图,AB=AC,DF⊥AB于F,
DE⊥AC于E且DE=DF
求证:EF∥BC本节课你学到什么?小结: 证明两条直线平行,一般转化成证明角的相等 证明两条直线垂直,可以直接证明90度角,或利用等腰三角形“三线合一”的性质及圆中的“垂径定理”的推论。回家作业:1、B册/22.4(3)2、一课一练:P81/2,P83/3,P85/13、同步:P109/4(1)(2),
P110/4(3)(4),
P111/4(8)(9)(10)
P114/5(6)
