几何证明之添辅助线[上学期]
图片预览




文档简介
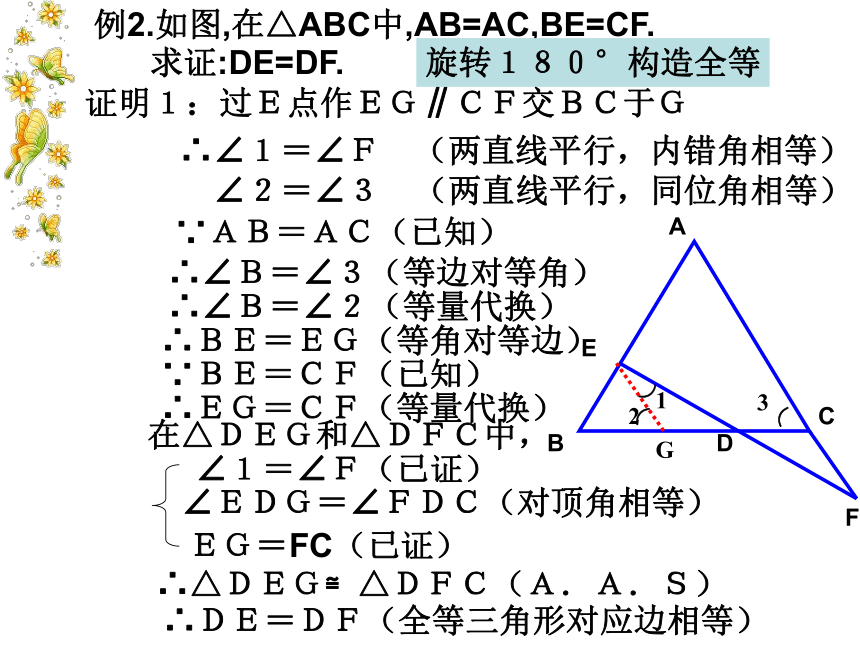
课件16张PPT。复习: 在证明的过程中,由于证明的需要,可以在原来的图形上添画一些线,像这样的线叫做辅助线。辅助线通常画成虚线!添辅助线构造全等例2.如图,在△ABC中,AB=AC,BE=CF.ABDFCEG⌒旋转180°构造全等证明1:过E点作EG∥CF交BC于G∴∠1=∠F (两直线平行,内错角相等)
∠2=∠3 (两直线平行,同位角相等)∵AB=AC(已知)∴∠B=∠3(等边对等角)∴∠B=∠2(等量代换)∴BE=EG(等角对等边)∵BE=CF(已知)∴EG=CF(等量代换)在△DEG和△DFC中, 求证:DE=DF.∠1=∠F(已证)∠EDG=∠FDC(对顶角相等)EG=FC(已证)∴△DEG≌△DFC(A.A.S)∴DE=DF(全等三角形对应边相等)例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.C2ABDFEH⌒证明2:过F点作FH∥BE交BC的延长线于H例3:已知:如图,△ABC中,∠C=2∠B,∠1=∠2.
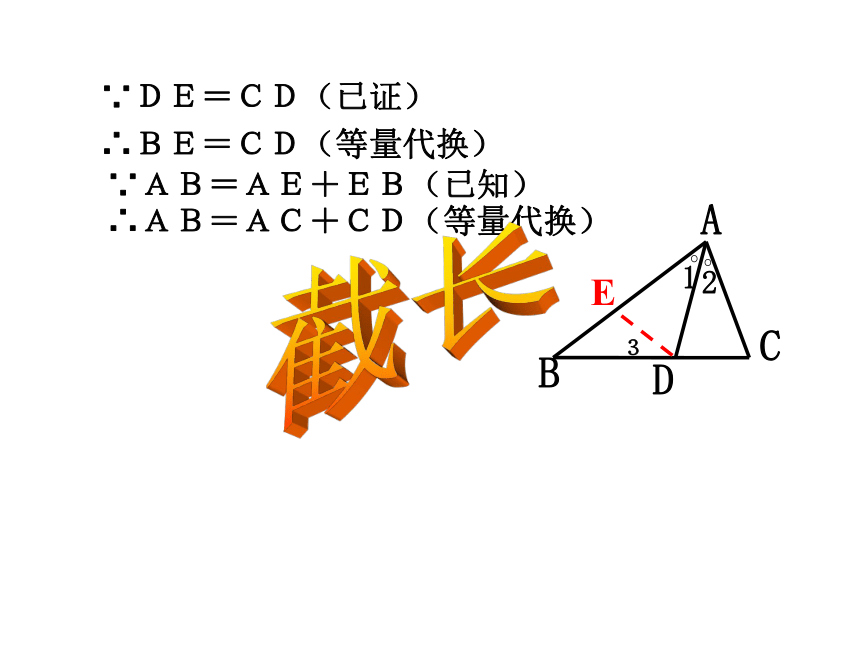
E求证:AB=AC+CD沿着某条直线翻折构造全等证明:在AB上截取AE=AC∴∠AED=∠C,ED=CD
(全等三角形对应边,对应角相等)∵ ∠AED= ∠B+ ∠3
(三角形的外角等于与之不相邻的两内角之和)在△AED和△ACD中,∠1=∠2(已知)AD=AD(公共边)∴△AED≌△ACD(S.A.S)∴BE=ED(等角对等边)AE=AC(已作)3又∵ ∠C=2 ∠B(已知)∴∠B= ∠3(等式性质)3∴BE=CD(等量代换)∵AB=AE+EB(已知)∴AB=AC+CD(等量代换)∵DE=CD(已证)截长例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
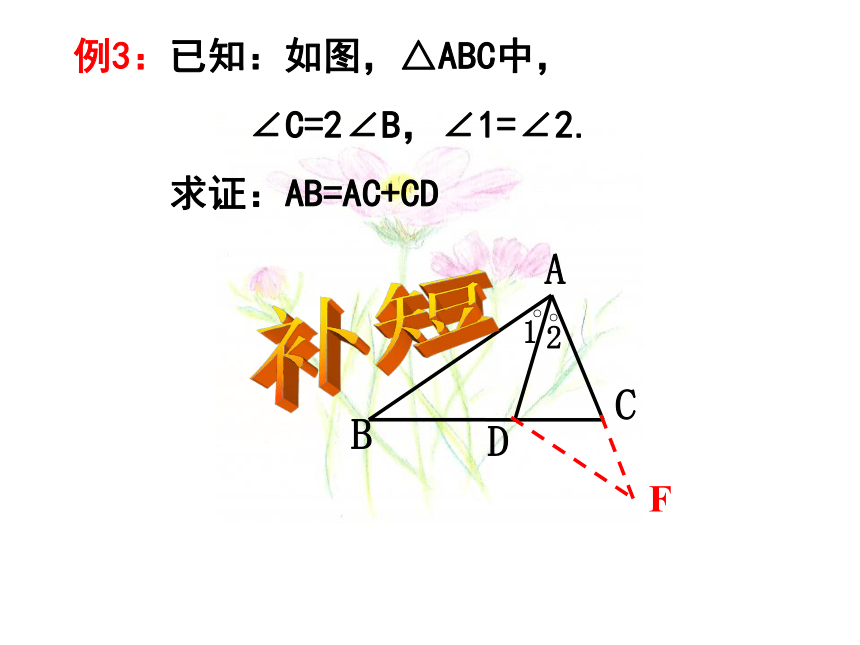
求证:AB=AC+CDF补短证明:延长CF、BA交于点G∵BF平分∠ABC(已知)∴∠1= ∠2(角平分线的定义)∵CF⊥BE(已知)∴ ∠2+ ∠BCF=90°∠1+ ∠G=90°(直角三角形中两锐角互余)∴ ∠BCF= ∠G(等角的余角相等)∵∠BAC=90°(已知)∴BC=BG(等角对等边)∴CF= CG(等腰三角形底边上的高平分底边)∴ ∠CAG=∠BAC=90° ∠3+ ∠G=90°沿着某条直线翻折构造全等∵CF⊥BE(已知)∵∠1+ ∠G=90°(已证)∴ ∠1= ∠3(等角的余角相等)在△CGA和△BEA中,∠1=∠3(已证)∠ CAG= ∠ BAE(已证)∴△CGA≌△BEA(A.S.A)CA=BA(已知)∴CG =BE(全等三角形对应边相等)∵CF= CG(已证)当已知条件中有角平分线或是线段和差问题时,
往往沿角平分线所在的直线或某条直线
将三角形翻折构造全等三角形 例题小结:例5 在△ABC中, ∠1= ∠2,BD=DC 求证:AD⊥BC证明:∴ ∠2= ∠E(等量代换) ∵ ∠1= ∠2(已知)延长AD至E,使DE=AD,连结DEAD=DE(已作)∠3=∠4(对顶角相等)∴△ADB≌△EDC(S.A.S)BD=CD(已知)在△ADB和△EDC中,∴ ∠1=∠E AB=CE
(全等三角形对应角、对应边相等) ∴AC=CE(等角对等边)∴AB=AC(等量代换)∵ ∠1= ∠2(已知)∴AD⊥BC(等腰三角形三线合一)中线加倍法如图,AD∥BC,AE平分∠DAB,BE平分∠CBA,
且C、E、D共线,求证:AB=AD+BC练习:沿着AE所在的直线翻折证明:在AB上截取AF=AD如图, AD∥BC,AE平分∠DAB,BE平分∠CBA,
且C、E、D共线,求证:AB=AD+BC练习:有平行有角平分线必有等腰三角形如图,在△ABC中,AD是BC边上的中线,E是AD
上一点,且BE=AC,延长BE交AC于点F.
求证:AF=EF中线加倍法小 结 :添辅助线的常用技巧1、截长或补短3、有中线常用旋转,
即加倍延长2、有角平分线常用翻折4、圆中经常联结半径或者作垂直于弦的直径(或作弦心距)作业:
1、B册22.4(5)
2、同步P115/5(11) ,
P119/7(5),P120/7(9) (11)
P121/7(15),P123/16
∠2=∠3 (两直线平行,同位角相等)∵AB=AC(已知)∴∠B=∠3(等边对等角)∴∠B=∠2(等量代换)∴BE=EG(等角对等边)∵BE=CF(已知)∴EG=CF(等量代换)在△DEG和△DFC中, 求证:DE=DF.∠1=∠F(已证)∠EDG=∠FDC(对顶角相等)EG=FC(已证)∴△DEG≌△DFC(A.A.S)∴DE=DF(全等三角形对应边相等)例2.如图,在△ABC中,AB=AC,BE=CF.
求证:DE=DF.C2ABDFEH⌒证明2:过F点作FH∥BE交BC的延长线于H例3:已知:如图,△ABC中,∠C=2∠B,∠1=∠2.
E求证:AB=AC+CD沿着某条直线翻折构造全等证明:在AB上截取AE=AC∴∠AED=∠C,ED=CD
(全等三角形对应边,对应角相等)∵ ∠AED= ∠B+ ∠3
(三角形的外角等于与之不相邻的两内角之和)在△AED和△ACD中,∠1=∠2(已知)AD=AD(公共边)∴△AED≌△ACD(S.A.S)∴BE=ED(等角对等边)AE=AC(已作)3又∵ ∠C=2 ∠B(已知)∴∠B= ∠3(等式性质)3∴BE=CD(等量代换)∵AB=AE+EB(已知)∴AB=AC+CD(等量代换)∵DE=CD(已证)截长例3:已知:如图,△ABC中,
∠C=2∠B,∠1=∠2.
求证:AB=AC+CDF补短证明:延长CF、BA交于点G∵BF平分∠ABC(已知)∴∠1= ∠2(角平分线的定义)∵CF⊥BE(已知)∴ ∠2+ ∠BCF=90°∠1+ ∠G=90°(直角三角形中两锐角互余)∴ ∠BCF= ∠G(等角的余角相等)∵∠BAC=90°(已知)∴BC=BG(等角对等边)∴CF= CG(等腰三角形底边上的高平分底边)∴ ∠CAG=∠BAC=90° ∠3+ ∠G=90°沿着某条直线翻折构造全等∵CF⊥BE(已知)∵∠1+ ∠G=90°(已证)∴ ∠1= ∠3(等角的余角相等)在△CGA和△BEA中,∠1=∠3(已证)∠ CAG= ∠ BAE(已证)∴△CGA≌△BEA(A.S.A)CA=BA(已知)∴CG =BE(全等三角形对应边相等)∵CF= CG(已证)当已知条件中有角平分线或是线段和差问题时,
往往沿角平分线所在的直线或某条直线
将三角形翻折构造全等三角形 例题小结:例5 在△ABC中, ∠1= ∠2,BD=DC 求证:AD⊥BC证明:∴ ∠2= ∠E(等量代换) ∵ ∠1= ∠2(已知)延长AD至E,使DE=AD,连结DEAD=DE(已作)∠3=∠4(对顶角相等)∴△ADB≌△EDC(S.A.S)BD=CD(已知)在△ADB和△EDC中,∴ ∠1=∠E AB=CE
(全等三角形对应角、对应边相等) ∴AC=CE(等角对等边)∴AB=AC(等量代换)∵ ∠1= ∠2(已知)∴AD⊥BC(等腰三角形三线合一)中线加倍法如图,AD∥BC,AE平分∠DAB,BE平分∠CBA,
且C、E、D共线,求证:AB=AD+BC练习:沿着AE所在的直线翻折证明:在AB上截取AF=AD如图, AD∥BC,AE平分∠DAB,BE平分∠CBA,
且C、E、D共线,求证:AB=AD+BC练习:有平行有角平分线必有等腰三角形如图,在△ABC中,AD是BC边上的中线,E是AD
上一点,且BE=AC,延长BE交AC于点F.
求证:AF=EF中线加倍法小 结 :添辅助线的常用技巧1、截长或补短3、有中线常用旋转,
即加倍延长2、有角平分线常用翻折4、圆中经常联结半径或者作垂直于弦的直径(或作弦心距)作业:
1、B册22.4(5)
2、同步P115/5(11) ,
P119/7(5),P120/7(9) (11)
P121/7(15),P123/16
