角平分线性质[上学期]
图片预览


文档简介
课件21张PPT。逆命题在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题互为逆命题把一个命题的条件和结论互换就得到它的逆命题,所以每个命题都有逆命题。如果一个定理的逆命题也是一个定理,那么这两个
定理叫做互逆定理不是每一个定理都有逆定理复习:请你尝试:写出两个命题使它们互为逆命题
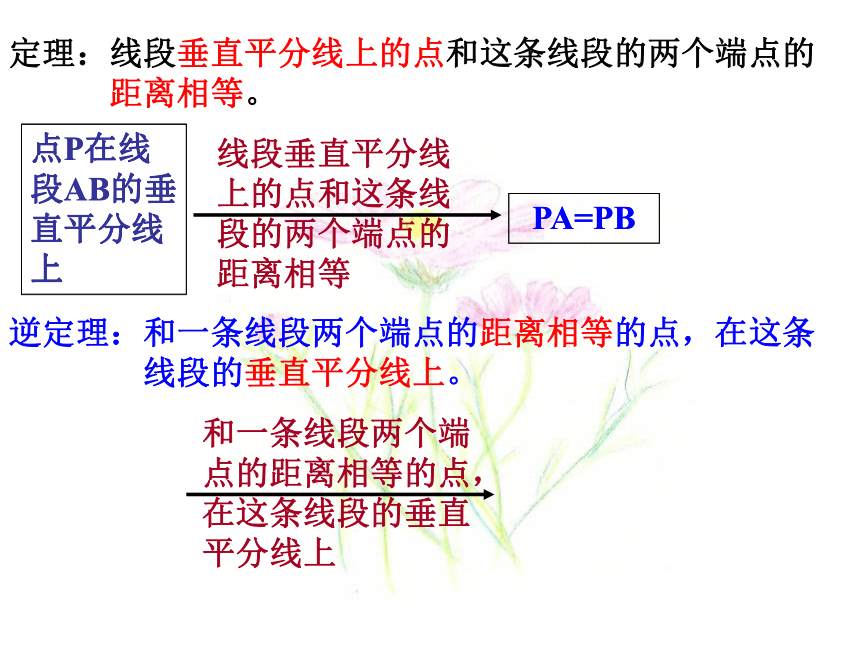
两个定理使它们互为逆定理定理:线段垂直平分线上的点和这条线段的两个端点的
距离相等。PA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点和这条线段的两个端点的距离相等逆定理:和一条线段两个端点的距离相等的点,在这条
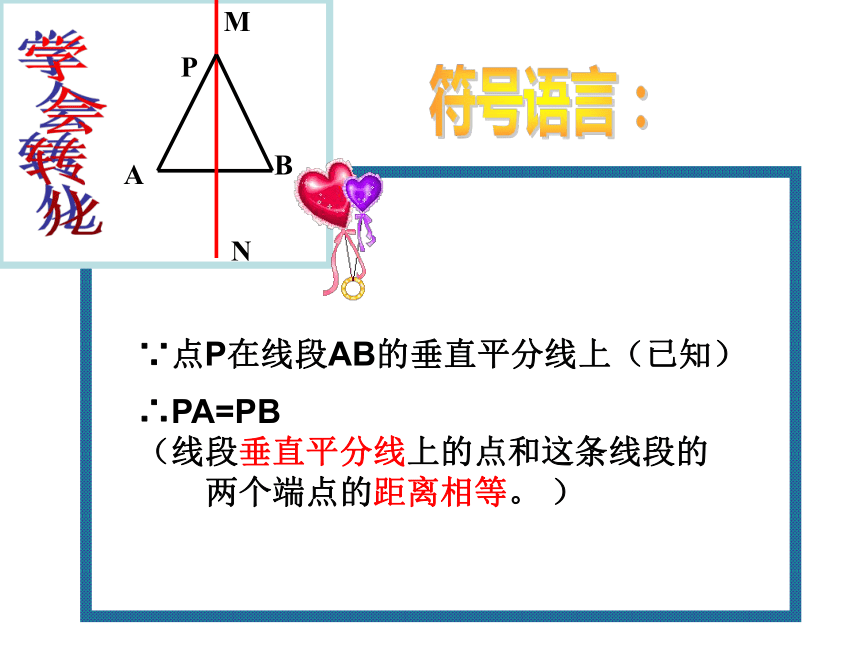
线段的垂直平分线上。点P在线段AB的垂直平分线上PA=PB和一条线段两个端点的距离相等的点,在这条线段的垂直平分线上符号语言:ABPMN∵点P在线段AB的垂直平分线上(已知)∴PA=PB
(线段垂直平分线上的点和这条线段的
两个端点的距离相等。 )
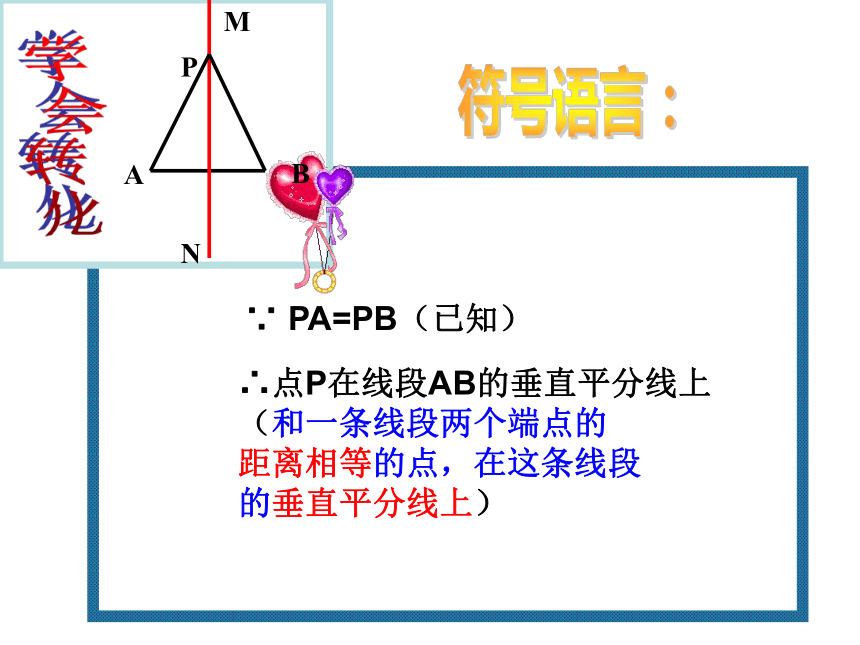
学会转化∵ PA=PB(已知)∴点P在线段AB的垂直平分线上
(和一条线段两个端点的
距离相等的点,在这条线段
的垂直平分线上)
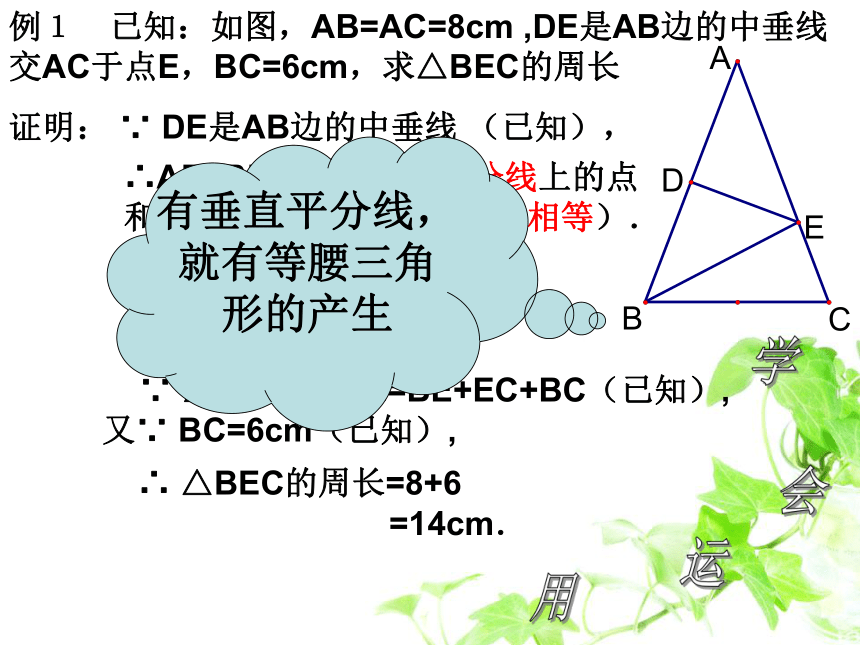
符号语言:ABPMN学会转化例1 已知:如图,AB=AC=8cm ,DE是AB边的中垂线
交AC于点E,BC=6cm,求△BEC的周长证明: ∵ DE是AB边的中垂线 (已知),∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴BE+EC=AE+EC=8cm
(等式性质).∵AC=8cm(已知), ∵ △BEC的周长=BE+EC+BC(已知),
又∵ BC=6cm(已知),∴ △BEC的周长=8+6
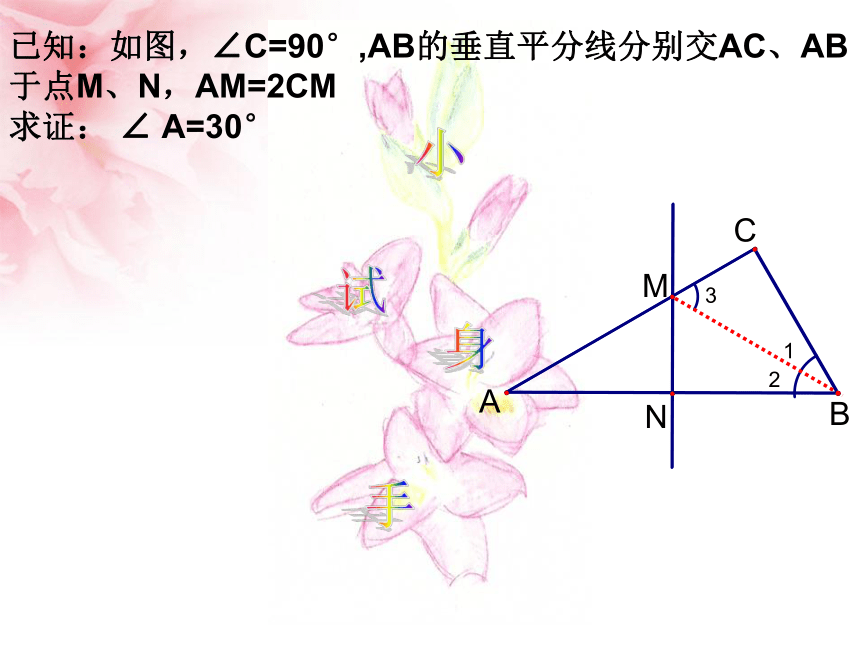
=14cm.有垂直平分线,就有等腰三角形的产生会学运用已知:如图,∠C=90°,AB的垂直平分线分别交AC、AB
于点M、N,AM=2CM
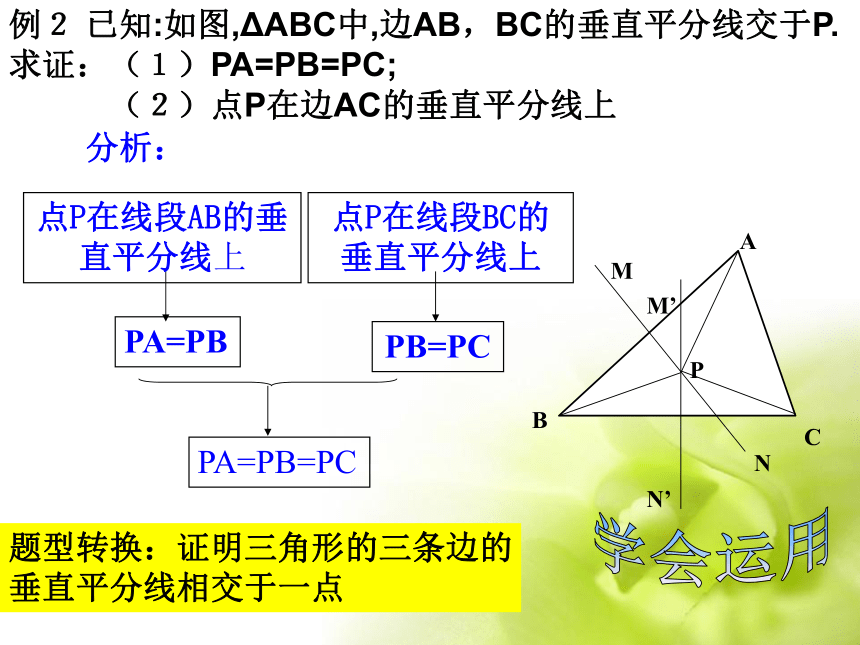
求证: ∠ A=30°小试身手例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上BACMNM’N’P学会运用题型转换:证明三角形的三条边的
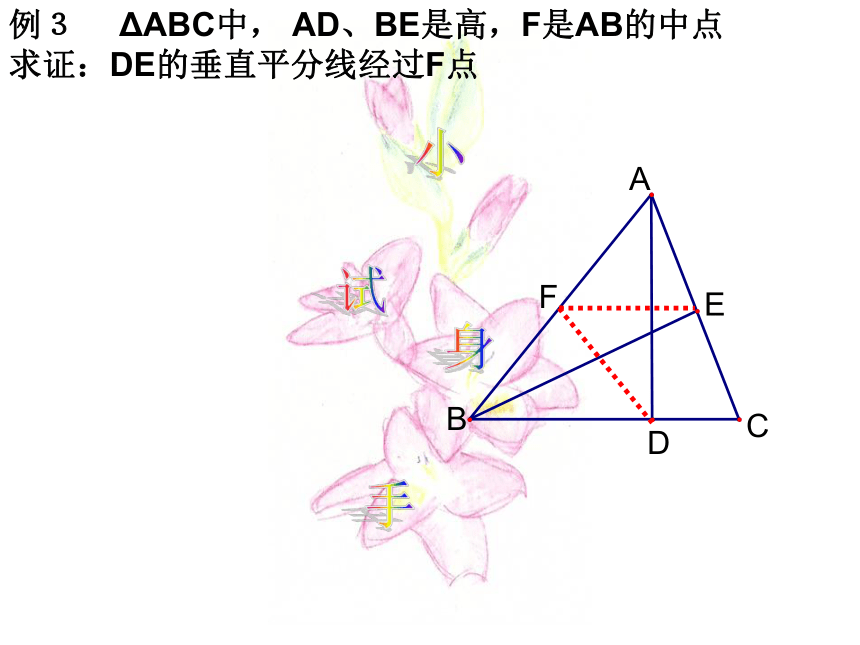
垂直平分线相交于一点小试身手例3 ΔABC中, AD、BE是高,F是AB的中点
求证:DE的垂直平分线经过F点猜测:在角的平分线上的点到这个角的两边的距离相等已知:OC是∠AOB的平分线,点P是OC上一点,
PD⊥OA,PE ⊥ OB,点D、E为垂足
求证:PD=PE证明:∵ PD⊥OA,PE ⊥ OB(已知)∴ ∠PDO= ∠PEO=90° (垂直的定义)∵ OC是∠AOB的平分线∴ ∠1= ∠2 (角平分线的定义)在△PDO和△PEO中∠1= ∠2(已证)∠PDO= ∠PEO(已证)OP=OP(公共边)∴ △PDO≌△PEO(A.A.S )∴PD=PE(全等三角形的对应边相等)定理:角平分线上的点到这个角
的两边的距离相等角平分线的性质符号语言:∵OC平分∠AOB ,点P是OC上一点
PD⊥OA于点D,PE ⊥ OB于点E (已知) ∴PD=PE
(角的平分线上的点到这个角的两边
的距离相等)学会转化想一想:如果点Q到∠AOB的两边的距离相等,那么点Q是否一定在这个角的平分线上?已知:如图,PD⊥OA,PE ⊥ OB,点D、E为垂足
PD=PE
求证:点P在∠AOB的平分线上证明:作射线OP,∵ PD⊥OA,PE ⊥ OB(已知),∴ ∠PDO= ∠PEO=90°
(垂直的定义).在Rt△PDO和Rt △PEO中,OP=OP(公共边)PD=PE(已知)∴Rt△PDO和Rt △PEO(H.L)∴ ∠1= ∠2 (全等三角形的对应角相等)∴点P在∠AOB的平分线上(角平分线的定义)猜测:到一个角的两边距离相等的点,在这个角的平分线上P角平分线的性质逆定理:到一个角两边的距离相等
的点在这个角的角平分线上符号语言:∴P点在∠AOB的平分线上
(到一个角的两边距离相等的点,在这个角的平分线上)学会转化∵ PD⊥OA,PE ⊥ OB,PD = PE(已知),会学运已知:如图,AO平分∠BAC,OD⊥BC,OE⊥AB ,
垂足分别为D、E ,且 OD=OE
求证:CO 平分∠ACB证明:过点O作OF ⊥AC,垂足为F∵ AO平分∠BAC (已知),OE⊥AB(已知)OF ⊥AC(作图)∴OE=OF
(在角的平分线上的点到这个角的两边的距离相等)∵ OD=OE(已知)∴OD=OF(等量代换) ∵ OD⊥BC (已知) OF ⊥AC(作图)∴ CO 平分∠ACB(到一个角的两边的距离相等的点,在这个角的平分线上)请你尝试:证明三角形的三个角的角平分线相交于一点用已知:如图,点B、C在∠MAN的两边AM、AN上,
∠1= ∠2, ∠3= ∠4.如果△PBC的高PD=5cm,那么
1)求点P到AM、AN的距离
2)联结AP,求证:AP平分∠MAN会学运用小试手身在△ABC中,∠ B和∠C的平分线交与点O,OD⊥BC于点
D若△ABC的周长为24,OD=3,则△ ABC的面积是多少EF小试如图,以△ABC的边AB、AC为边向外作等腰直角三角形,
∠EAB= ∠FAC=90°,EC和BF交于点O
求证:OA是∠ EOF的平分线身手
这节课你学到了什么?在角的平分线上的点到这个角的两边的距离相等到一个角的两边距离相等的点,在这个角的平分线上∴P点在∠AOB的平分线上
(在角的平分线上的点到这个角的两边
的距离相等)∵ PD⊥OA于点D,PE ⊥ OB于点E(已知),∵OC平分∠AOB ,点P是OC上一点
PD⊥OA于点D,PE ⊥ OB于点E (已知) ∴PD=PE
(在角的平分线上的点到这个角的两边
的距离相等)小结:
定理叫做互逆定理不是每一个定理都有逆定理复习:请你尝试:写出两个命题使它们互为逆命题
两个定理使它们互为逆定理定理:线段垂直平分线上的点和这条线段的两个端点的
距离相等。PA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点和这条线段的两个端点的距离相等逆定理:和一条线段两个端点的距离相等的点,在这条
线段的垂直平分线上。点P在线段AB的垂直平分线上PA=PB和一条线段两个端点的距离相等的点,在这条线段的垂直平分线上符号语言:ABPMN∵点P在线段AB的垂直平分线上(已知)∴PA=PB
(线段垂直平分线上的点和这条线段的
两个端点的距离相等。 )
学会转化∵ PA=PB(已知)∴点P在线段AB的垂直平分线上
(和一条线段两个端点的
距离相等的点,在这条线段
的垂直平分线上)
符号语言:ABPMN学会转化例1 已知:如图,AB=AC=8cm ,DE是AB边的中垂线
交AC于点E,BC=6cm,求△BEC的周长证明: ∵ DE是AB边的中垂线 (已知),∴AE=BE(线段垂直平分线上的点
和这条线段两个端点的距离相等).
∴BE+EC=AE+EC=8cm
(等式性质).∵AC=8cm(已知), ∵ △BEC的周长=BE+EC+BC(已知),
又∵ BC=6cm(已知),∴ △BEC的周长=8+6
=14cm.有垂直平分线,就有等腰三角形的产生会学运用已知:如图,∠C=90°,AB的垂直平分线分别交AC、AB
于点M、N,AM=2CM
求证: ∠ A=30°小试身手例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上BACMNM’N’P学会运用题型转换:证明三角形的三条边的
垂直平分线相交于一点小试身手例3 ΔABC中, AD、BE是高,F是AB的中点
求证:DE的垂直平分线经过F点猜测:在角的平分线上的点到这个角的两边的距离相等已知:OC是∠AOB的平分线,点P是OC上一点,
PD⊥OA,PE ⊥ OB,点D、E为垂足
求证:PD=PE证明:∵ PD⊥OA,PE ⊥ OB(已知)∴ ∠PDO= ∠PEO=90° (垂直的定义)∵ OC是∠AOB的平分线∴ ∠1= ∠2 (角平分线的定义)在△PDO和△PEO中∠1= ∠2(已证)∠PDO= ∠PEO(已证)OP=OP(公共边)∴ △PDO≌△PEO(A.A.S )∴PD=PE(全等三角形的对应边相等)定理:角平分线上的点到这个角
的两边的距离相等角平分线的性质符号语言:∵OC平分∠AOB ,点P是OC上一点
PD⊥OA于点D,PE ⊥ OB于点E (已知) ∴PD=PE
(角的平分线上的点到这个角的两边
的距离相等)学会转化想一想:如果点Q到∠AOB的两边的距离相等,那么点Q是否一定在这个角的平分线上?已知:如图,PD⊥OA,PE ⊥ OB,点D、E为垂足
PD=PE
求证:点P在∠AOB的平分线上证明:作射线OP,∵ PD⊥OA,PE ⊥ OB(已知),∴ ∠PDO= ∠PEO=90°
(垂直的定义).在Rt△PDO和Rt △PEO中,OP=OP(公共边)PD=PE(已知)∴Rt△PDO和Rt △PEO(H.L)∴ ∠1= ∠2 (全等三角形的对应角相等)∴点P在∠AOB的平分线上(角平分线的定义)猜测:到一个角的两边距离相等的点,在这个角的平分线上P角平分线的性质逆定理:到一个角两边的距离相等
的点在这个角的角平分线上符号语言:∴P点在∠AOB的平分线上
(到一个角的两边距离相等的点,在这个角的平分线上)学会转化∵ PD⊥OA,PE ⊥ OB,PD = PE(已知),会学运已知:如图,AO平分∠BAC,OD⊥BC,OE⊥AB ,
垂足分别为D、E ,且 OD=OE
求证:CO 平分∠ACB证明:过点O作OF ⊥AC,垂足为F∵ AO平分∠BAC (已知),OE⊥AB(已知)OF ⊥AC(作图)∴OE=OF
(在角的平分线上的点到这个角的两边的距离相等)∵ OD=OE(已知)∴OD=OF(等量代换) ∵ OD⊥BC (已知) OF ⊥AC(作图)∴ CO 平分∠ACB(到一个角的两边的距离相等的点,在这个角的平分线上)请你尝试:证明三角形的三个角的角平分线相交于一点用已知:如图,点B、C在∠MAN的两边AM、AN上,
∠1= ∠2, ∠3= ∠4.如果△PBC的高PD=5cm,那么
1)求点P到AM、AN的距离
2)联结AP,求证:AP平分∠MAN会学运用小试手身在△ABC中,∠ B和∠C的平分线交与点O,OD⊥BC于点
D若△ABC的周长为24,OD=3,则△ ABC的面积是多少EF小试如图,以△ABC的边AB、AC为边向外作等腰直角三角形,
∠EAB= ∠FAC=90°,EC和BF交于点O
求证:OA是∠ EOF的平分线身手
这节课你学到了什么?在角的平分线上的点到这个角的两边的距离相等到一个角的两边距离相等的点,在这个角的平分线上∴P点在∠AOB的平分线上
(在角的平分线上的点到这个角的两边
的距离相等)∵ PD⊥OA于点D,PE ⊥ OB于点E(已知),∵OC平分∠AOB ,点P是OC上一点
PD⊥OA于点D,PE ⊥ OB于点E (已知) ∴PD=PE
(在角的平分线上的点到这个角的两边
的距离相等)小结:
