一次函数复习课[下学期]
图片预览








文档简介
课件21张PPT。23.4 一次函数的复习1、关于一次函数的解析式(1)一般地,函数y=kx+b(k、b是常数,k≠0)
叫做关于x 的一次函数。(2)当b=0时,即一次函数y=kx(常数k≠0),
y是x的正比例函数。所以正比例函数是一次
函数的特殊情况。(3)当k=0时,函数 y=b, y是x的常值函数。
特别地当k=0且b = 0时,y = 0表示x轴。这里k的取值范围是不等于零的任何实数;
而自变量x的取值范围(定义域)是一切实数。2、关于确定函数的解析式当化成形如 y = kxa + b的式子后(1)若是一次函数应满足(2)若是正比例函数应满足(3)若是反比例函数应满足(4)若是常值函数应满足2、关于确定函数的解析式用“待定系数法”确定解析式(1)根据已知条件写出含有待定系数的解析式(定型)(2)将x,y的几对值或图象上点的坐标代入上述解析式,
得到以待定系数为未知数的方程或方程组,并解
方程(组),得到待定的系数的值 (定系数)(3)将求出的待定系数代回所求的函数关系式中,得到
所求函数的解析式 (定式)求一次函数的解析式,只要确定k和b两个常数即可;
求正比例函数或反比例函数的解析式,只要确定k
一个系数即可。2、关于确定函数的解析式确定一次函数解析式的三种条件,四种基本类型(1)与已知直线平行 (确定k);(2)在y轴上的截距 (确定b);(3)知道函数过的点 (把已知点坐标代入)。四种类型三种条件(1)过两点(2)过一点且与已知直线平行(3)过一点且知道截距(4)知道截距与已知直线平行3、关于一次函数的图象与性质(1)一次函数y=kx+b(k≠0)的图象是经过
点(0,b)且平行于直线y = kx的一条直线。当k>0时,y随x的增大而增大,这时函数的图象由
左下方朝右上方无限伸展;当k<0时,y随x的增大而减小,这时函数的图象由
左上方朝右下方无限伸展;(2)一次函数y=kx+b(k≠0)的图象
与正比例函数y = kx的图象的比较。3、关于一次函数的图象与性质(2)一次函数y=kx+b(k≠0)的图象
与正比例函数y = kx的图象的比较。当b>0时,y=kx向上平移b个单位,可得y = kx + b的图象;当b<0时,y=kx向下平移|b|= – b个单位,可得
y = kx + b的图象;y = kx + b的图象向左平移a>0个单位,可得到
y = k(x + a)+ b的图象;y = kx + b的图象向右平移a>0个单位,
可得到y = k(x – a)+ b的图象;一般地 y = f(x) 的图象向左(右)平移a>0个单位,
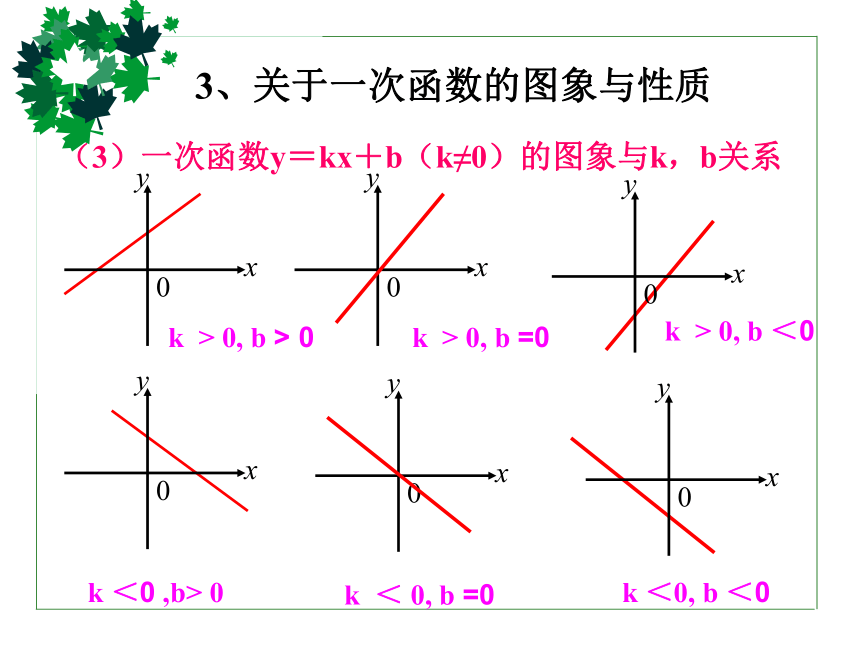
可得到y = f(x + a)[ y = f(x – a) ]的图象.3、关于一次函数的图象与性质(3)一次函数y=kx+b(k≠0)的图象与k,b关系 k > 0, b > 0 k <0 ,b> 0 k > 0, b <0 k < 0, b =0 k <0, b <0 k > 0, b =04、关于直线y = kx + b(k≠0)与
方程、不等式的联系(1)y = kx + b(k≠0)就是一个关于x、y的二元一次方程;(3)若 y > 0则kx + b > 0,同理 y < 1即kx + b < 1; (2)求两直线 y = k1x + b1(k1≠0),y = k2x + b2(k2≠0)
的交点就是解关于x、y的方程组 的解;(4)直线l1: y = k1x + b1在直线l2:y = k2x + b2的上方即
解不等式k1x + b1 > k2x + b2.若y = kx + b在x轴下方
就是解不等式kx + b < 05、关于系数 k、 b的作用(1)k的作用:①增减性; ②平行;
③倾斜的方向;
④倾斜的程度(|k|的大小)。(2)b的作用:与y轴的交点的纵坐标(称截距);(3)k与b共同决定一次函数经过的象限;(4)y = kx +b交x轴于 ,交y轴于(0,b);(5)y = kx + b与坐标轴围成的三角形面积为(6)直线y = k1x +b1与直线y = k2x + b2平行(7)直线y = k1x +b1与直线y = k2x + b2垂直,则k1k2 = – 1 例题精练例1、已知 y – 2与x成正比,当x = 3时,y = 1
求(1)y 与x 的函数关系式;
(2)当x = 6时,y的值;
(3)当y = 8时,x的值;
(4)x为何值时,y > 0.解: (1)∵y – 2与x成正比 ∴y – 2 = kx(k≠0) ∵当 x = 3时,y = 1 ∴1– 2 = 3k, ∴y – 2 = x(2)当x = 6时
(3)当y = 8时
(4)当y > 0时
例题精练例2、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;(4)截距为– 4;
(5)在x轴上的截距为4;(6)它是常值函数;
(7)函数图象过原点;
(8)函数图象不过第二象限;解: (1)∵它是一次函数 ∴ m – 1 ≠0 即m ≠ 1(2) ∵ y随x的增大而减小 ∴m – 1 < 0 即 m < 1 (3)∵它与y = – 2x – 3平行 ∴ m– 1 = – 2即m = – 1 (4)∵截距为– 4 ∴ m – 4 = – 4
即m = 0 (5)∵与x轴截距为4 ∴解得例题精练例2、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;(4)截距为– 4;
(5)在x轴上的截距为4;(6)它是常值函数;
(7)函数图象过原点;
(8)函数图象不过第二象限;解: (6)∵它是常值函数 ∴ m – 1 =0 即m = 1(7) ∵ 它的图象过原点 ∴m – 4 = 0 即 m = 4 (8)∵它的图象不过第二象限 ∴ m–1 >0 或 m = 1 即1≤m≤4时,函数图像不过第二象限.即1<m≤4且m – 4 ≤ 0例题精练例3、设一次函数y = kx + b的图象经过P(3,2),
它与x轴、y轴的正半轴分别交于A、B两点,
OA + BO = 12时,求一次函数的解析式。解: 把x = 3,y = 2代入得 3k + b = 2,∵OA + BO = 12时∴例题精练 例4、A市和B市分别有库存机器12台和6台,现决定
支援C市和D市分别是10台和8台,已知从A市
调运一台机器到C市和D市的运费分别为400元
和800元,从B市调运到C市和D市的运费分别
为300元和500元。
(1)设B市运往C市机器x台,求总运费y与x的函数解析式;
(2) 若要求总运费不超过9千元,问共有几种调运方案;
(3) 求出总运费最低的调运方案,最低运费是多少?解: (1)设B市调往C市x台,调往D市(6 – x)台,
A市运往C市(10 – x)台,运往D市(2 + x)台.y = 300x + 500(6 – x) + 400(10 – x) + 800(2 + x)y = 200x + 8600(0≤x≤6的整数)例题精练 例4、A市和B市分别有库存机器12台和6台,现决定
支援C市和D市分别是10台和8台,已知从A市
调运一台机器到C市和D市的运费分别为400元
和800元,从B市调运到C市和D市的运费分别
为300元和500元。
(1)设B市运往C市机器x台,求总运费y与x的函数解析式;
(2) 若要求总运费不超过9千元,问共有几种调运方案;
(3) 求出总运费最低的调运方案,最低运费是多少?解: (2)∵200x + 8600 ≤9000∴x≤2,∴x = 0,1,2答:共有三种调运方案。(0≤x≤6的整数) (3)∵y = 200x + 8600∴x = 0时,总运费最低为8600元。例题精练例5、一次函数y = kx + b过 y = 3x – 5与 y = – 2x +10
的交点A,y = kx + b交y轴于B,y = – 2x + 10
交x轴于C,若S△ABC = 12,求k与b的值。例题精练例6、反比例函数 的图象和一次函数y = kx – 7
的图象都经过点P(m,2)
求: (1)这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点AB在这个 一
一次函数图象上,顶点CD在这个反比例
函数图象上,两底AD、BC与y轴平行,
且点A和B的横坐标分别为a和a + 2,
求a的值。
例题精练例7、某医药研究所发现一种新药,在实验效果时发现
如果成人按规定剂量服用,那么服药2小时血液中
含药量最高达每毫升6微克(微克 = 10–3毫克),
接着逐步衰减,10小时后血液含药量为每毫升3微
克,每毫升血液中含药量y(微克),随时间x变化
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)在直角坐标平面内画出图象;
(3)如果每毫升血液中含药量为4微克或4微克以上
时在治疗疾病是有效的,那么这个有效时间是
多长 ? 回家作业:补充练习卷一张
双休练习卷一张多做、多练、多思、多问忌懒、忌抄、忌空、忌混
叫做关于x 的一次函数。(2)当b=0时,即一次函数y=kx(常数k≠0),
y是x的正比例函数。所以正比例函数是一次
函数的特殊情况。(3)当k=0时,函数 y=b, y是x的常值函数。
特别地当k=0且b = 0时,y = 0表示x轴。这里k的取值范围是不等于零的任何实数;
而自变量x的取值范围(定义域)是一切实数。2、关于确定函数的解析式当化成形如 y = kxa + b的式子后(1)若是一次函数应满足(2)若是正比例函数应满足(3)若是反比例函数应满足(4)若是常值函数应满足2、关于确定函数的解析式用“待定系数法”确定解析式(1)根据已知条件写出含有待定系数的解析式(定型)(2)将x,y的几对值或图象上点的坐标代入上述解析式,
得到以待定系数为未知数的方程或方程组,并解
方程(组),得到待定的系数的值 (定系数)(3)将求出的待定系数代回所求的函数关系式中,得到
所求函数的解析式 (定式)求一次函数的解析式,只要确定k和b两个常数即可;
求正比例函数或反比例函数的解析式,只要确定k
一个系数即可。2、关于确定函数的解析式确定一次函数解析式的三种条件,四种基本类型(1)与已知直线平行 (确定k);(2)在y轴上的截距 (确定b);(3)知道函数过的点 (把已知点坐标代入)。四种类型三种条件(1)过两点(2)过一点且与已知直线平行(3)过一点且知道截距(4)知道截距与已知直线平行3、关于一次函数的图象与性质(1)一次函数y=kx+b(k≠0)的图象是经过
点(0,b)且平行于直线y = kx的一条直线。当k>0时,y随x的增大而增大,这时函数的图象由
左下方朝右上方无限伸展;当k<0时,y随x的增大而减小,这时函数的图象由
左上方朝右下方无限伸展;(2)一次函数y=kx+b(k≠0)的图象
与正比例函数y = kx的图象的比较。3、关于一次函数的图象与性质(2)一次函数y=kx+b(k≠0)的图象
与正比例函数y = kx的图象的比较。当b>0时,y=kx向上平移b个单位,可得y = kx + b的图象;当b<0时,y=kx向下平移|b|= – b个单位,可得
y = kx + b的图象;y = kx + b的图象向左平移a>0个单位,可得到
y = k(x + a)+ b的图象;y = kx + b的图象向右平移a>0个单位,
可得到y = k(x – a)+ b的图象;一般地 y = f(x) 的图象向左(右)平移a>0个单位,
可得到y = f(x + a)[ y = f(x – a) ]的图象.3、关于一次函数的图象与性质(3)一次函数y=kx+b(k≠0)的图象与k,b关系 k > 0, b > 0 k <0 ,b> 0 k > 0, b <0 k < 0, b =0 k <0, b <0 k > 0, b =04、关于直线y = kx + b(k≠0)与
方程、不等式的联系(1)y = kx + b(k≠0)就是一个关于x、y的二元一次方程;(3)若 y > 0则kx + b > 0,同理 y < 1即kx + b < 1; (2)求两直线 y = k1x + b1(k1≠0),y = k2x + b2(k2≠0)
的交点就是解关于x、y的方程组 的解;(4)直线l1: y = k1x + b1在直线l2:y = k2x + b2的上方即
解不等式k1x + b1 > k2x + b2.若y = kx + b在x轴下方
就是解不等式kx + b < 05、关于系数 k、 b的作用(1)k的作用:①增减性; ②平行;
③倾斜的方向;
④倾斜的程度(|k|的大小)。(2)b的作用:与y轴的交点的纵坐标(称截距);(3)k与b共同决定一次函数经过的象限;(4)y = kx +b交x轴于 ,交y轴于(0,b);(5)y = kx + b与坐标轴围成的三角形面积为(6)直线y = k1x +b1与直线y = k2x + b2平行(7)直线y = k1x +b1与直线y = k2x + b2垂直,则k1k2 = – 1 例题精练例1、已知 y – 2与x成正比,当x = 3时,y = 1
求(1)y 与x 的函数关系式;
(2)当x = 6时,y的值;
(3)当y = 8时,x的值;
(4)x为何值时,y > 0.解: (1)∵y – 2与x成正比 ∴y – 2 = kx(k≠0) ∵当 x = 3时,y = 1 ∴1– 2 = 3k, ∴y – 2 = x(2)当x = 6时
(3)当y = 8时
(4)当y > 0时
例题精练例2、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;(4)截距为– 4;
(5)在x轴上的截距为4;(6)它是常值函数;
(7)函数图象过原点;
(8)函数图象不过第二象限;解: (1)∵它是一次函数 ∴ m – 1 ≠0 即m ≠ 1(2) ∵ y随x的增大而减小 ∴m – 1 < 0 即 m < 1 (3)∵它与y = – 2x – 3平行 ∴ m– 1 = – 2即m = – 1 (4)∵截距为– 4 ∴ m – 4 = – 4
即m = 0 (5)∵与x轴截距为4 ∴解得例题精练例2、已知 y =(m – 1)x + m – 4 ,m为何值时
(1)它是一次函数;(2)y随x的增大而减小;
(3)与y = – 2x – 3平行 ;(4)截距为– 4;
(5)在x轴上的截距为4;(6)它是常值函数;
(7)函数图象过原点;
(8)函数图象不过第二象限;解: (6)∵它是常值函数 ∴ m – 1 =0 即m = 1(7) ∵ 它的图象过原点 ∴m – 4 = 0 即 m = 4 (8)∵它的图象不过第二象限 ∴ m–1 >0 或 m = 1 即1≤m≤4时,函数图像不过第二象限.即1<m≤4且m – 4 ≤ 0例题精练例3、设一次函数y = kx + b的图象经过P(3,2),
它与x轴、y轴的正半轴分别交于A、B两点,
OA + BO = 12时,求一次函数的解析式。解: 把x = 3,y = 2代入得 3k + b = 2,∵OA + BO = 12时∴例题精练 例4、A市和B市分别有库存机器12台和6台,现决定
支援C市和D市分别是10台和8台,已知从A市
调运一台机器到C市和D市的运费分别为400元
和800元,从B市调运到C市和D市的运费分别
为300元和500元。
(1)设B市运往C市机器x台,求总运费y与x的函数解析式;
(2) 若要求总运费不超过9千元,问共有几种调运方案;
(3) 求出总运费最低的调运方案,最低运费是多少?解: (1)设B市调往C市x台,调往D市(6 – x)台,
A市运往C市(10 – x)台,运往D市(2 + x)台.y = 300x + 500(6 – x) + 400(10 – x) + 800(2 + x)y = 200x + 8600(0≤x≤6的整数)例题精练 例4、A市和B市分别有库存机器12台和6台,现决定
支援C市和D市分别是10台和8台,已知从A市
调运一台机器到C市和D市的运费分别为400元
和800元,从B市调运到C市和D市的运费分别
为300元和500元。
(1)设B市运往C市机器x台,求总运费y与x的函数解析式;
(2) 若要求总运费不超过9千元,问共有几种调运方案;
(3) 求出总运费最低的调运方案,最低运费是多少?解: (2)∵200x + 8600 ≤9000∴x≤2,∴x = 0,1,2答:共有三种调运方案。(0≤x≤6的整数) (3)∵y = 200x + 8600∴x = 0时,总运费最低为8600元。例题精练例5、一次函数y = kx + b过 y = 3x – 5与 y = – 2x +10
的交点A,y = kx + b交y轴于B,y = – 2x + 10
交x轴于C,若S△ABC = 12,求k与b的值。例题精练例6、反比例函数 的图象和一次函数y = kx – 7
的图象都经过点P(m,2)
求: (1)这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点AB在这个 一
一次函数图象上,顶点CD在这个反比例
函数图象上,两底AD、BC与y轴平行,
且点A和B的横坐标分别为a和a + 2,
求a的值。
例题精练例7、某医药研究所发现一种新药,在实验效果时发现
如果成人按规定剂量服用,那么服药2小时血液中
含药量最高达每毫升6微克(微克 = 10–3毫克),
接着逐步衰减,10小时后血液含药量为每毫升3微
克,每毫升血液中含药量y(微克),随时间x变化
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)在直角坐标平面内画出图象;
(3)如果每毫升血液中含药量为4微克或4微克以上
时在治疗疾病是有效的,那么这个有效时间是
多长 ? 回家作业:补充练习卷一张
双休练习卷一张多做、多练、多思、多问忌懒、忌抄、忌空、忌混
