相似三角形的判定[上学期]
图片预览



文档简介
课件11张PPT。初中几何
5.4 三角形相似的判定(1)一、复习引入。1、相似三角形的定义是什么? 如果那么ΔABC∽ΔA/B/C/ 2、相似三角形与全等三角形有什么内在的联系呢? 全等三角形是相似比为1的特殊的相似三角形。 3、平行于三角形一边的直线与三角形的其它两边(或两边的延长线)相交,所截得的三角形与原三角形相似。分析:要证两个三角形相似,
目前只有两个途径。一个是
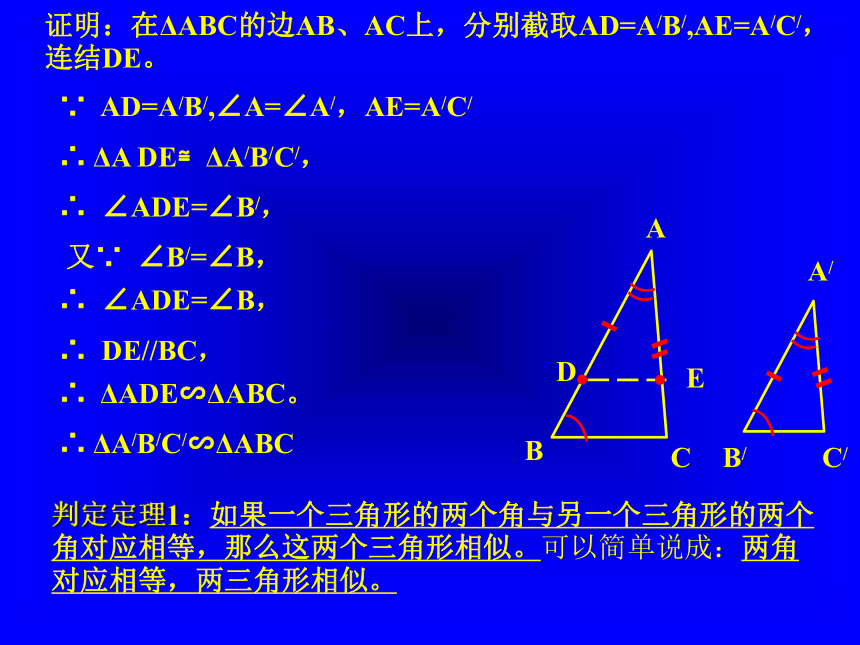
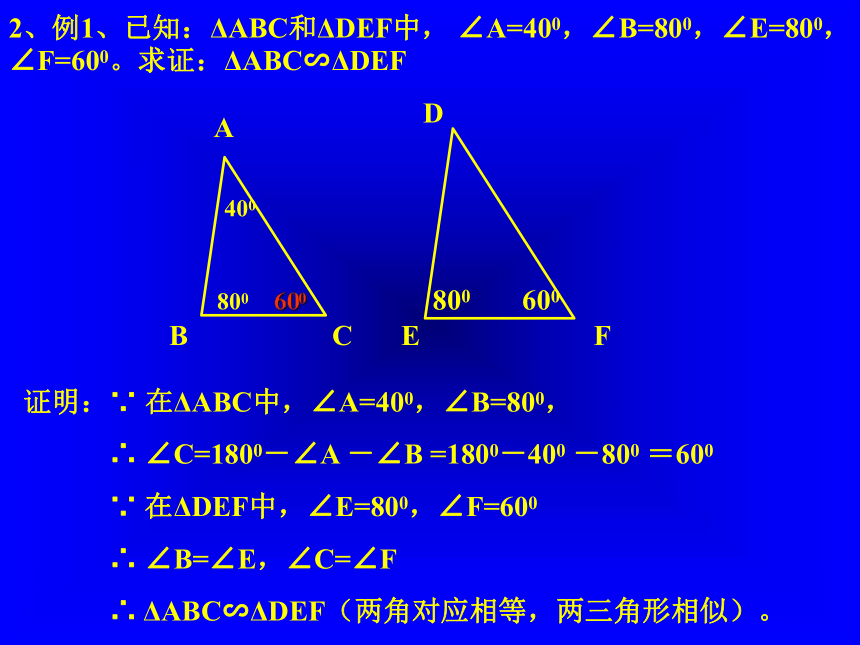
三角形相似的定义,(显然条件不具备);二个是上节课学习的利用平行线来判定三角形相似的定理。为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢?二、新课教学。 1、命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。(把小的三角形移动到大的三角形上)。怎样实现移动呢?证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/,连结DE。判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A/B/,∠A=∠A/,AE=A/C/∴ ΔA DE≌ΔA/B/C/,∴ ∠ADE=∠B/,又∵ ∠B/=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA/B/C/∽ΔABC2、例1、已知:ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800, ∠F=600。求证:ΔABC∽ΔDEF 证明:∵ 在ΔABC中,∠A=400,∠B=800,
∴ ∠C=1800-∠A -∠B =1800-400 -800 =600
∵ 在ΔDEF中,∠E=800,∠F=600
∴ ∠B=∠E,∠C=∠F
∴ ΔABC∽ΔDEF(两角对应相等,两三角形相似)。400 800 800 600 600 3、课堂练习。(1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?(2)已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/。
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/。4、例2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:5、延伸练习。已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.课外思考题: 如图,在ΔABC中 ,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与 ΔABC相似? (提示:图有两种可能)三、课堂小结。四、课外作业。
1、教材P229,2题;P238,3、4、题
2、课外思考题。(见所发题单)1、相似三角形的判定定理1:两角对应相等,两三角形相似。2、母子相似定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。同学们,再见!广汉市金雁中学
李良友
2002年5月
5.4 三角形相似的判定(1)一、复习引入。1、相似三角形的定义是什么? 如果那么ΔABC∽ΔA/B/C/ 2、相似三角形与全等三角形有什么内在的联系呢? 全等三角形是相似比为1的特殊的相似三角形。 3、平行于三角形一边的直线与三角形的其它两边(或两边的延长线)相交,所截得的三角形与原三角形相似。分析:要证两个三角形相似,
目前只有两个途径。一个是
三角形相似的定义,(显然条件不具备);二个是上节课学习的利用平行线来判定三角形相似的定理。为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢?二、新课教学。 1、命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。(把小的三角形移动到大的三角形上)。怎样实现移动呢?证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/,连结DE。判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。∵ AD=A/B/,∠A=∠A/,AE=A/C/∴ ΔA DE≌ΔA/B/C/,∴ ∠ADE=∠B/,又∵ ∠B/=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ ΔADE∽ΔABC。∴ ΔA/B/C/∽ΔABC2、例1、已知:ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800, ∠F=600。求证:ΔABC∽ΔDEF 证明:∵ 在ΔABC中,∠A=400,∠B=800,
∴ ∠C=1800-∠A -∠B =1800-400 -800 =600
∵ 在ΔDEF中,∠E=800,∠F=600
∴ ∠B=∠E,∠C=∠F
∴ ΔABC∽ΔDEF(两角对应相等,两三角形相似)。400 800 800 600 600 3、课堂练习。(1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500,∠A/=550,这两个三角形相似吗?为什么?(2)已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:①如果∠A=∠A/,那么ΔABC∽ΔA/B/C/。
②如果∠B=∠B/,那么ΔABC∽ΔA/B/C/。4、例2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:5、延伸练习。已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.课外思考题: 如图,在ΔABC中 ,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与 ΔABC相似? (提示:图有两种可能)三、课堂小结。四、课外作业。
1、教材P229,2题;P238,3、4、题
2、课外思考题。(见所发题单)1、相似三角形的判定定理1:两角对应相等,两三角形相似。2、母子相似定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。同学们,再见!广汉市金雁中学
李良友
2002年5月
