解直角三角形[上学期]
图片预览


文档简介
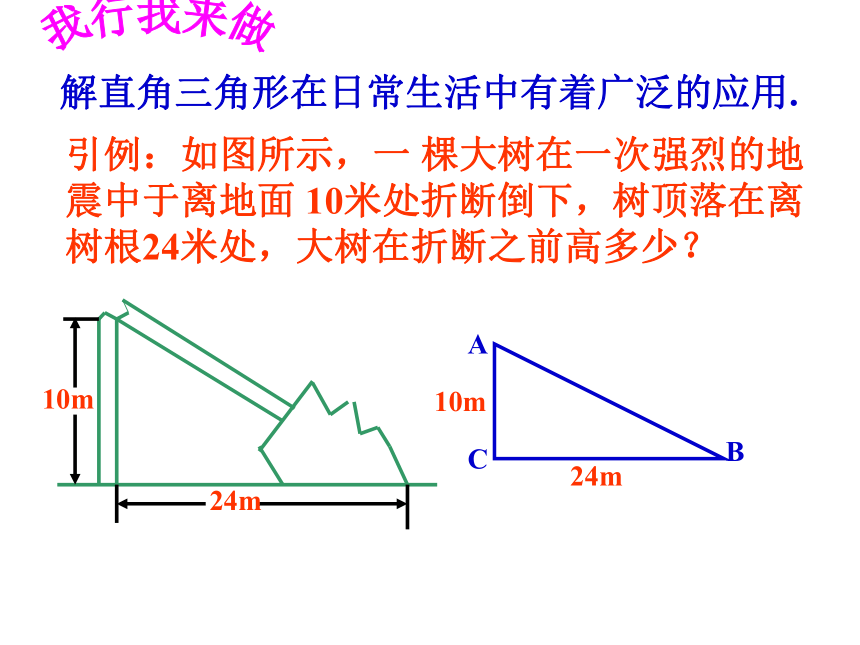
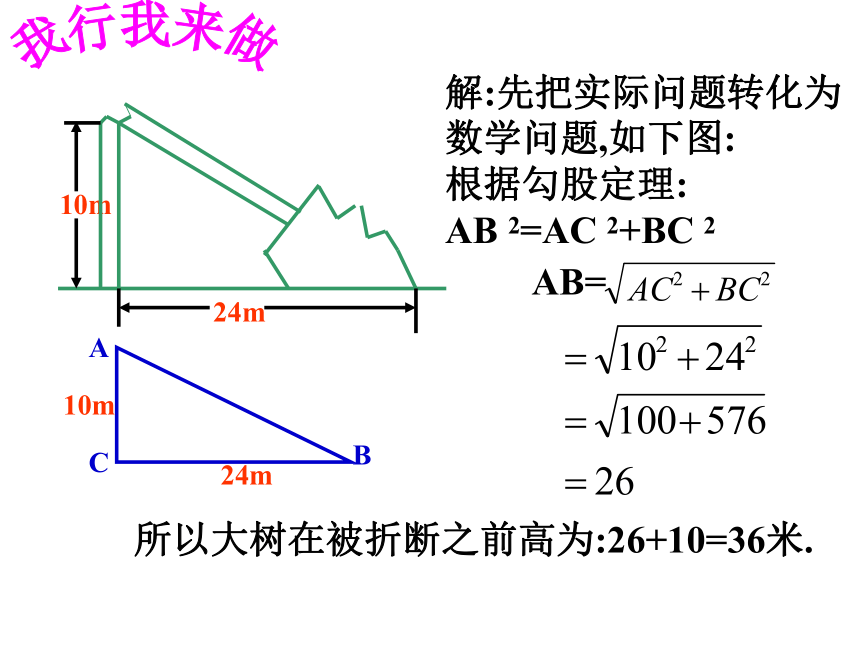
课件20张PPT。解直角三角形宜川附校 茅伟浩我行我来做解直角三角形在日常生活中有着广泛的应用.引例:如图所示,一 棵大树在一次强烈的地震中于离地面 10米处折断倒下,树顶落在离树根24米处,大树在折断之前高多少? 10m我行我来做解:先把实际问题转化为数学问题,如下图:
根据勾股定理:
AB 2=AC 2+BC 2
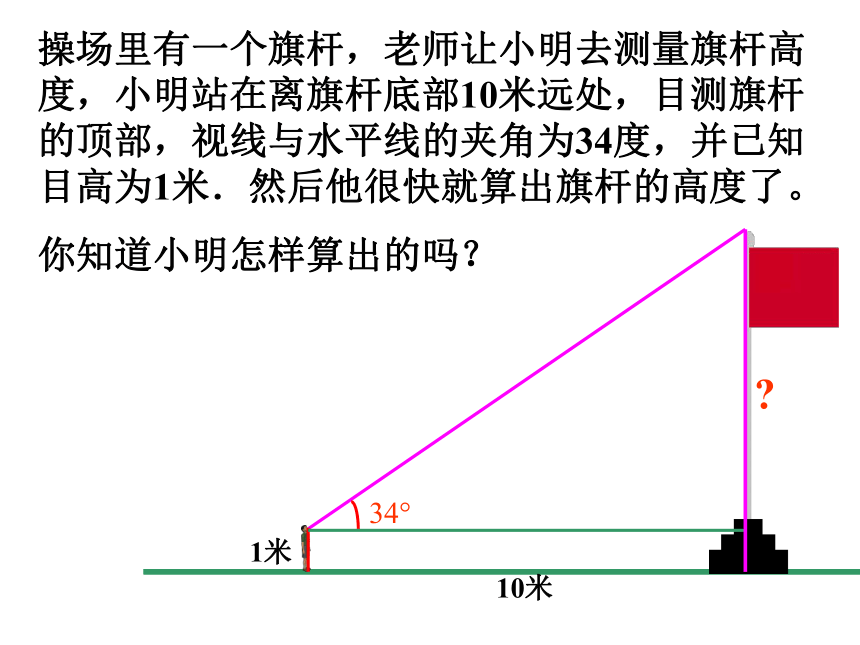
所以大树在被折断之前高为:26+10=36米.AB=操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。
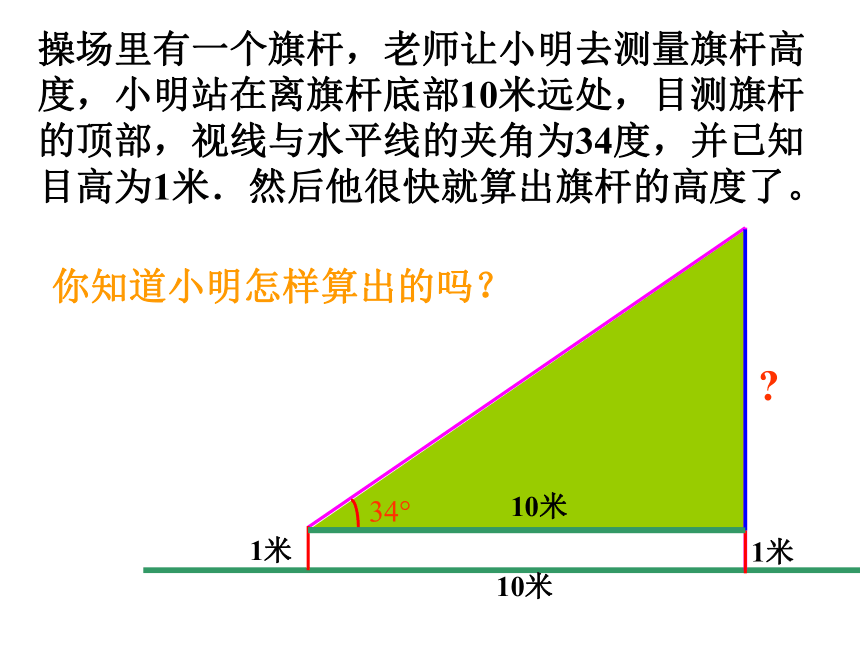
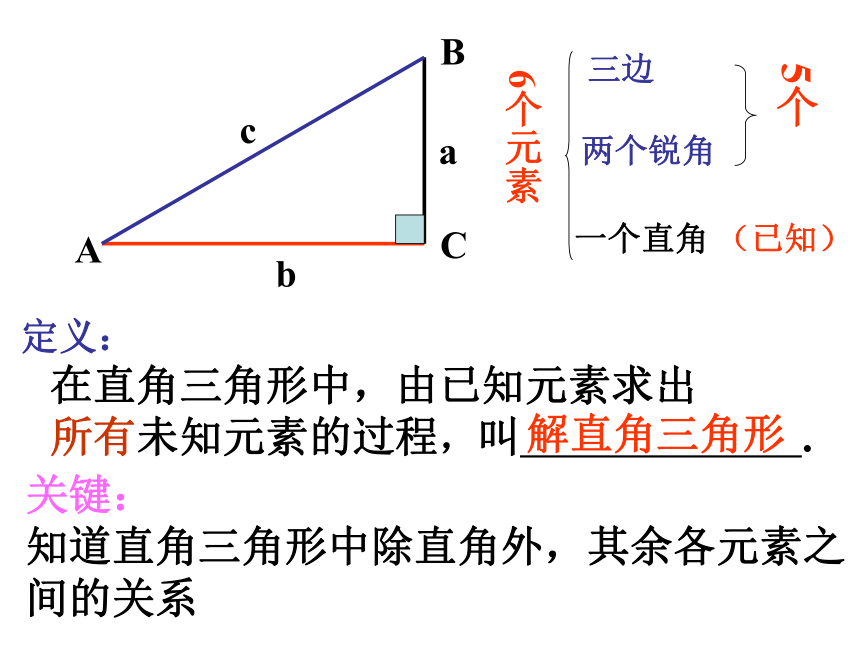
你知道小明怎样算出的吗?10米1米?1米10米?操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。你知道小明怎样算出的吗?ABC6个元素三边两个锐角一个直角(已知)5个 定义:
在直角三角形中,由已知元素求出
所有未知元素的过程,叫 . 解直角三角形abc关键:
知道直角三角形中除直角外,其余各元素之间的关系
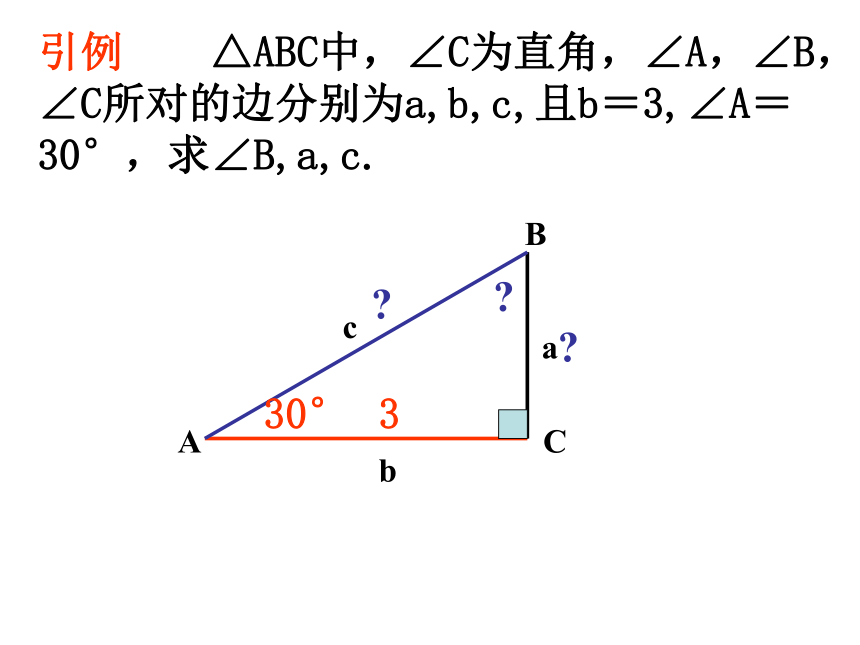
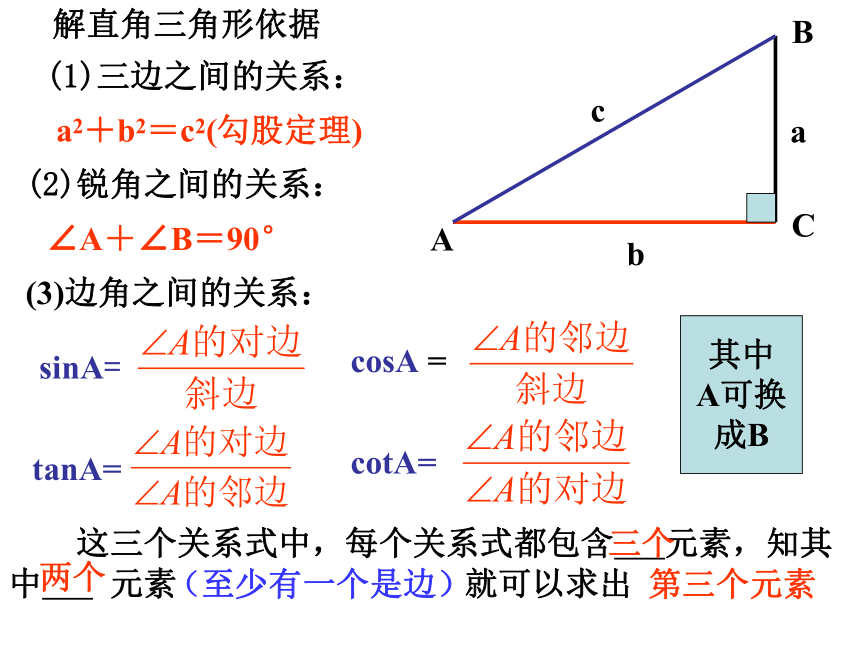
引例 △ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.ABCabc330°???解直角三角形依据 ??? (1)三边之间的关系:
???????BCabcA(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=cotA=其中
A可换
成B 这三个关系式中,每个关系式都包含 元素,知其中 元素 就可以求出 三个两个第三个元素(至少有一个是边)引例 △ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.ABCabc330°??? 1.未知元素是∠B,a,c;???? ?2.∠B最容易求,∠B=90°-∠A? 4. 由 ,可以求c分析??例2 在△ABC中,∠C=90°,c=2,∠B=30°,解这个直角三角形 .ABCabc230°?????? 例3 在△ABC中,∠C=90°, ,
,求∠A、∠B、c边. ABCabc2???优选
关系
式是
关键 ??? 例4 在△ABC中,∠C=90°,b=35,c=45,(cos39°=0.7778),解直角三角形.3545???已知斜边求直边,已知直边求直边,已知两边求一边,已知两边求一角,已知锐角求锐角,已知直边求斜边,计算方法要选择,正弦余弦很方便正切余切理当然函数关系要选好;勾股定理最方便;互余关系要记好;用除还需正余弦,能用乘法不用除.优选关系式在Rt△ABC中,∠C=90°:⑴已知∠A、 c, 则a=__________;b=_________。⑵已知∠A、 b, 则a=__________;c=_________。⑶已知∠A、 a,则b=__________;c=_________。⑷已知a、b,则c=__________。⑸已知a、c,则b=__________ 。已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。已知一锐角、对边,求邻边,用锐角的余切;
求斜边,用锐角的正弦。例5 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且c=287.4,∠B=42°6′,解这个三角形. a=ccosB=287.4×0.7420≈213.3. b=csinB=287.4×0.6704≈192.7.∠A=90°-42°6′=47°54′.cos 42°6′= 0.7420sin 42°6′= 0.6704简解在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′. C30°巩固练习ACB59o5米A 5tan59o(m)
B 5 / sin59o(m)
C 5cot59o(m)
D 5 / cos59o(m) ?3.如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成59o角,求拉线AC的长为( )B直角三角形的边角关系 解直 角三角形知一边一锐角解直角三角形知两边解直角三角形知斜边一锐角解直角三角形知一直角边一锐角解直角三角形知两直角边解直角三角形知一斜边一直角边解直角三角形解直角三角形师生小结作业“课课练”29.4(1)???? 4. △ABC中,∠C=90°,
???? (1)∠A=60°,a=10 ;
???? (2)∠B=45°,c=18.ABCabcABCabc10186045
根据勾股定理:
AB 2=AC 2+BC 2
所以大树在被折断之前高为:26+10=36米.AB=操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。
你知道小明怎样算出的吗?10米1米?1米10米?操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。你知道小明怎样算出的吗?ABC6个元素三边两个锐角一个直角(已知)5个 定义:
在直角三角形中,由已知元素求出
所有未知元素的过程,叫 . 解直角三角形abc关键:
知道直角三角形中除直角外,其余各元素之间的关系
引例 △ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.ABCabc330°???解直角三角形依据 ??? (1)三边之间的关系:
???????BCabcA(2)锐角之间的关系: ? a2+b2=c2(勾股定理) ∠A+∠B=90° (3)边角之间的关系: sinA=cosA =tanA=cotA=其中
A可换
成B 这三个关系式中,每个关系式都包含 元素,知其中 元素 就可以求出 三个两个第三个元素(至少有一个是边)引例 △ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,求∠B,a,c.ABCabc330°??? 1.未知元素是∠B,a,c;???? ?2.∠B最容易求,∠B=90°-∠A? 4. 由 ,可以求c分析??例2 在△ABC中,∠C=90°,c=2,∠B=30°,解这个直角三角形 .ABCabc230°?????? 例3 在△ABC中,∠C=90°, ,
,求∠A、∠B、c边. ABCabc2???优选
关系
式是
关键 ??? 例4 在△ABC中,∠C=90°,b=35,c=45,(cos39°=0.7778),解直角三角形.3545???已知斜边求直边,已知直边求直边,已知两边求一边,已知两边求一角,已知锐角求锐角,已知直边求斜边,计算方法要选择,正弦余弦很方便正切余切理当然函数关系要选好;勾股定理最方便;互余关系要记好;用除还需正余弦,能用乘法不用除.优选关系式在Rt△ABC中,∠C=90°:⑴已知∠A、 c, 则a=__________;b=_________。⑵已知∠A、 b, 则a=__________;c=_________。⑶已知∠A、 a,则b=__________;c=_________。⑷已知a、b,则c=__________。⑸已知a、c,则b=__________ 。已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。已知一锐角、对边,求邻边,用锐角的余切;
求斜边,用锐角的正弦。例5 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且c=287.4,∠B=42°6′,解这个三角形. a=ccosB=287.4×0.7420≈213.3. b=csinB=287.4×0.6704≈192.7.∠A=90°-42°6′=47°54′.cos 42°6′= 0.7420sin 42°6′= 0.6704简解在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′. C30°巩固练习ACB59o5米A 5tan59o(m)
B 5 / sin59o(m)
C 5cot59o(m)
D 5 / cos59o(m) ?3.如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成59o角,求拉线AC的长为( )B直角三角形的边角关系 解直 角三角形知一边一锐角解直角三角形知两边解直角三角形知斜边一锐角解直角三角形知一直角边一锐角解直角三角形知两直角边解直角三角形知一斜边一直角边解直角三角形解直角三角形师生小结作业“课课练”29.4(1)???? 4. △ABC中,∠C=90°,
???? (1)∠A=60°,a=10 ;
???? (2)∠B=45°,c=18.ABCabcABCabc10186045
