圆中典型例题(总复习)[下学期]
图片预览

文档简介
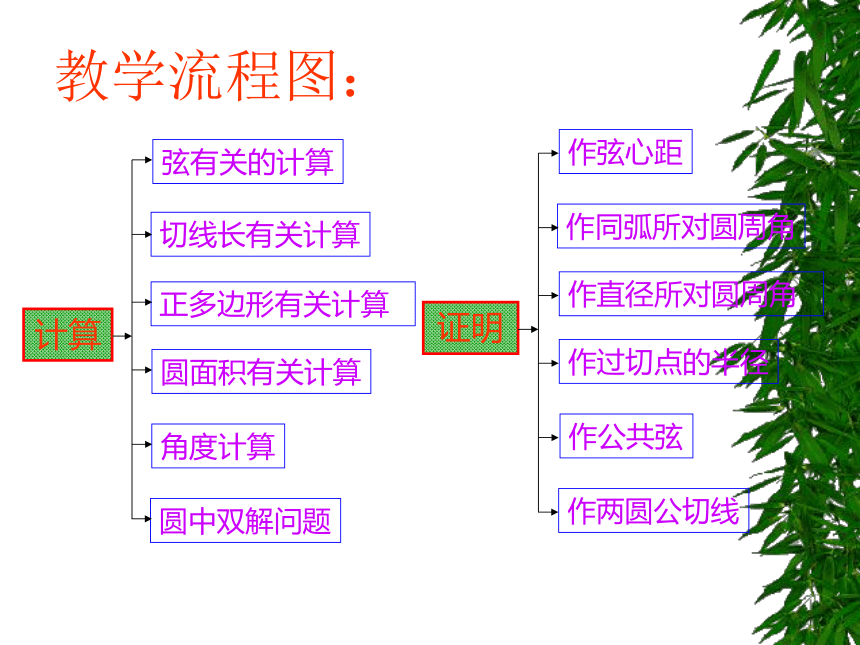
课件22张PPT。圆分类练习授课人:陈维国2003年11月教学流程图:计算弦有关的计算切线长有关计算正多边形有关计算角度计算圆面积有关计算证明圆中双解问题作弦心距作同弧所对圆周角作直径所对圆周角作公共弦作过切点的半径作两圆公切线弦有关的计算1.在直径为52cm的圆柱形油槽内装入一些油后,截面如图,如果油的最大深度为16cm,那么油面宽度AB是___cm.
2.过圆上一点引两条互相垂直的弦,如果圆心到这两条弦的距离分别是2和3,那么这两条弦长分别为_____。DCO小结:
弦长AB=a , 半径OA=r,
弦心距OD=d,弓形高CD=h
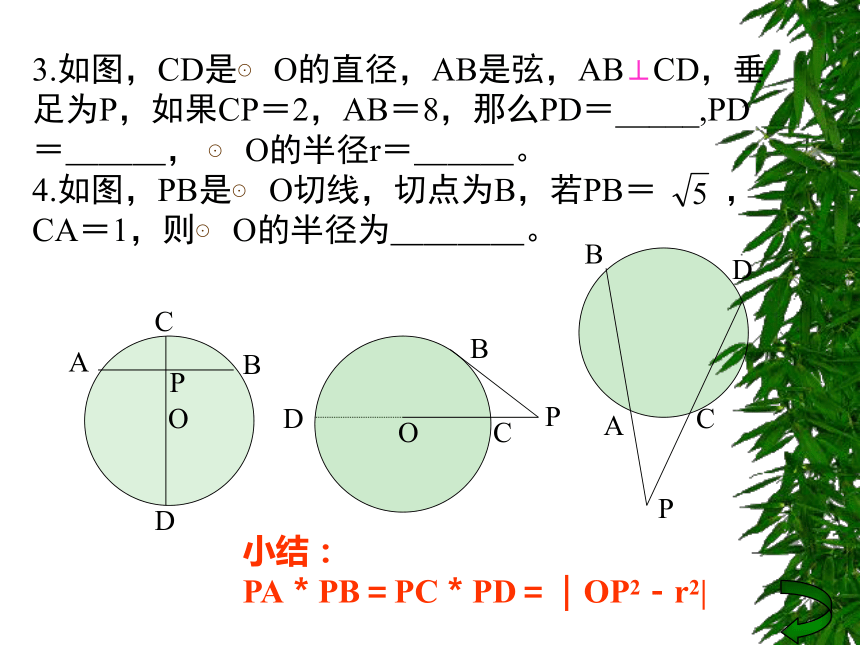
r2=a2+d2; r=d+h3.如图,CD是⊙ O的直径,AB是弦,AB⊥CD,垂足为P,如果CP=2,AB=8,那么PD=_____,PD=___, ⊙ O的半径r=___。
4.如图,PB是⊙ O切线,切点为B,若PB= ,CA=1,则⊙ O的半径为____。D小结:
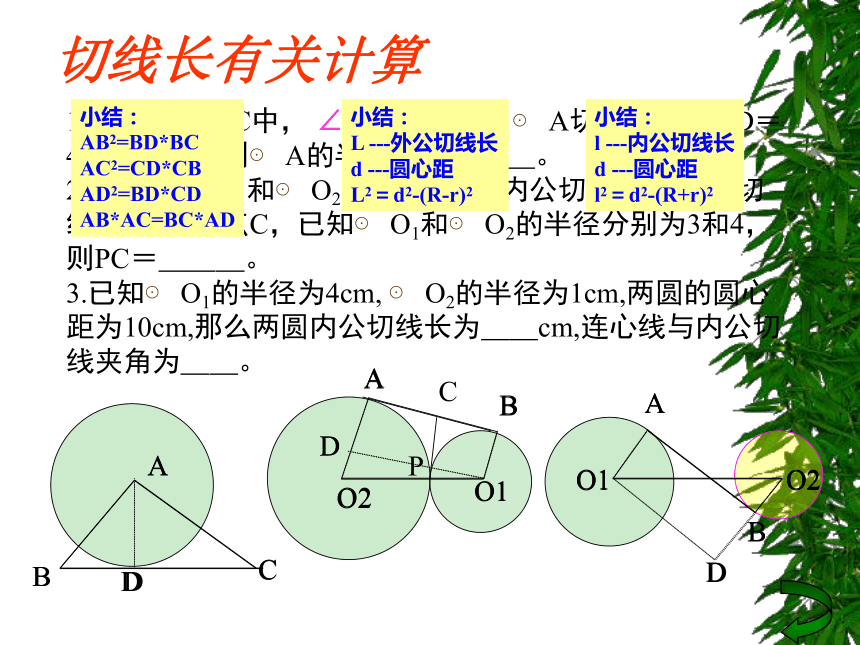
PA*PB=PC*PD=|OP2-r2|切线长有关计算1.如图,ΔABC中, ∠ BAC=900, ⊙ A切BC于D,BD=4,DC=9,则⊙ A的半径长为___。
2.如图, ⊙ O1和⊙ O2外切于点P,内公切线PC与外公切线AB相交于点C,已知⊙ O1和⊙ O2的半径分别为3和4,则PC=___。
3.已知⊙ O1的半径为4cm, ⊙ O2的半径为1cm,两圆的圆心距为10cm,那么两圆内公切线长为__cm,连心线与内公切线夹角为__。
小结:
AB2=BD*BC
AC2=CD*CB
AD2=BD*CD
AB*AC=BC*AD小结:
L ---外公切线长
d ---圆心距
L2=d2-(R-r)2小结:
l ---内公切线长
d ---圆心距
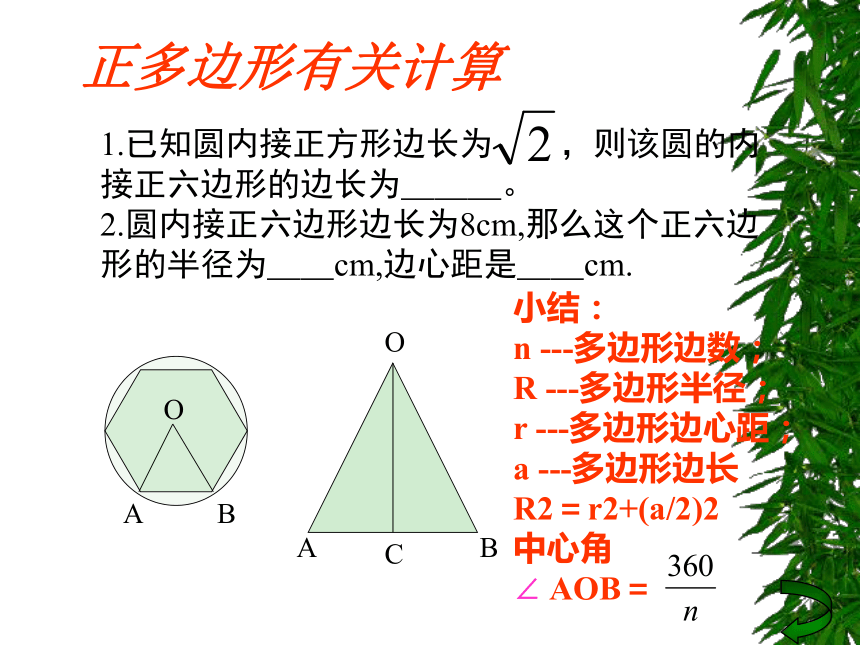
l2=d2-(R+r)2正多边形有关计算1.已知圆内接正方形边长为 ,则该圆的内
接正六边形的边长为___。
2.圆内接正六边形边长为8cm,那么这个正六边
形的半径为__cm,边心距是__cm.小结:
n ---多边形边数;
R ---多边形半径;
r ---多边形边心距;
a ---多边形边长
R2=r2+(a/2)2
中心角
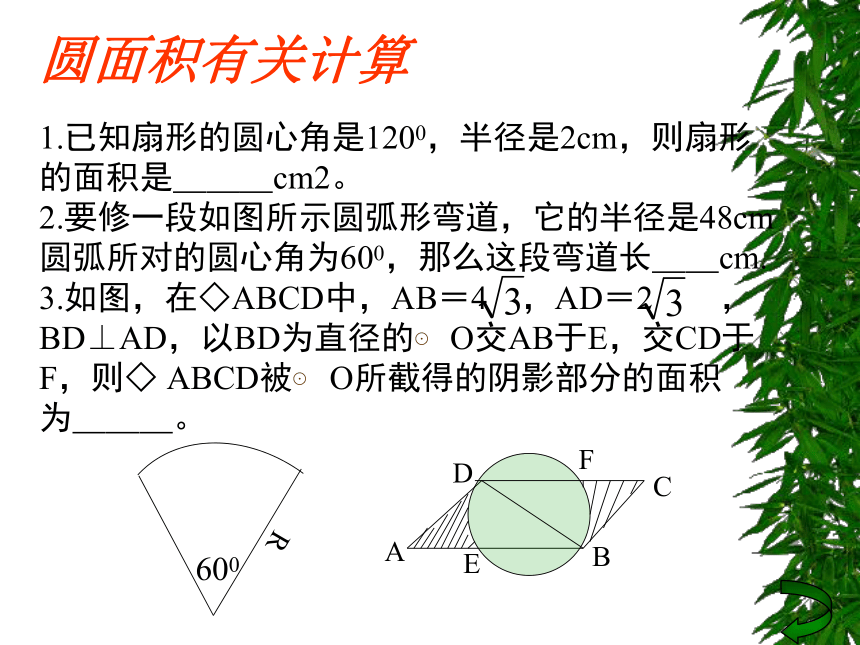
∠ AOB=圆面积有关计算1.已知扇形的圆心角是1200,半径是2cm,则扇形
的面积是___cm2。
2.要修一段如图所示圆弧形弯道,它的半径是48cm
圆弧所对的圆心角为600,那么这段弯道长__cm.
3.如图,在◇ABCD中,AB=4 ,AD=2 ,
BD⊥AD,以BD为直径的⊙ O交AB于E,交CD于
F,则◇ ABCD被⊙ O所截得的阴影部分的面积
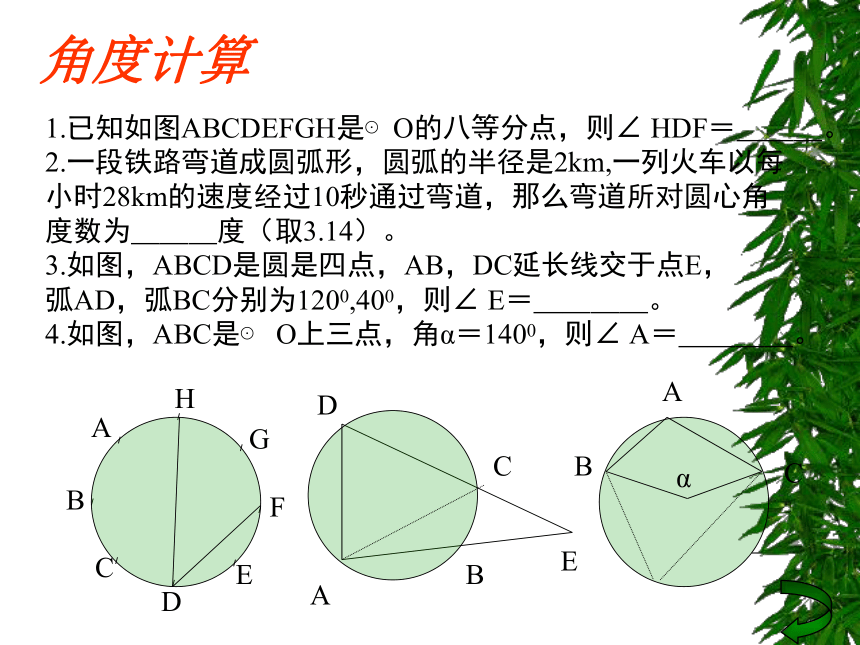
为___。 600R角度计算1.已知如图ABCDEFGH是⊙O的八等分点,则∠ HDF=___。
2.一段铁路弯道成圆弧形,圆弧的半径是2km,一列火车以每
小时28km的速度经过10秒通过弯道,那么弯道所对圆心角
度数为___度(取3.14)。
3.如图,ABCD是圆是四点,AB,DC延长线交于点E,
弧AD,弧BC分别为1200,400,则∠ E=____。
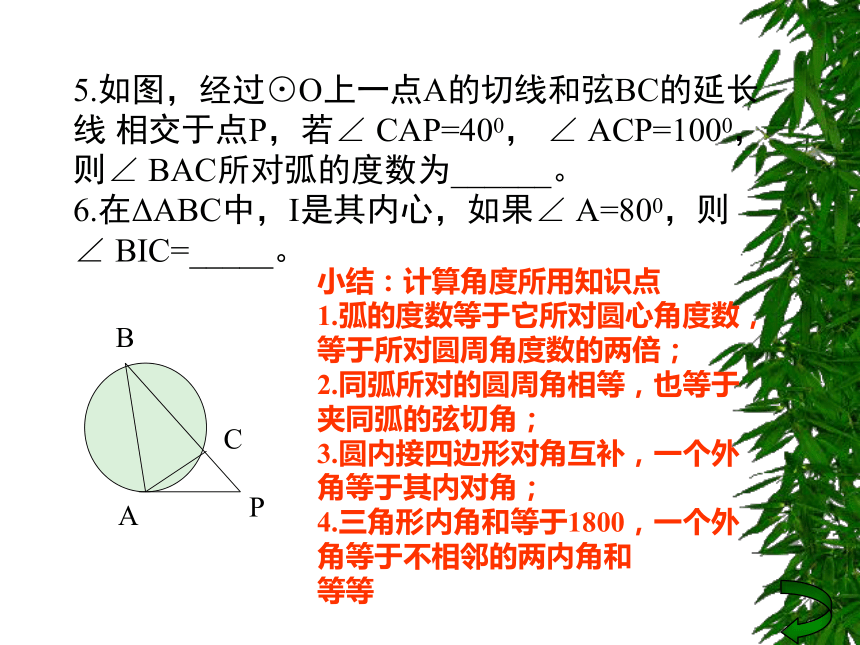
4.如图,ABC是⊙ O上三点,角α=1400,则∠ A=____。A5.如图,经过⊙O上一点A的切线和弦BC的延长线 相交于点P,若∠ CAP=400, ∠ ACP=1000,则∠ BAC所对弧的度数为______。
6.在ΔABC中,I是其内心,如果∠ A=800,则
∠ BIC=_____。小结:计算角度所用知识点
1.弧的度数等于它所对圆心角度数,
等于所对圆周角度数的两倍;
2.同弧所对的圆周角相等,也等于
夹同弧的弦切角;
3.圆内接四边形对角互补,一个外
角等于其内对角;
4.三角形内角和等于1800,一个外
角等于不相邻的两内角和
等等
1、点与圆的位置关系问题1:已知⊙O和不在⊙O上的一点P过点P的直线交 ⊙O于A、B两点PA×PB=24,OP=5,则⊙O的半径为=圆中双解问题计算2、点在直径上的有关问题2:⊙O的半径为5,AB是直径,C是圆上一点,CD⊥AB于D,且CD=4,则AD= 。3、弦与弧的位置关系3:弦长等于半径的弦所对的圆周角等于 。4、两平行弦与圆心位置问题4:⊙O直径为10cm,弦AB∥CD,AB=6cm,CD=8cm,求两弦间的距离。5、相切两圆的位置问题5:半径分别为3cm和5cm的两圆相切,则两圆圆心距为 cm6、相交两圆的公共弦问题6:⊙O1和⊙O2的半径分别为20cm和15cm,它们的公共弦AB=24cm,则它们的圆心距长为 cm.1.如图,CD是⊙ O中一条弦,两边延长CD到A,B,若AC=BD,求证∠A= ∠ B。
2.如图,EF为⊙ O的弦,EC ⊥ EF,FD ⊥ EF,分别交圆于C、D,过O点任意作一直径AB分别交CE,DF于点M、N,求证:OM=ON。作弦心距1.如图,在ΔABC中,∠A的平分线AD交BC于D,⊙ O过点A。且与BC相切于点D,与AB,AC分别相交于E、F,AD与EF相交于G,求证AF*FC=GF*DC。
2.如图,已知PA切⊙ O于点A,PBC为O的割线,E是弧BC中点,连结AE交BC于点D,求证:PA=PD。作同弧所对圆周角1.如图,以等腰ΔABC的一腰BC为直径画⊙ O,交另一腰AB于点D,交底边AC于点E,
求证∠ EDC= ∠ ECD。
2.如图,AB是⊙ O的直径,CD切⊙ O于C,BD ⊥ CD于点D,CE ⊥ AB于点E,求证:CD2=AE*EB。作直径所对圆周角1.如图, AB是⊙ O的直径,直线l切⊙ O于点E,AC ⊥ l,
BD ⊥ l,垂足分别为CD, 求证AB=AC+BD。
2.如图,AB是⊙ O的直径,EC切⊙ O于C,BE ⊥ EC于点E,交AC于点D,求证:AB=BD。作过切点的半径作公共弦1.如图, ⊙ O1和⊙ O2相交于AB两点,CD过A点分别与⊙ O1和⊙ O2相交于C、D两点, EF过B点分别与⊙ O1和⊙ O2相交于E、F两点,求证:CE ∥FD
2.如图,已知⊙ O1 和⊙ O2相交于AB两点,过B点作⊙ O1的切线交⊙ O2于点D,连结DA并延长与⊙ O1相交于C点,连结BC,过A点作AE ∥ BC,与 ⊙ O2相交于E点,与BD相交于F点, 求证:EF*BC=DE*AC D作公切线1.如图, ⊙ O1和⊙ O2外切于点P,AB是两圆的外公切线,A、B为切点,过点P的直线交⊙ O1于点C,交⊙ O2于点D,分别延长CA,DB相交于点 E,求证:CE ⊥FD
2.如图,两圆内切线于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D,求证∠APD= ∠ BPD再见策划制作:轻风拂面 2004年11月个人主页:http://chenwg7405.icpcn.com
2.过圆上一点引两条互相垂直的弦,如果圆心到这两条弦的距离分别是2和3,那么这两条弦长分别为_____。DCO小结:
弦长AB=a , 半径OA=r,
弦心距OD=d,弓形高CD=h
r2=a2+d2; r=d+h3.如图,CD是⊙ O的直径,AB是弦,AB⊥CD,垂足为P,如果CP=2,AB=8,那么PD=_____,PD=___, ⊙ O的半径r=___。
4.如图,PB是⊙ O切线,切点为B,若PB= ,CA=1,则⊙ O的半径为____。D小结:
PA*PB=PC*PD=|OP2-r2|切线长有关计算1.如图,ΔABC中, ∠ BAC=900, ⊙ A切BC于D,BD=4,DC=9,则⊙ A的半径长为___。
2.如图, ⊙ O1和⊙ O2外切于点P,内公切线PC与外公切线AB相交于点C,已知⊙ O1和⊙ O2的半径分别为3和4,则PC=___。
3.已知⊙ O1的半径为4cm, ⊙ O2的半径为1cm,两圆的圆心距为10cm,那么两圆内公切线长为__cm,连心线与内公切线夹角为__。
小结:
AB2=BD*BC
AC2=CD*CB
AD2=BD*CD
AB*AC=BC*AD小结:
L ---外公切线长
d ---圆心距
L2=d2-(R-r)2小结:
l ---内公切线长
d ---圆心距
l2=d2-(R+r)2正多边形有关计算1.已知圆内接正方形边长为 ,则该圆的内
接正六边形的边长为___。
2.圆内接正六边形边长为8cm,那么这个正六边
形的半径为__cm,边心距是__cm.小结:
n ---多边形边数;
R ---多边形半径;
r ---多边形边心距;
a ---多边形边长
R2=r2+(a/2)2
中心角
∠ AOB=圆面积有关计算1.已知扇形的圆心角是1200,半径是2cm,则扇形
的面积是___cm2。
2.要修一段如图所示圆弧形弯道,它的半径是48cm
圆弧所对的圆心角为600,那么这段弯道长__cm.
3.如图,在◇ABCD中,AB=4 ,AD=2 ,
BD⊥AD,以BD为直径的⊙ O交AB于E,交CD于
F,则◇ ABCD被⊙ O所截得的阴影部分的面积
为___。 600R角度计算1.已知如图ABCDEFGH是⊙O的八等分点,则∠ HDF=___。
2.一段铁路弯道成圆弧形,圆弧的半径是2km,一列火车以每
小时28km的速度经过10秒通过弯道,那么弯道所对圆心角
度数为___度(取3.14)。
3.如图,ABCD是圆是四点,AB,DC延长线交于点E,
弧AD,弧BC分别为1200,400,则∠ E=____。
4.如图,ABC是⊙ O上三点,角α=1400,则∠ A=____。A5.如图,经过⊙O上一点A的切线和弦BC的延长线 相交于点P,若∠ CAP=400, ∠ ACP=1000,则∠ BAC所对弧的度数为______。
6.在ΔABC中,I是其内心,如果∠ A=800,则
∠ BIC=_____。小结:计算角度所用知识点
1.弧的度数等于它所对圆心角度数,
等于所对圆周角度数的两倍;
2.同弧所对的圆周角相等,也等于
夹同弧的弦切角;
3.圆内接四边形对角互补,一个外
角等于其内对角;
4.三角形内角和等于1800,一个外
角等于不相邻的两内角和
等等
1、点与圆的位置关系问题1:已知⊙O和不在⊙O上的一点P过点P的直线交 ⊙O于A、B两点PA×PB=24,OP=5,则⊙O的半径为=圆中双解问题计算2、点在直径上的有关问题2:⊙O的半径为5,AB是直径,C是圆上一点,CD⊥AB于D,且CD=4,则AD= 。3、弦与弧的位置关系3:弦长等于半径的弦所对的圆周角等于 。4、两平行弦与圆心位置问题4:⊙O直径为10cm,弦AB∥CD,AB=6cm,CD=8cm,求两弦间的距离。5、相切两圆的位置问题5:半径分别为3cm和5cm的两圆相切,则两圆圆心距为 cm6、相交两圆的公共弦问题6:⊙O1和⊙O2的半径分别为20cm和15cm,它们的公共弦AB=24cm,则它们的圆心距长为 cm.1.如图,CD是⊙ O中一条弦,两边延长CD到A,B,若AC=BD,求证∠A= ∠ B。
2.如图,EF为⊙ O的弦,EC ⊥ EF,FD ⊥ EF,分别交圆于C、D,过O点任意作一直径AB分别交CE,DF于点M、N,求证:OM=ON。作弦心距1.如图,在ΔABC中,∠A的平分线AD交BC于D,⊙ O过点A。且与BC相切于点D,与AB,AC分别相交于E、F,AD与EF相交于G,求证AF*FC=GF*DC。
2.如图,已知PA切⊙ O于点A,PBC为O的割线,E是弧BC中点,连结AE交BC于点D,求证:PA=PD。作同弧所对圆周角1.如图,以等腰ΔABC的一腰BC为直径画⊙ O,交另一腰AB于点D,交底边AC于点E,
求证∠ EDC= ∠ ECD。
2.如图,AB是⊙ O的直径,CD切⊙ O于C,BD ⊥ CD于点D,CE ⊥ AB于点E,求证:CD2=AE*EB。作直径所对圆周角1.如图, AB是⊙ O的直径,直线l切⊙ O于点E,AC ⊥ l,
BD ⊥ l,垂足分别为CD, 求证AB=AC+BD。
2.如图,AB是⊙ O的直径,EC切⊙ O于C,BE ⊥ EC于点E,交AC于点D,求证:AB=BD。作过切点的半径作公共弦1.如图, ⊙ O1和⊙ O2相交于AB两点,CD过A点分别与⊙ O1和⊙ O2相交于C、D两点, EF过B点分别与⊙ O1和⊙ O2相交于E、F两点,求证:CE ∥FD
2.如图,已知⊙ O1 和⊙ O2相交于AB两点,过B点作⊙ O1的切线交⊙ O2于点D,连结DA并延长与⊙ O1相交于C点,连结BC,过A点作AE ∥ BC,与 ⊙ O2相交于E点,与BD相交于F点, 求证:EF*BC=DE*AC D作公切线1.如图, ⊙ O1和⊙ O2外切于点P,AB是两圆的外公切线,A、B为切点,过点P的直线交⊙ O1于点C,交⊙ O2于点D,分别延长CA,DB相交于点 E,求证:CE ⊥FD
2.如图,两圆内切线于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D,求证∠APD= ∠ BPD再见策划制作:轻风拂面 2004年11月个人主页:http://chenwg7405.icpcn.com
