等腰三角形专题检测题（附答案）

等腰三角形专题检测题
一. 选择题：（每题3分，共36分）
1. 等腰三角形的一个角是94°，则腰与底边上的高的夹角为（ ）
A. 43° B. 53° C. 47° D. 90°
2. 等腰三角形周长为13cm，其中一边长为3cm，则该等腰三角形底边长（ ）
A. 7cm B. 3cm C. 7cm或3cm D. 5cm
3. 等腰三角形的两个内角的比是1：2，则这个等腰三角形是（ ）
A. 锐角三角形 B. 直角三角形
C. 锐角三角形或直角三角形 D. 以上结论都不对
4. 已知等腰三角形的一个外角等于70°，则底角的度数为（ ）
A. 110° B. 55° C. 35° D. 不能确定
5. 等腰三角形一腰上的高与底边所成角为36°，这个等腰三角形的顶角为（ ）
A. 36° B. 72° C. 36°或72° D. 54°
6.如图，等边三角形 ( http: / / www.21cnjy.com )的边长为3，点 ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )边上一点，且 ( http: / / www.21cnjy.com )，点 ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )边上一点，若 ( http: / / www.21cnjy.com )，则 ( http: / / www.21cnjy.com )的长为( ).
A． ( http: / / www.21cnjy.com )　 　B． ( http: / / www.21cnjy.com ) 　　C． ( http: / / www.21cnjy.com )　 　D．1
HYPERLINK "http://www.21cnjy.com"
第6题图 第8题图
7.等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（ ）
A.16 B.18 C. 20 D. 16或20
8.如图，等腰△ABC中，AB=AC，P ( http: / / www.21cnjy.com )为其底角平分线的交点，将△BCP沿CP折叠，使B点恰好落在AC边上的点D处，若DA=DP，则∠A的度数为( ).
A.20° B.30° C.32° D.36°
9.等腰三角形（不等边）的角平分线、中线和高的条数总和是（ ）
A．3　　　　B．5　　　　C．7　　　　D．9
10．△ABC中，AB=AC，AB边的中垂线与直线AC所成的角为50°，则∠B等于（ ）
A．70°　　　　　　　B．20°或70° C．40°或70°　　　 D．40°或20°
11．如图在∠GAH的两边上， AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）
A．80° B．90° C．100° D．108°
12.如图所示，在下列三角形中，若AB=AC，则能被一条直线分成两
个小等腰三角形的是（ ）A．⑴⑵⑶　B．⑴⑵⑷C．⑵⑶⑷D．⑴⑶⑷
二. 填空题：（每题3分，共27分）
13. 如果等腰三角形一个角是45°，那么另外两个角的度数为
14. 等腰三角形一个外角等于110°，则底角的度数是
15. 等腰三角形 互相重合
16. 等腰三角形底边长为10，则其腰长x的范围是
17. 等腰三角形的底边长为5，一腰上中线把这个三角形周长分为两部分，它们的差为3，则腰长为
18.如图， ( http: / / www.21cnjy.com )为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则四个结论正确的是 ．（把所有正确答案的序号都填写在横线上）①AP平分∠BAC；②AS=AR；③QP∥AR；④ ( http: / / www.21cnjy.com )≌△QSP．
( http: / / www.21cnjy.com )
19.如上图所示，在直角△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，若CD＝4，则点D到斜边AB的距离为 .
20.等腰三角形一腰上的中线为把周长分为6和9两部分，则该等腰三角形腰长为 。
21.等腰三角形两内角的度数之比是1：2，则顶角的度数为_______________________
三. 解答题：（共41分）
22. (6分)如图，已知AB=AE，∠B=∠E，BC=ED，F是CD中点，求证：AF⊥CD
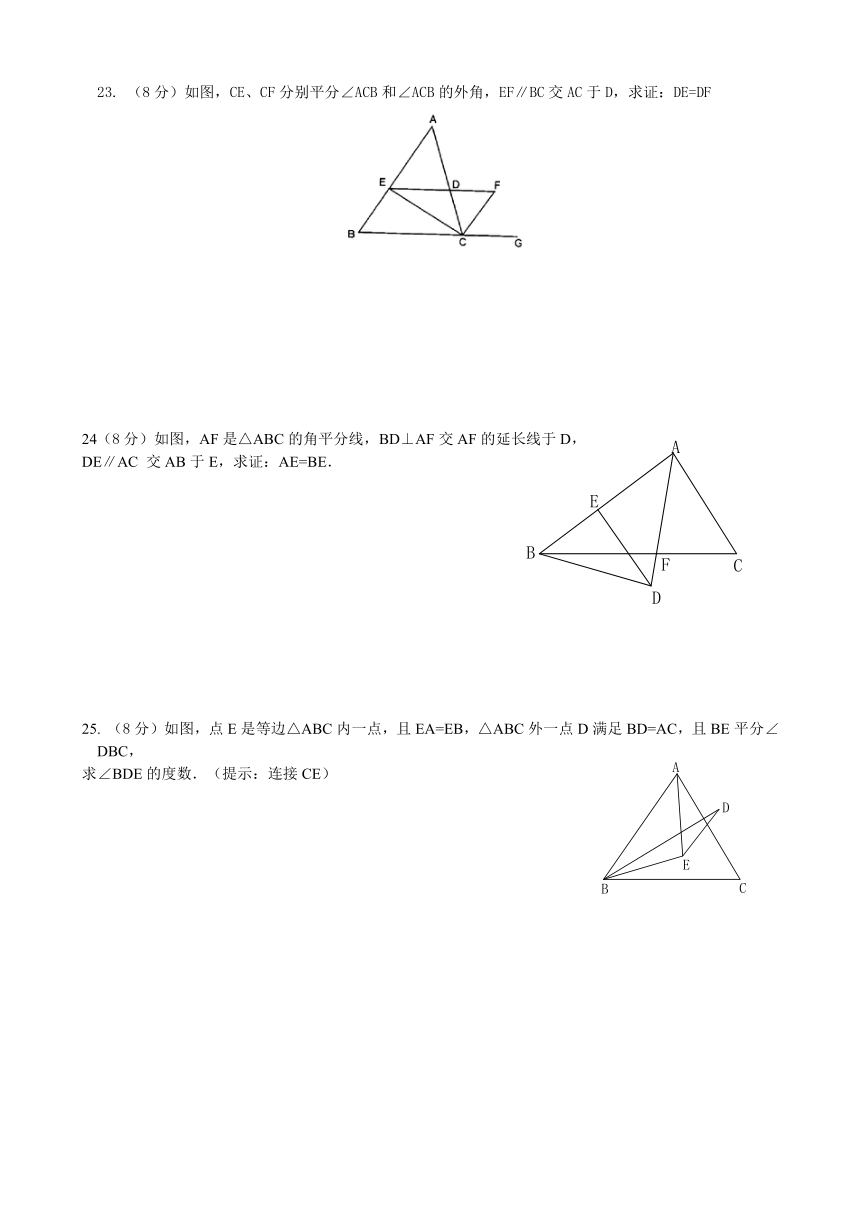
23. （8分）如图，CE、CF分别平分∠ACB和∠ACB的外角，EF∥BC交AC于D，求证：DE=DF
( http: / / www.21cnjy.com )
24（8分）如图，AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，
DE∥AC交AB于E，求证：AE=BE．
25. （8分）如图，点E是等边△ABC内一点，且EA=EB，△ABC外一点D满足BD=AC，且BE平分∠DBC，
求∠BDE的度数．（提示：连接CE）
26（11分）（1）如图1，△ABC和△CDE都是等边三角形，且B、C、D三点共线，联结AD、BE
相交于点P，求证： BE = AD.
（2）如图2，在△BCD中，∠BCD＜12 ( http: / / www.21cnjy.com )0°，分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF，联结AD、BE和CF交于点P，下列结论中正确的是 ___________________________（只填序号即可）
①AD=BE=CF；②∠BEC=∠ADC；③∠DPE=∠EPC=∠CPA=60°；
（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE.
【试题答案】
一.
1——5 C B C C B 6——8 B C D 9——12CCDD
二.
13. 45°和90°或67.5°和67.5°
14. 70°或55°
15. 顶角角平分线和底边中线和底边高线
16. 大于5
17. 8
18.①②③④
19.4
20.6或4
21.36°或90°
三.
22. 连结AC和AD，证明△ABC≌△AED，得到AC=AD，再利用等腰三角形三线合一
23. 分别证明DE=DC，DF=DC，所以DE=DF
24.证明：DE‖AC，∠EDA=∠CAD ( http: / / www.21cnjy.com )；
AF平分∠CAB，∠EAD=∠CAD。∠EAD=∠EDA，AE=DE
AD⊥BD，∠EDA+∠EDB=90°，∠EAD+∠EBD=90。
∠EBD=∠EDB，BE=DE。
所以AE=BE
25.解：连接CE，
∵A ( http: / / www.21cnjy.com )C=BC，AE=BE，CE为公共边，
∴△BCE≌△ACE，
∴∠BCE=∠ACE=30°
又BD=AC=BC，∠DBE=∠CBE，BE为公共边，
∴△BDE≌△BCE，
∴∠BDE=∠BCE=30°
26.(1)证明：∵△ABC和△CDE都是等边三角形
∴BC=AC，CE=CD，∠ACB=∠DCE=60°
∴∠BCE=∠ACD
∴△BCE≌△ACD（SAS）
∴BE=AD
（2）①②③都正确
（3）证明：在PE上截取PM=PC，联结CM
由（1）可知，△BCE≌△ACD（SAS）
∴∠1=∠2
设CD与BE交于点G,,在△CGE和△PGD中
∵∠1=∠2，∠CGE=∠PGD
∴∠DPG=∠ECG=60°同理∠CPE=60°
∴△CPM是等边三角形
∴CP=CM，∠PMC=60°
∴∠CPD=∠CME=120°
∵∠1=∠2,∴△CPD≌△CME（AAS）
∴PD=ME
∴BE=PB+PM+ME=PB+PC+PD.
即PB+PC+PD=BE.
第12题图
第11题图
第19题
第18题
B
A
C
D
F
E
第1题图2
第1题图1