2023年广东省佛山市南海区桂江第一初级中学九年级下学期3月份适应性调研数学试题(无答案)
文档属性
| 名称 | 2023年广东省佛山市南海区桂江第一初级中学九年级下学期3月份适应性调研数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 420.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 14:18:38 | ||
图片预览

文档简介
初三数学科三月份适应性调研试题
一、选择题(每题3分,共30分)
1.三角形在正方形网格中的位置如图所示,则的值是( )
A. B. C. D.
2.如图,矩形ABCD的,,则BD的长为( )
A. B.8 C. D.4
3.如图,∠CBE是内接四边形ABCD的一个外角,若,则∠CBE的度数是( )
A.105° B.80° C.75° D.60°
4.已知点(-2,3)在反比例函数的图象,则下列各点也在该图象上的是( )
A.(2,3 B.(1,-6) C. D.(0,0)
5·若是一元二次方程的一个根,则这个方程的另一个根是( )
A.-4 B.2 C.3 D.6
6.已知在平面直角坐标系中,P点坐标为(3,4),若以原点O为圆心,半径5cm画圆,则点P与的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.不能确定
7.已知BD是的对角线,E是AB上一点,连接EC,交BD于点F,若与的面积比是1:9,则的值为( )
A. B. C. D.
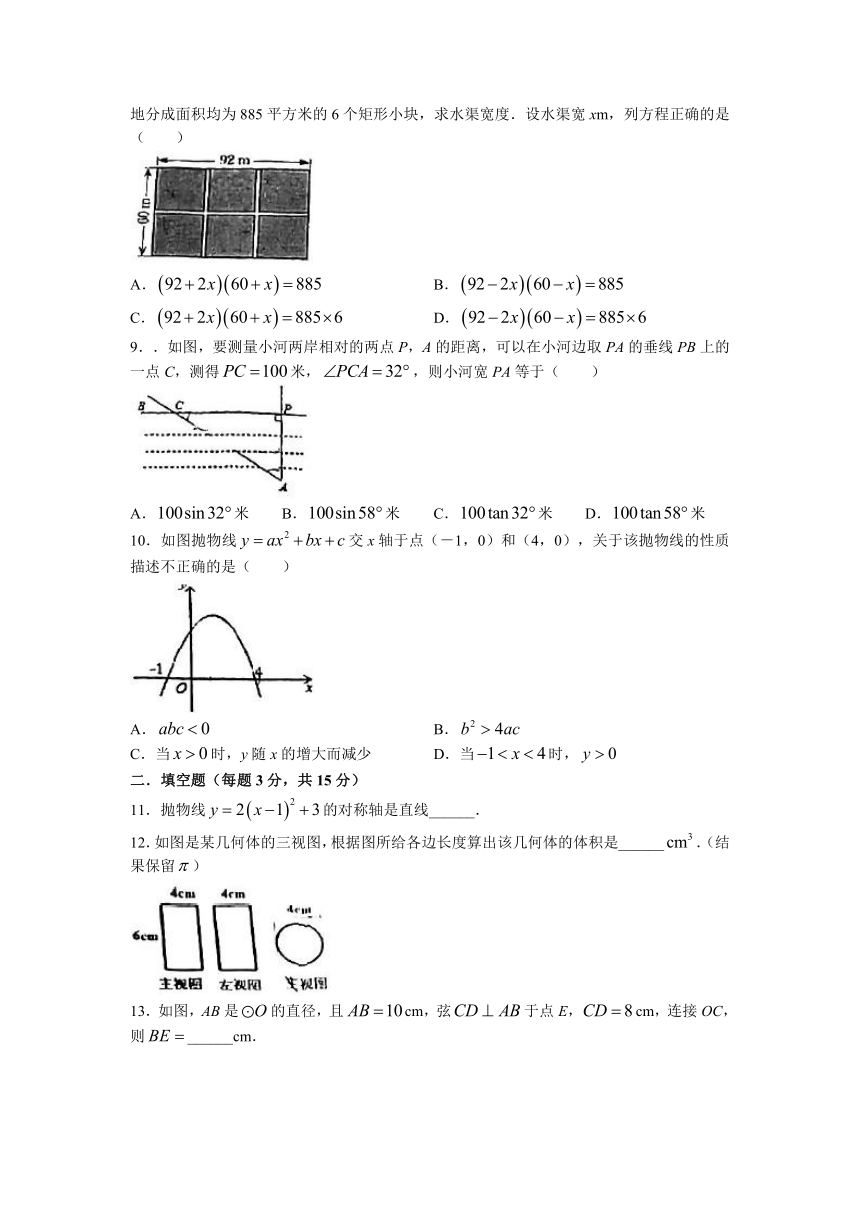
8.如图,在一块长92m,宽60m的矩形耕地上挖三条水渠(水渠的宽都相等),水渠把耕地分成面积均为885平方米的6个矩形小块,求水渠宽度.设水渠宽xm,列方程正确的是( )
A. B.
C. D.
9..如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得米,,则小河宽PA等于( )
A.米 B.米 C.米 D.米
10.如图抛物线交x轴于点(-1,0)和(4,0),关于该抛物线的性质描述不正确的是( )
A. B.
C.当时,y随x的增大而减少 D.当时,
二.填空题(每题3分,共15分)
11.抛物线的对称轴是直线______.
12.如图是某几何体的三视图,根据图所给各边长度算出该几何体的体积是______.(结果保留)
13.如图,AB是的直径,且cm,弦于点E,cm,连接OC,则______cm.
14.如图在平面直角坐如系中,O为坐标原点,点P是反比例函数的图象上的一点,等边的面积是18,则______.
15.如图,正方形ABCD的边长为a,点E在AB上运动(点E不与A,B重合),,点P在射线AM上,且,CF与AD相交于点G,连接EC,EF,EG.则下列结论中:①;②;③;④的最大值是,正确的是______(填写所有正确结论的序号).
三、解答题(每题8分,共24分)
16.计算:
17.如图,晚上,小亮站在广场上乘凉.线段AB表示站立的小亮,线段OP表示广场上灯杆,P为照明灯.
(1)画出小亮在路灯P照明下的投影,并记作BC.(3分)
(2)如果小亮身高1.6m,他站在距离灯杆OP 13m的B处时测得其影长,求灯杆OP的高度.(5分)
18.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作BD的垂线交BA的延长线于以E.
(1)证明:.(4分)
(2)若,,求菱形ABCD的面积.(4分)
四、解答题(每题9分,共27分)
19.为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数,并补全条形统计图.(2分)
(2)若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(2分)
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.(4分)
20.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
售价x(元/千克) … 20.5 24 26.5 26 …
销售量y(千克) … 39 32 27 28 …
(1)某天这种水果的售价为25元/千克,求当天该水果的销售量.(5分)
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?(4分)
21.如图,一次函数的图象与反比例函数(k为常数且)的图象交于,B两点.
(1)求此反比例函数的表达式及点B的坐标;(4分)
(2)当反比例函数值大于一次函数值时,写出x的取值范围.(1分)
(3)在y轴上存在点P,使得的周长最小,求点P的坐标及的周长.(4分)
五、解答题(每题12分,共24分)
22.如图,在中,,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是的切线;(4分)
(2)连接DF,证明:.(4分)
(3)若,,求AD的长.(4分)
23.已知抛物线与x轴有两个不同的变点.
(1)试确定c的取值范围.(2分)
(2)设该抛物线与x轴的交点为A,B,其中A(1,0);抛物线与y轴交于点C,如图所示.
①求该抛物线的表达式并确定B点坐标和C点坐标;(4分)
②连接BC,动点D以每秒1个单位长度的速度由A向B运动,同时动点E以每秒2个单位长度的速度由B向C运动,连接DE,当点E到达点C的位置时,D、E同时停止运动,设运动时间为t秒.当为直角三角形时,求的值(6分).
一、选择题(每题3分,共30分)
1.三角形在正方形网格中的位置如图所示,则的值是( )
A. B. C. D.
2.如图,矩形ABCD的,,则BD的长为( )
A. B.8 C. D.4
3.如图,∠CBE是内接四边形ABCD的一个外角,若,则∠CBE的度数是( )
A.105° B.80° C.75° D.60°
4.已知点(-2,3)在反比例函数的图象,则下列各点也在该图象上的是( )
A.(2,3 B.(1,-6) C. D.(0,0)
5·若是一元二次方程的一个根,则这个方程的另一个根是( )
A.-4 B.2 C.3 D.6
6.已知在平面直角坐标系中,P点坐标为(3,4),若以原点O为圆心,半径5cm画圆,则点P与的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.不能确定
7.已知BD是的对角线,E是AB上一点,连接EC,交BD于点F,若与的面积比是1:9,则的值为( )
A. B. C. D.
8.如图,在一块长92m,宽60m的矩形耕地上挖三条水渠(水渠的宽都相等),水渠把耕地分成面积均为885平方米的6个矩形小块,求水渠宽度.设水渠宽xm,列方程正确的是( )
A. B.
C. D.
9..如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得米,,则小河宽PA等于( )
A.米 B.米 C.米 D.米
10.如图抛物线交x轴于点(-1,0)和(4,0),关于该抛物线的性质描述不正确的是( )
A. B.
C.当时,y随x的增大而减少 D.当时,
二.填空题(每题3分,共15分)
11.抛物线的对称轴是直线______.
12.如图是某几何体的三视图,根据图所给各边长度算出该几何体的体积是______.(结果保留)
13.如图,AB是的直径,且cm,弦于点E,cm,连接OC,则______cm.
14.如图在平面直角坐如系中,O为坐标原点,点P是反比例函数的图象上的一点,等边的面积是18,则______.
15.如图,正方形ABCD的边长为a,点E在AB上运动(点E不与A,B重合),,点P在射线AM上,且,CF与AD相交于点G,连接EC,EF,EG.则下列结论中:①;②;③;④的最大值是,正确的是______(填写所有正确结论的序号).
三、解答题(每题8分,共24分)
16.计算:
17.如图,晚上,小亮站在广场上乘凉.线段AB表示站立的小亮,线段OP表示广场上灯杆,P为照明灯.
(1)画出小亮在路灯P照明下的投影,并记作BC.(3分)
(2)如果小亮身高1.6m,他站在距离灯杆OP 13m的B处时测得其影长,求灯杆OP的高度.(5分)
18.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作BD的垂线交BA的延长线于以E.
(1)证明:.(4分)
(2)若,,求菱形ABCD的面积.(4分)
四、解答题(每题9分,共27分)
19.为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数,并补全条形统计图.(2分)
(2)若本市人口300万人,估算该市对市创卫工作表示满意和非常满意的人数.(2分)
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自同区的概率.(4分)
20.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
售价x(元/千克) … 20.5 24 26.5 26 …
销售量y(千克) … 39 32 27 28 …
(1)某天这种水果的售价为25元/千克,求当天该水果的销售量.(5分)
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?(4分)
21.如图,一次函数的图象与反比例函数(k为常数且)的图象交于,B两点.
(1)求此反比例函数的表达式及点B的坐标;(4分)
(2)当反比例函数值大于一次函数值时,写出x的取值范围.(1分)
(3)在y轴上存在点P,使得的周长最小,求点P的坐标及的周长.(4分)
五、解答题(每题12分,共24分)
22.如图,在中,,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是的切线;(4分)
(2)连接DF,证明:.(4分)
(3)若,,求AD的长.(4分)
23.已知抛物线与x轴有两个不同的变点.
(1)试确定c的取值范围.(2分)
(2)设该抛物线与x轴的交点为A,B,其中A(1,0);抛物线与y轴交于点C,如图所示.
①求该抛物线的表达式并确定B点坐标和C点坐标;(4分)
②连接BC,动点D以每秒1个单位长度的速度由A向B运动,同时动点E以每秒2个单位长度的速度由B向C运动,连接DE,当点E到达点C的位置时,D、E同时停止运动,设运动时间为t秒.当为直角三角形时,求的值(6分).
同课章节目录
