三角形的中位线
图片预览


文档简介
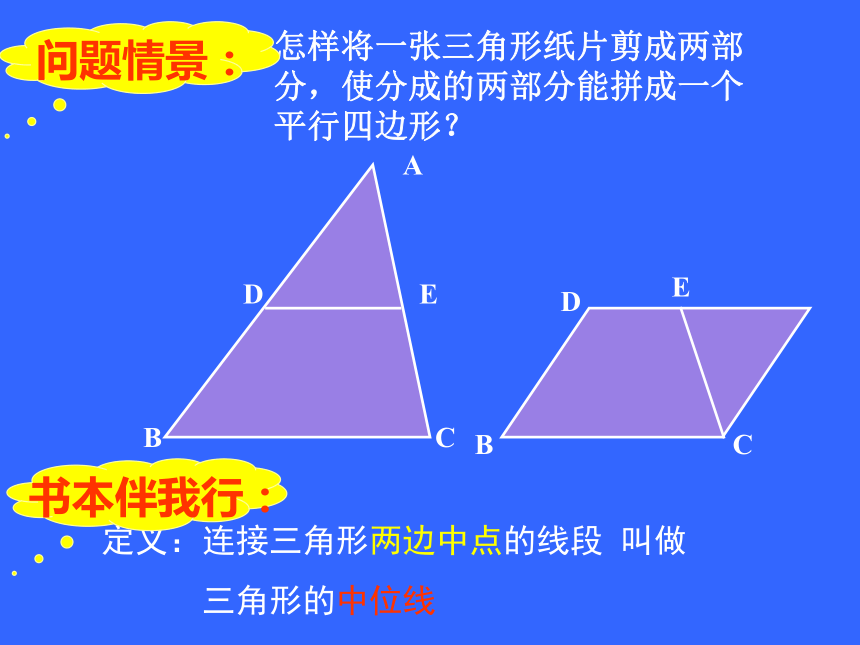
课件12张PPT。三角形的中位线ABCDE怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?定义:连接三角形两边中点的线段 叫做
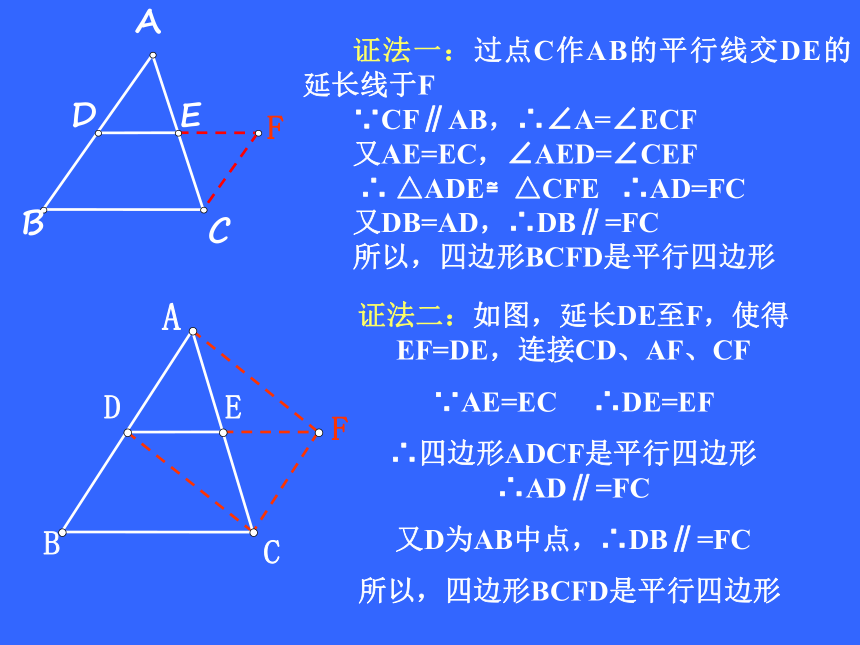
三角形的中位线证法一:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴ △ADE≌△CFE ∴AD=FC
又DB=AD,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法二:如图,延长DE至F,使得EF=DE,连接CD、AF、CF
∵AE=EC ∴DE=EF
∴四边形ADCF是平行四边形∴AD∥=FC
又D为AB中点,∴DB∥=FC
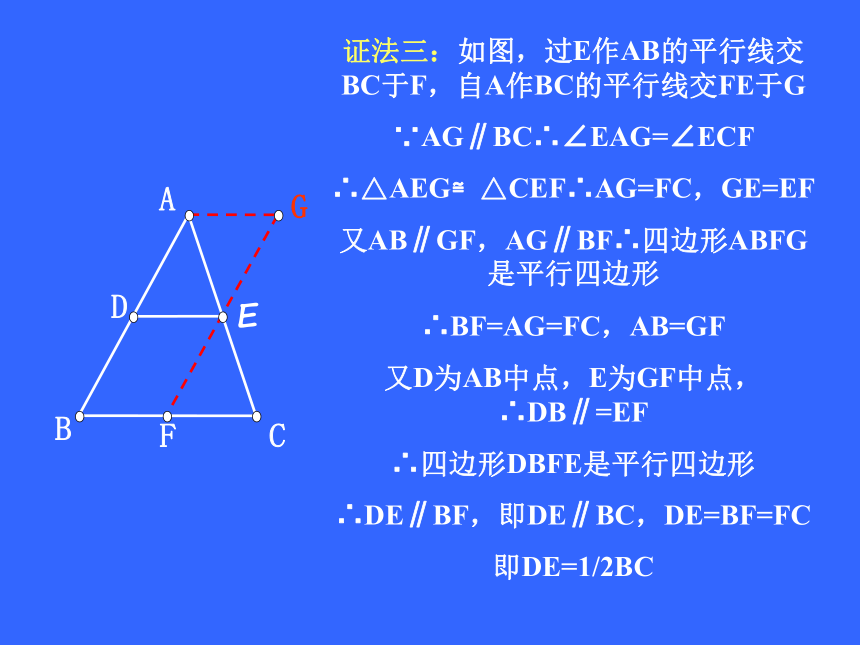
所以,四边形BCFD是平行四边形?ABCEDFABCEDF证法三:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BCABCEDFG三角形中位线定理ABCDE 三角形的中位线平行于第三边,并且等于它的一半。几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)
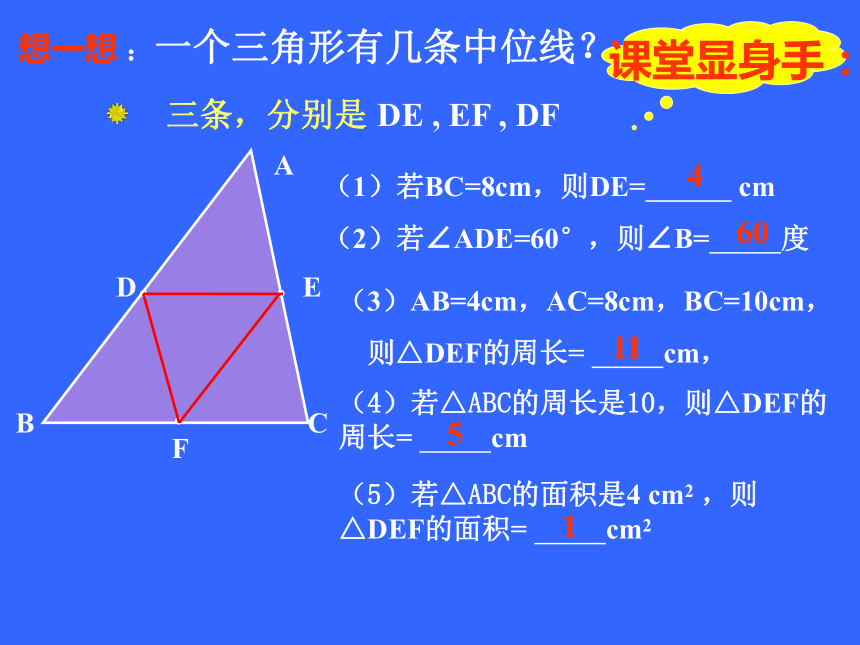
∴DE∥BC,且DE= BC(三角形的中位线平行于第三边,并且等于它的一半) 三条,分别是 DE , EF , DFABCD。。E。F想一想 :一个三角形有几条中位线? (1)若BC=8cm,则DE= cm
(2)若∠ADE=60°,则∠B= 度(3)AB=4cm,AC=8cm,BC=10cm,
则△DEF的周长= cm,
(4)若△ABC的周长是10,则△DEF的周长= cm(5)若△ABC的面积是4 cm2 ,则△DEF的面积= cm24601151⑶已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——, 面积为△ABC面积的——,⑵已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。∠B —— ∠HPN(填“=”或“≠”)=ABCDEF已知:△ABC中,AB=AC,D、E、F分别是AB、AC、BC的中点。
求证:四边形ADFE是菱形。例题猜想:四边形EFGH是什么四边形已知:在任意四边形ABCD中,E.F.G.H分别是
AB、BC、CD、DA的中点.O如图,A、B两点被池塘隔开,
如何才能知道它们之间的距离呢?在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?答:A、B两点的距离是40m。∵MN是△ABC的中位线,∴MN= AB (三角形中位线定理) ∴AB=2MN=40m.3.已知:如图 E、F把四边形ABCD的对角线BD三等分,CE、CF的延长线分别平分AB、AD
求证:四边形ABCD是平行四边形 2.已知:如图 E、F分别是AC、BD的中点,CD≧ AB,
CD与AB不平行。
求证: EF> 1/2(CD- AB).G小结: 连结三角形两边中点的线段叫做三角形的中位线。三角形中位线定理: 三角形的中位线平行于第三边,并且等于它的一半。① 证明平行问题用 途② 证明一条线段是另一条线段
的2倍或1/2
三角形的中位线证法一:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴ △ADE≌△CFE ∴AD=FC
又DB=AD,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法二:如图,延长DE至F,使得EF=DE,连接CD、AF、CF
∵AE=EC ∴DE=EF
∴四边形ADCF是平行四边形∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形?ABCEDFABCEDF证法三:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BCABCEDFG三角形中位线定理ABCDE 三角形的中位线平行于第三边,并且等于它的一半。几何语言:∵DE是△ABC的中位线(或AD=BD,AE=CE)
∴DE∥BC,且DE= BC(三角形的中位线平行于第三边,并且等于它的一半) 三条,分别是 DE , EF , DFABCD。。E。F想一想 :一个三角形有几条中位线? (1)若BC=8cm,则DE= cm
(2)若∠ADE=60°,则∠B= 度(3)AB=4cm,AC=8cm,BC=10cm,
则△DEF的周长= cm,
(4)若△ABC的周长是10,则△DEF的周长= cm(5)若△ABC的面积是4 cm2 ,则△DEF的面积= cm24601151⑶已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——, 面积为△ABC面积的——,⑵已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。∠B —— ∠HPN(填“=”或“≠”)=ABCDEF已知:△ABC中,AB=AC,D、E、F分别是AB、AC、BC的中点。
求证:四边形ADFE是菱形。例题猜想:四边形EFGH是什么四边形已知:在任意四边形ABCD中,E.F.G.H分别是
AB、BC、CD、DA的中点.O如图,A、B两点被池塘隔开,
如何才能知道它们之间的距离呢?在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?答:A、B两点的距离是40m。∵MN是△ABC的中位线,∴MN= AB (三角形中位线定理) ∴AB=2MN=40m.3.已知:如图 E、F把四边形ABCD的对角线BD三等分,CE、CF的延长线分别平分AB、AD
求证:四边形ABCD是平行四边形 2.已知:如图 E、F分别是AC、BD的中点,CD≧ AB,
CD与AB不平行。
求证: EF> 1/2(CD- AB).G小结: 连结三角形两边中点的线段叫做三角形的中位线。三角形中位线定理: 三角形的中位线平行于第三边,并且等于它的一半。① 证明平行问题用 途② 证明一条线段是另一条线段
的2倍或1/2
