第四单元_第11课时_ 最小公倍数的应用(教学课件)-五年级数学下册人教版(共26张PPT)
文档属性
| 名称 | 第四单元_第11课时_ 最小公倍数的应用(教学课件)-五年级数学下册人教版(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
小学数学·五年级(下)·RJ
第11课时 最小公倍数的
应用
能够将生活中的实际问题转化为数学问题,提高解决问题的能力。
通过实际运用,进一步理解公倍数的意义,并能运用公倍数解决简单问题。
在参与中,体验学习和探索的乐趣,增强对数学学习的兴趣,获得成功体验。
能熟练地将生活中实际问题转化为求公倍数的问题。
知道问题中出现“最小”、“至少”等类似字眼时,运用“最小公倍数”来解决问题。
通过对信息和问题的分析,培养学生发现问题和解决问题的意识,培养推理能力。
在生活中,你见过贴瓷砖现象吗?
想一想:施工师傅在贴瓷砖之前需要进行哪些计算?
6的倍数有( )。
9的倍数有( )。
6和9的公倍数有( )。
6,12,18,24,30,36,···
9,18,27,36,45,54,···
18,36,···
求6和9的公倍数有哪些?
阅读习题,理解题意。
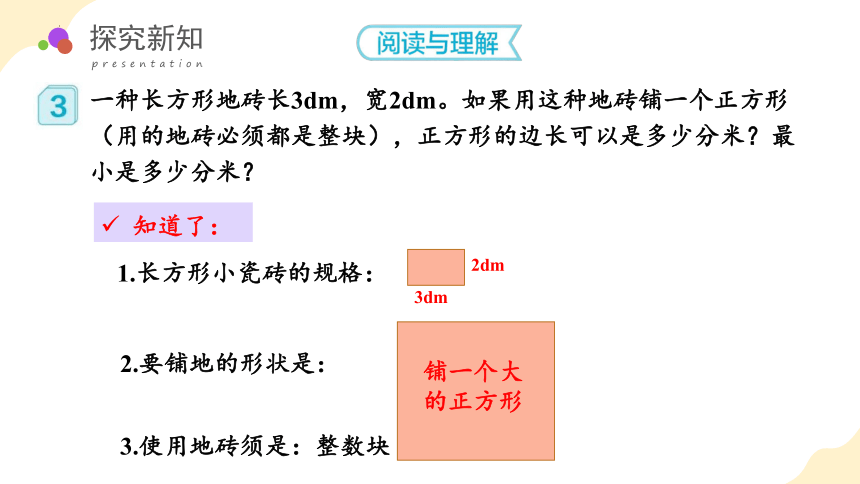
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
阅读习题你知道了哪些信息?
要求的问题是什么?
有哪些特殊要求?
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
1.长方形小瓷砖的规格:
知道了:
2dm
3dm
铺一个大的正方形
3.使用地砖须是:整数块
2.要铺地的形状是:
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
要解决的问题:
dm
用整块数长方形地砖铺成一个大正方形
2dm
3dm
正方形地面的边长可以是多少分米?
正方形地面的边长最小是多少分米?
运用公倍数的知识解决问题
要用整块的这种长方形墙砖铺出一个大的正方形。
可以先画一画,拼一拼尝试一下。
3dm
2dm
?dm
?dm
拼成的大正方形的边长可以是多少呢?
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
自主探究
1. 用长3cm,宽2cm的卡片代替墙砖拼一拼。
2. 在格子图上画一画。
3. 边操作边思考:正方形的边长可以是多少分米 最小是多少分米
4. 同桌交流,说说你摆出的正方形边长是多少。
3dm
2dm
6dm
6dm
方法一:
方法二:
12dm
12dm
方法三:
边长: ?dm
拼成的大正方形的边长有什么共同点?
拼一拼,试一试:
我发现:正方形边长必须既是3的倍数,又是2的倍数。
3dm
2dm
?dm
?dm
那就是找2和3的公倍数来作为正方形地面的边长。
3的公倍数:3,6,9,12,15,18,···
2和
所以,可以铺出边长是 6dm、12dm、18dm、··· 的正方形,正方形边长最小是 6 dm。
答:正方形的边长可以是6分米、12分米、18分米、…最小是6分米。
在边长是6dm的正方形上画一画,看找得对不对。
解决这个问题的关键是把铺砖的问题转化成求公倍数的问题。
回顾与反思
达标练习,巩固成果
1.参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
40以内6和9的公倍数有18,36
答:可能是18人或36人。
(2)两个连续自然数的和是13,这两个数的最大公因数是( ),最小公倍数是( )。
(1)15和45的最大公因数是( ),最小公倍数是( )。
2. 填一填。
(3)如果a÷b=4(a、b为非0自然数),那么a与b的最大公因数是( ),最小公倍数是( ) 。
15
1
b
42
a
45
(2)75是15和25的( )。
A.倍数 B.公因数 C.最小公倍数
(1)两个数的( )是有限的。
A.公因数 B.公倍数 C.倍数
3. 选一选。
(3)甲数和乙数的差是1(甲、乙为非0自然数),它们的最小公倍数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
C
D
4.公交车枢纽站3路车每3分钟发一次车,25路车每5分钟发一辆。这两路汽车同时发车后,至少再经过多少分钟又同时发车?
就是求3和5的最小公倍数是多少?
答:至少再经过15分钟又同时发车。
3的倍数有:3、6、9、12、15、18、21、24、27、30
…
5的倍数有:5、10、15、20、25、30
…
3和5的公倍数有15、30
…
5. 甲、乙、丙为三个相咬合的齿轮,使甲轮转6圈时,乙轮转7圈,丙轮转2圈。这三个齿轮的齿数最少应分别是多少齿?
三个齿轮转过的总齿数是6、7、2的公倍数。
三个齿轮转过的总齿数也应最少。
6、7和2的最小公倍数是42。
6、7和2的公倍数有:7, 14, 21, 28, 35, 42, 49, …
甲轮齿数:42÷6=7(齿)
乙轮齿数:42÷7=6(齿)
丙轮齿数:42÷2=21(齿)
答:甲、乙、丙三个齿轮最少分别是7齿、6齿和21齿。
*6.一种长方体香水盒长6cm,宽5cm,高10cm,如果在一个正方体箱子里刚好装满了一些这种香水盒,并且没有空隙,那么箱子的棱长至少是多少厘米?
6=2×3
答:箱子的棱长至少是30厘米。
6、5、10的最小公倍数是:2×3×5=30
5=1×5
10=2×5
*7.小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5圈,爸爸跑了10圈,妈妈跑了8圈。
同学们,这节课你有哪些收获?
公倍数和最小公倍数的应用
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一时间到达问题等等。
小学数学·五年级(下)·RJ
第11课时 最小公倍数的
应用
能够将生活中的实际问题转化为数学问题,提高解决问题的能力。
通过实际运用,进一步理解公倍数的意义,并能运用公倍数解决简单问题。
在参与中,体验学习和探索的乐趣,增强对数学学习的兴趣,获得成功体验。
能熟练地将生活中实际问题转化为求公倍数的问题。
知道问题中出现“最小”、“至少”等类似字眼时,运用“最小公倍数”来解决问题。
通过对信息和问题的分析,培养学生发现问题和解决问题的意识,培养推理能力。
在生活中,你见过贴瓷砖现象吗?
想一想:施工师傅在贴瓷砖之前需要进行哪些计算?
6的倍数有( )。
9的倍数有( )。
6和9的公倍数有( )。
6,12,18,24,30,36,···
9,18,27,36,45,54,···
18,36,···
求6和9的公倍数有哪些?
阅读习题,理解题意。
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
阅读习题你知道了哪些信息?
要求的问题是什么?
有哪些特殊要求?
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
1.长方形小瓷砖的规格:
知道了:
2dm
3dm
铺一个大的正方形
3.使用地砖须是:整数块
2.要铺地的形状是:
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
要解决的问题:
dm
用整块数长方形地砖铺成一个大正方形
2dm
3dm
正方形地面的边长可以是多少分米?
正方形地面的边长最小是多少分米?
运用公倍数的知识解决问题
要用整块的这种长方形墙砖铺出一个大的正方形。
可以先画一画,拼一拼尝试一下。
3dm
2dm
?dm
?dm
拼成的大正方形的边长可以是多少呢?
一种长方形地砖长3dm,宽2dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
自主探究
1. 用长3cm,宽2cm的卡片代替墙砖拼一拼。
2. 在格子图上画一画。
3. 边操作边思考:正方形的边长可以是多少分米 最小是多少分米
4. 同桌交流,说说你摆出的正方形边长是多少。
3dm
2dm
6dm
6dm
方法一:
方法二:
12dm
12dm
方法三:
边长: ?dm
拼成的大正方形的边长有什么共同点?
拼一拼,试一试:
我发现:正方形边长必须既是3的倍数,又是2的倍数。
3dm
2dm
?dm
?dm
那就是找2和3的公倍数来作为正方形地面的边长。
3的公倍数:3,6,9,12,15,18,···
2和
所以,可以铺出边长是 6dm、12dm、18dm、··· 的正方形,正方形边长最小是 6 dm。
答:正方形的边长可以是6分米、12分米、18分米、…最小是6分米。
在边长是6dm的正方形上画一画,看找得对不对。
解决这个问题的关键是把铺砖的问题转化成求公倍数的问题。
回顾与反思
达标练习,巩固成果
1.参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
40以内6和9的公倍数有18,36
答:可能是18人或36人。
(2)两个连续自然数的和是13,这两个数的最大公因数是( ),最小公倍数是( )。
(1)15和45的最大公因数是( ),最小公倍数是( )。
2. 填一填。
(3)如果a÷b=4(a、b为非0自然数),那么a与b的最大公因数是( ),最小公倍数是( ) 。
15
1
b
42
a
45
(2)75是15和25的( )。
A.倍数 B.公因数 C.最小公倍数
(1)两个数的( )是有限的。
A.公因数 B.公倍数 C.倍数
3. 选一选。
(3)甲数和乙数的差是1(甲、乙为非0自然数),它们的最小公倍数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
C
D
4.公交车枢纽站3路车每3分钟发一次车,25路车每5分钟发一辆。这两路汽车同时发车后,至少再经过多少分钟又同时发车?
就是求3和5的最小公倍数是多少?
答:至少再经过15分钟又同时发车。
3的倍数有:3、6、9、12、15、18、21、24、27、30
…
5的倍数有:5、10、15、20、25、30
…
3和5的公倍数有15、30
…
5. 甲、乙、丙为三个相咬合的齿轮,使甲轮转6圈时,乙轮转7圈,丙轮转2圈。这三个齿轮的齿数最少应分别是多少齿?
三个齿轮转过的总齿数是6、7、2的公倍数。
三个齿轮转过的总齿数也应最少。
6、7和2的最小公倍数是42。
6、7和2的公倍数有:7, 14, 21, 28, 35, 42, 49, …
甲轮齿数:42÷6=7(齿)
乙轮齿数:42÷7=6(齿)
丙轮齿数:42÷2=21(齿)
答:甲、乙、丙三个齿轮最少分别是7齿、6齿和21齿。
*6.一种长方体香水盒长6cm,宽5cm,高10cm,如果在一个正方体箱子里刚好装满了一些这种香水盒,并且没有空隙,那么箱子的棱长至少是多少厘米?
6=2×3
答:箱子的棱长至少是30厘米。
6、5、10的最小公倍数是:2×3×5=30
5=1×5
10=2×5
*7.小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5圈,爸爸跑了10圈,妈妈跑了8圈。
同学们,这节课你有哪些收获?
公倍数和最小公倍数的应用
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一时间到达问题等等。
