第12章因式分解复习课

课件18张PPT。《因式分解》—复习课复习目标：
1、进一步巩固因式分解的概念;
2、巩固因式分解常用的三种方法
3、选择恰当的方法进行因式分解
4、应用因式分解来解决一些实际问题
5、体验应用知识解决问题的乐趣一、知识要点（一）、因式分解的定义
（二）、因式分解的方法
（三）、因式分解的一般步骤自学指导
看本单元课本，完成以下要求
1、因式分解定义；
2、规律总结， 分解因式与整式乘法是互逆过程.
分解因式要注意的几点。
3、因式分解的方法
7分钟后，比一比，谁能快速而能准确解答相关问题（一）因式分解的定义： 把一个多项式化成几个整式的积的形式，叫做多项式的因式分解。
练习题：
一个多项式分解因式的结果为（x+3)(x+4),则这个多项式为（ ）
x2 ＋7 x ＋12即：一个多项式 →几个整式的积（二）因式分解的方法：（1）、提取公因式法
（2）、运用公式法
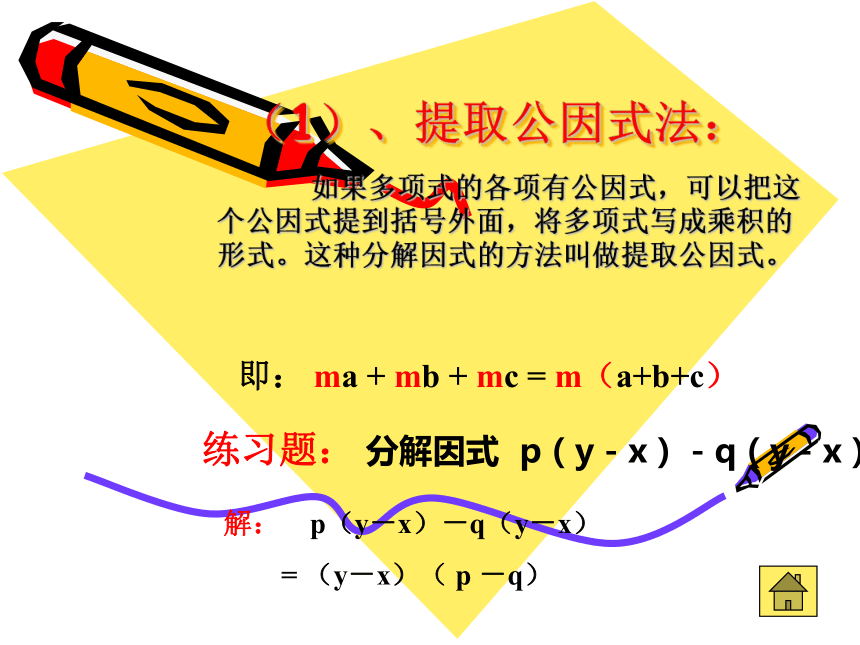
如果多项式的各项有公因式，可以把这个公因式提到括号外面，将多项式写成乘积的形式。这种分解因式的方法叫做提取公因式。
练习题： 分解因式 p（y－x）－q（y－x）（1）、提取公因式法：解： p（y－x）－q（y－x）
= （y－x）（ p －q）即： ma + mb + mc = m（a+b+c）（2）运用公式法： 如果把乘法公式反过来应用，就可以把多项式写成积的形式，达到分解因式目的。这种方法叫做公式法。
① a2－b2＝（a＋b）（a－b） [ 平方差公式 ] 练习 ② a2 ＋2ab＋ b2 ＝（a＋b）2 [ 完全平方和公式 ] 练习
a2 －2ab－ b2 ＝（a－b）2 [ 完全平方差公式 ]
公式法中主要使用的公式有如下几个：（三）因式分解的一般步骤：① 对任意多项式分解因式，都必须首先考虑提取公因式。 练习题 ② 考虑应用平方差公式或完全平方公式分解。
练习题：把下列各式分解因式：
（ x －y）3 － （ x －y）
a2 － x2y2

解： （ x －y）3 － （ x －y）
= （ x －y） （ x －y ＋ 1） （ x －y － 1） a2 － x2y2
=（a ＋xy）（ a － xy ）
练习题： 分解因式 x2－（2y）2
a2－b2＝（a＋b）（a－b） [ 平方差公式 ] 解： x2－（2y）2
=（x＋2y）（x－2y） 练习题：
下列各式能用完全平方公式分解因式的是（ ）
A、x2＋x＋2y2 B、 x2 ＋4x－4
C、x2＋4xy＋y2 D、 y2 －4xy＋4 x2
② a2 ＋2ab＋ b2 ＝（a＋b）2 a2 －2ab－ b2 ＝（a－b）2 D三、小结1、因式分解的定义： 把一个多项式化成几个整式的积的形式，叫做多项式的因式分解。
2、因式分解的方法：
（1）、提取公因式法（2）、运用公式法
因
式
分
解概念方法与整式乘法的关系：
相反变形提取公因式法公
式
法平方差公式 完全平方公式 四、作业1、把下列各式分解因式：
① 、1 －2ab － a2－ b2
②、2（x ＋ y）2 ＋ 5（x ＋ y）＋ 2
2、若5 x2 －4 xy ＋y2 － 2x ＋1=0，求x、y的值。3、把下列各式分解因式 （1） - 2xy - y2 - x2 （2） -1 + p4 （3）x2 - 2xy + y2 + 2x - 2y + 1 （4）( a - b)2n - (b - a)2n+1 4, 把 a2 - 4ab +3 b2 + 2bc - c2 因式分解。5, 已知：| x + y + 1| +| xy - 3 | = 0
求代数式xy3 + x3y 的值。6, 求证：913 - 324 能被8整除。 谢谢您的指导！ 再 见