二次函数复习2
图片预览




文档简介
课件19张PPT。驶向胜利的彼岸复习二次函数
复习目标1.理解二次函数概念4.会确定抛物线的顶点和对称轴,会对二次函数的图象
进行平移
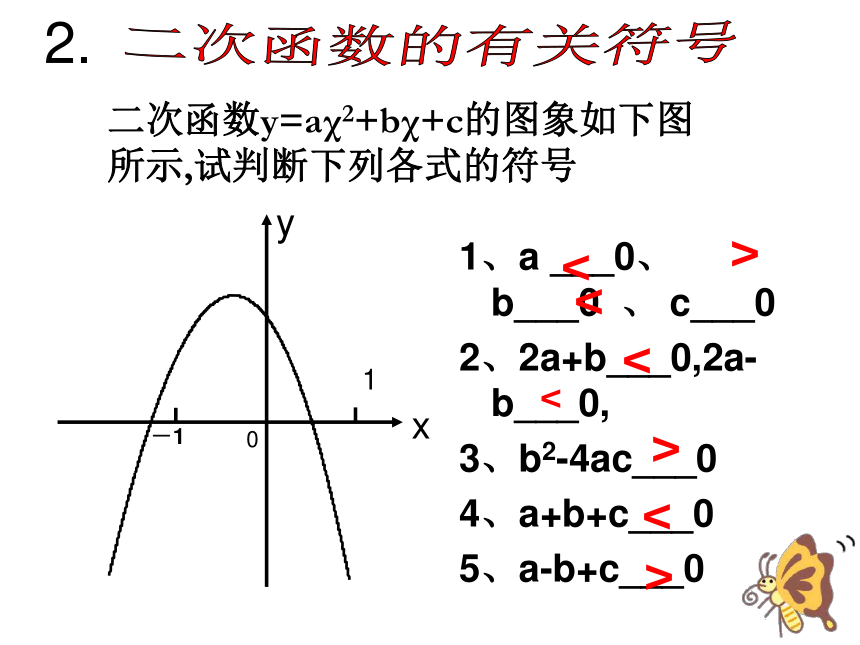
3.理解二次函数的符号特征2.掌握二次函数的图象和性质一.定义:一般地,形如y=ax2+bx+c(a,b,c是常数, a≠0)的函数叫做x的二次函数. 练习:当m=____时,函数y=(m+1)χ - 2χ+1 是二次函数?1m2+1二次函数有关知识点1、a ___0、 b___0 、 c___0
2、2a+b___0,2a-b___0,
3、b2-4ac___0
4、a+b+c___0
5、a-b+c___0
1二次函数y=aχ2+bχ+c的图象如下图所示,试判断下列各式的符号χ二次函数的有关符号2.>
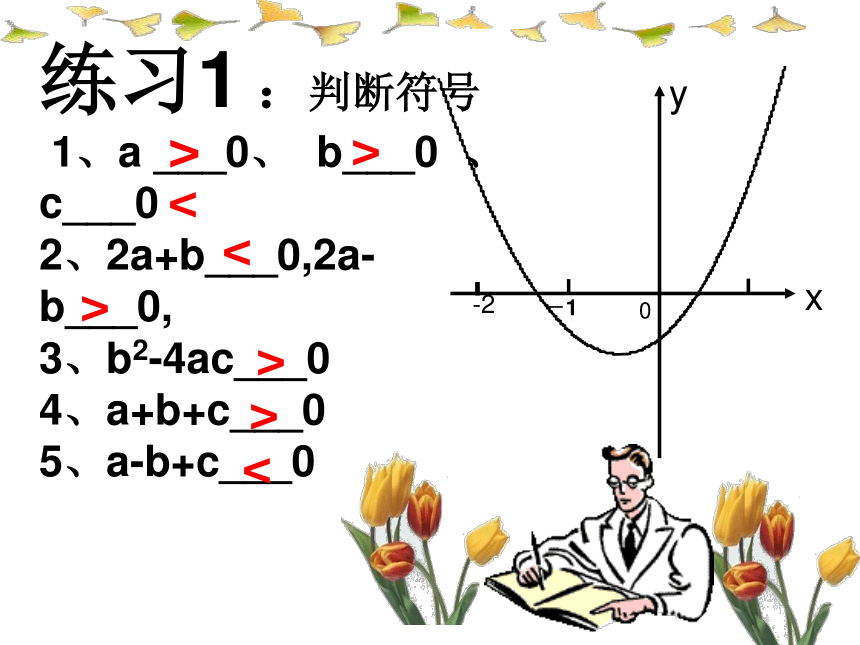
<<<<<<<练习1 :判断符号 1、a ___0、 b___0 、 c___0 2、2a+b___0,2a-b___0, 3、b2-4ac___0 4、a+b+c___0 5、a-b+c___0 -2><>>>><<练习2、如图为二次函数y =ax2+bx+c 的图象,给出下列说法.
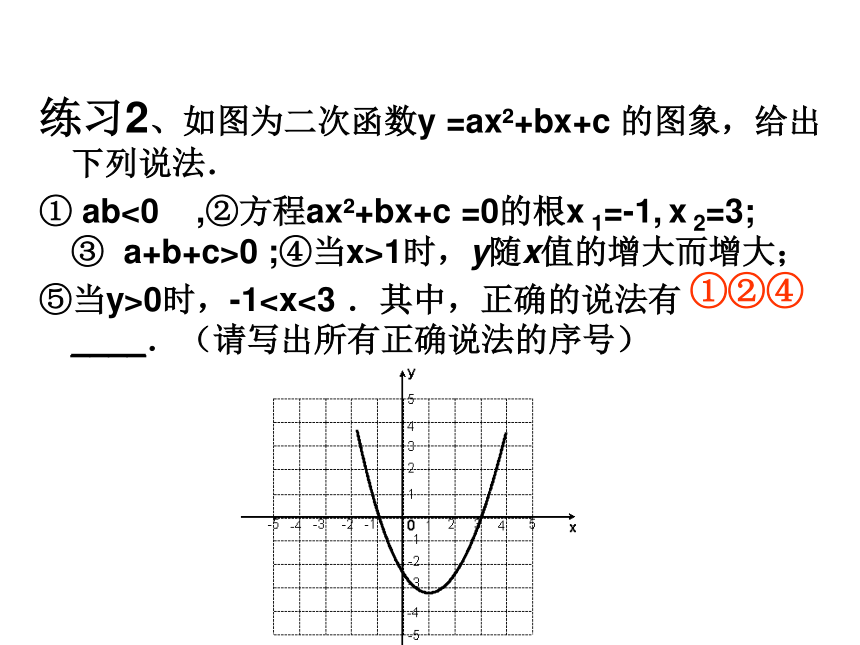
① ab<0 ,②方程ax2+bx+c =0的根x 1=-1, x 2=3; ③ a+b+c>0 ;④当x>1时,y随x值的增大而增大;
⑤当y>0时,-10 向下ao 负半轴c<0- 与1比较- 与-1比较与x轴交点个数令x=1,看纵坐标令x=-1,看纵坐标令x=2,看纵坐标令x=-2,看纵坐标小结二次函数 的图像的一部分如图所示,图像过点A(3,0),对称轴为 ,下列结论正确的个数为( ) 0 1 3 xy①b2 -4ac﹥0
②bc﹤0
③2a+b=0
④a+b+c=0
⑤方程 有两个大于1的实数根
⑥当x﹥1时,y随x的增大而增大A.1 B.2 C.3 D.4B 三.二次函数y=ax2+bx+c的图象与x轴公共点的个数及一元二次方程ax2+bx+c=0根的关系有两个交点有两个不相等的实数根b2-4ac > 0有一个公共点有两个相等的实数根b2-4ac = 0没有公共点没有实数根b2-4ac < 0 关系:二次函数y=ax2+bx+c的图象与x轴交点的横坐标是一元二次方程ax2+bx+c=0的根1、抛物线y=ax 2+bx+c 与x 轴有两个交点,则b 2-4ac _____0 ( )
A · ﹥ B · ﹤ C · = D ·不确定
2、已知 b 2-4ac ﹤0,那么抛物线
y=ax 2+bx+c与x 轴有________个公共点。
A0 3、抛物线y=ax 2+bx+c 与x 轴的只有一个公共点的坐标为(1,0),那么一元二次方程ax2+bx+c=0的根为____________.能力提升 已知二次函数的 图象,利用图象回答问题:
(1)方程 的根是什么?(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?(4)由图像你还能获得那些信息?①开口方向确定a
②对称轴确定a,b
③与y轴交点坐标,确定c
④ x取何值时y﹥0,y=0,y ﹤0 ⑤顶点坐标
⑥最值
⑦增减性
⑧特殊的值所得到的特殊的式子。(如x=1或x=-1)
⑨与x轴公共点个数
⑩ b 2 -4ac x 1=2, x 2=4(2)x<2或x>4
(3)2四.二次函数的表示形式直线x= 顶点坐标: 对称轴: 2.顶点式:y=a(x-h) +k(a≠0)顶点坐标: 对称轴:(h,k)X=h思考二次函数y=-3(x+2) 2 +4 图象是______,开口_____,对称轴是________,顶点坐标 是_________,当x_____时,函数y有最_____值,是_____,当 x _____时, y随x 的增大而减小,当 x________时, y随x 的增大而增大。抛物线向下=-2(-2,4)直线x=-2大4>-2<-2 ?(2013,山东枣庄)将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3 C.y=3(x+2)2-3 D.y=3(x-2)2-3 感知中考A五. 平移1.已知抛物线 ,配方后求:
(1)抛物线的开口方向,顶点A的坐标,对称轴,函数的最值,当x为何值时,y随的增大而减小?
(2)抛物线与x轴的交点B、C坐标,与y轴的交点D坐标。
(3)x为何值时,y<0?x为何值时,y>0 ?综合练习y=x2+2x-82、已知抛物线y=x2-kx+k+1,根据下列条件,求k的值
(1)顶点在Y轴上,k=_____。
(2)抛物线过点(-1,-2),k=____。
(3)抛物线的最小值
为-1 , k=_____。
0-2我知道了……
我学会了……
我能解决……
我在解决有关二次函数的
问题时应注意什么 …… 自学并完成学习报
第134页和第136—137页第1—13小题。不经历风雨,怎么见彩虹没有人能随随便便成功!再见基础 + 方法 = 能力!
复习目标1.理解二次函数概念4.会确定抛物线的顶点和对称轴,会对二次函数的图象
进行平移
3.理解二次函数的符号特征2.掌握二次函数的图象和性质一.定义:一般地,形如y=ax2+bx+c(a,b,c是常数, a≠0)的函数叫做x的二次函数. 练习:当m=____时,函数y=(m+1)χ - 2χ+1 是二次函数?1m2+1二次函数有关知识点1、a ___0、 b___0 、 c___0
2、2a+b___0,2a-b___0,
3、b2-4ac___0
4、a+b+c___0
5、a-b+c___0
1二次函数y=aχ2+bχ+c的图象如下图所示,试判断下列各式的符号χ二次函数的有关符号2.>
<<<<<<<练习1 :判断符号 1、a ___0、 b___0 、 c___0 2、2a+b___0,2a-b___0, 3、b2-4ac___0 4、a+b+c___0 5、a-b+c___0 -2><>>>><<练习2、如图为二次函数y =ax2+bx+c 的图象,给出下列说法.
① ab<0 ,②方程ax2+bx+c =0的根x 1=-1, x 2=3; ③ a+b+c>0 ;④当x>1时,y随x值的增大而增大;
⑤当y>0时,-1
②bc﹤0
③2a+b=0
④a+b+c=0
⑤方程 有两个大于1的实数根
⑥当x﹥1时,y随x的增大而增大A.1 B.2 C.3 D.4B 三.二次函数y=ax2+bx+c的图象与x轴公共点的个数及一元二次方程ax2+bx+c=0根的关系有两个交点有两个不相等的实数根b2-4ac > 0有一个公共点有两个相等的实数根b2-4ac = 0没有公共点没有实数根b2-4ac < 0 关系:二次函数y=ax2+bx+c的图象与x轴交点的横坐标是一元二次方程ax2+bx+c=0的根1、抛物线y=ax 2+bx+c 与x 轴有两个交点,则b 2-4ac _____0 ( )
A · ﹥ B · ﹤ C · = D ·不确定
2、已知 b 2-4ac ﹤0,那么抛物线
y=ax 2+bx+c与x 轴有________个公共点。
A0 3、抛物线y=ax 2+bx+c 与x 轴的只有一个公共点的坐标为(1,0),那么一元二次方程ax2+bx+c=0的根为____________.能力提升 已知二次函数的 图象,利用图象回答问题:
(1)方程 的根是什么?(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?(4)由图像你还能获得那些信息?①开口方向确定a
②对称轴确定a,b
③与y轴交点坐标,确定c
④ x取何值时y﹥0,y=0,y ﹤0 ⑤顶点坐标
⑥最值
⑦增减性
⑧特殊的值所得到的特殊的式子。(如x=1或x=-1)
⑨与x轴公共点个数
⑩ b 2 -4ac x 1=2, x 2=4(2)x<2或x>4
(3)2
A.y=3(x+2)2+3 B.y=3(x-2)2+3 C.y=3(x+2)2-3 D.y=3(x-2)2-3 感知中考A五. 平移1.已知抛物线 ,配方后求:
(1)抛物线的开口方向,顶点A的坐标,对称轴,函数的最值,当x为何值时,y随的增大而减小?
(2)抛物线与x轴的交点B、C坐标,与y轴的交点D坐标。
(3)x为何值时,y<0?x为何值时,y>0 ?综合练习y=x2+2x-82、已知抛物线y=x2-kx+k+1,根据下列条件,求k的值
(1)顶点在Y轴上,k=_____。
(2)抛物线过点(-1,-2),k=____。
(3)抛物线的最小值
为-1 , k=_____。
0-2我知道了……
我学会了……
我能解决……
我在解决有关二次函数的
问题时应注意什么 …… 自学并完成学习报
第134页和第136—137页第1—13小题。不经历风雨,怎么见彩虹没有人能随随便便成功!再见基础 + 方法 = 能力!
