2022-2023学年人教版八年级数学下册18.2特殊的平行四边形 基础训练 (无答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册18.2特殊的平行四边形 基础训练 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 21:19:58 | ||
图片预览

文档简介
18.2 特殊的平行四边形
一、单选题
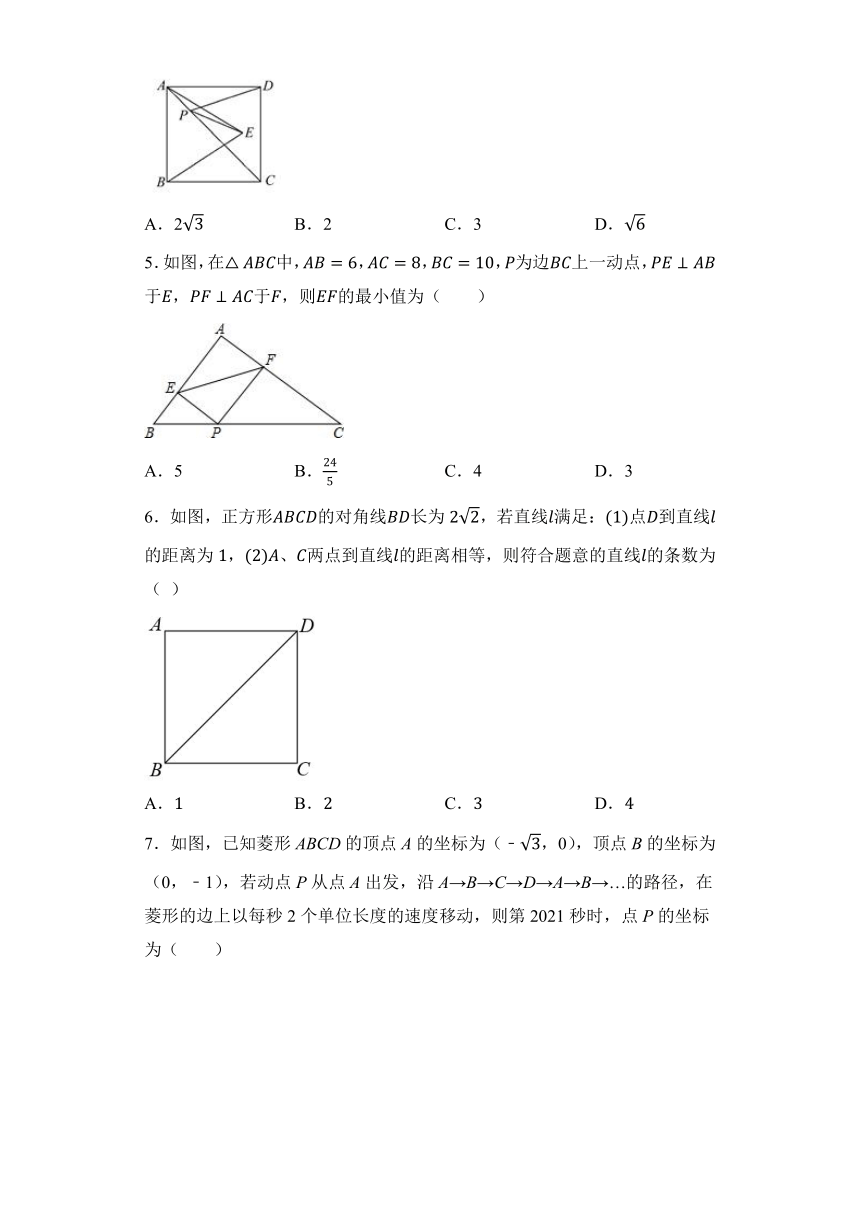
1.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28 B.24 C.14 D.18
2.如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
3.如图,正方形ABCD的对角线AC、BD交于点O,AO=3,则AB的长为( )
A.2 B.3 C. D.
4.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( )
A.2 B.2 C.3 D.
5.如图,在中,,,,为边上一动点,于,于,则的最小值为( )
A.5 B. C.4 D.3
6.如图,正方形的对角线长为,若直线满足:点到直线的距离为,、两点到直线的距离相等,则符合题意的直线的条数为( )
A. B. C. D.
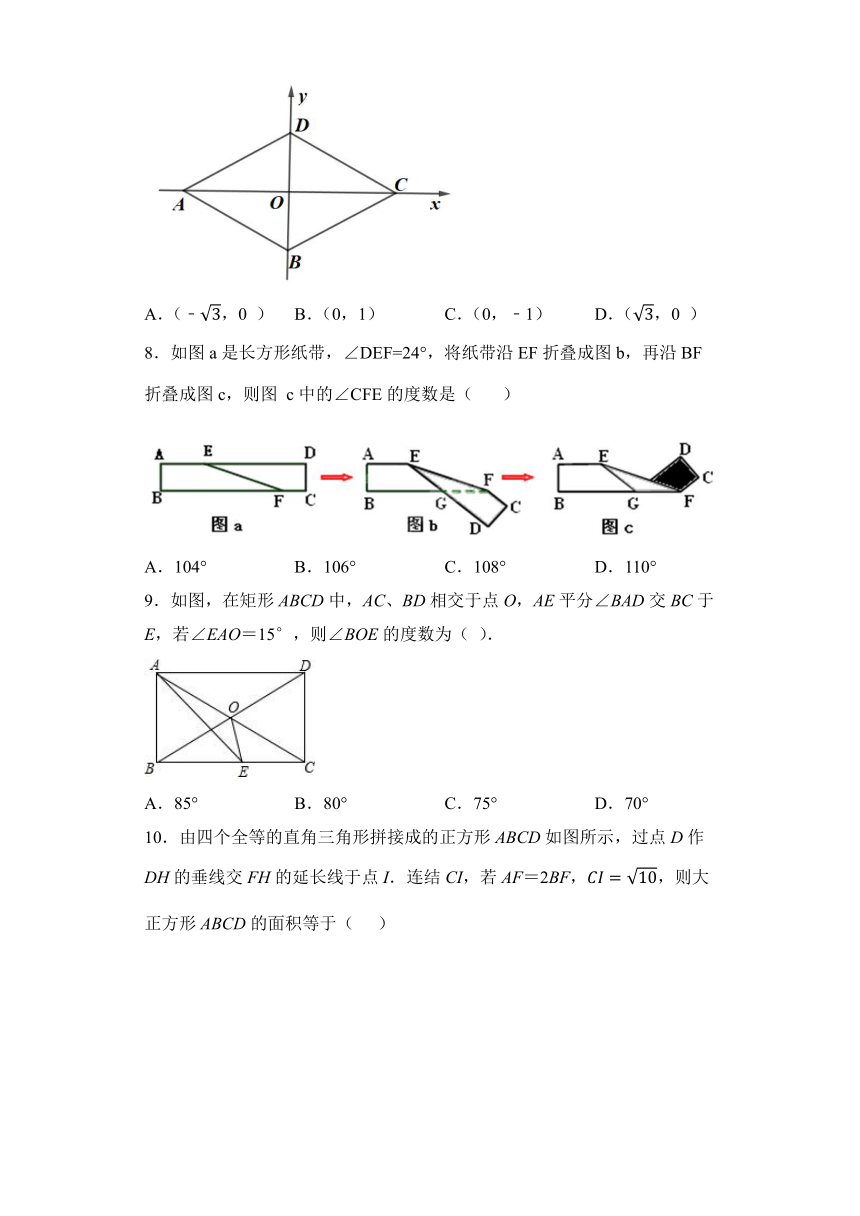
7.如图,已知菱形ABCD的顶点A的坐标为(﹣,0),顶点B的坐标为(0,﹣1),若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒2个单位长度的速度移动,则第2021秒时,点P的坐标为( )
A.(﹣,0 ) B.(0,1) C.(0,﹣1) D.(,0 )
8.如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图 c中的∠CFE的度数是( )
A.104° B.106° C.108° D.110°
9.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( ).
A.85° B.80° C.75° D.70°
10.由四个全等的直角三角形拼接成的正方形ABCD如图所示,过点D作DH的垂线交FH的延长线于点I.连结CI,若AF=2BF,,则大正方形ABCD的面积等于( )
A.4 B.5 C.8 D.10
二、填空题
11.矩形 ABCD 的一组邻边分别为 1 和 4,若点 E 为边 AD 上一点, 且 AE=,则EC=_______.
12.如图,在中,,,,点,分别在,上,将沿直线翻折,点的对应点恰好落在上,连接,若,则的长为_________.
13.如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且,则EG的长是________.
14.如图,正方形ABCD中,点E、F分别在边BC、CD上,连接AE、EF、AF,且∠EAF=45°,下列结论:
①△ABE≌△ADF;
②∠AEB=∠AEF;
③正方形ABCD的周长=2△CEF的周长;
④S△ABE+S△ADF=S△CEF,其中正确的是_____.(只填写序号)
15.如图1,分别沿长方形纸片和正方形纸片的对角线、剪开,拼成如图2所示的,若中间空白部分四边形恰好是正方形,且的面积为,则正方形的面积为________.
三、解答题
16.判定一个四边形是正方形,你有哪些方法?
17.已知:AC是菱形ABCD的对角线,延长CB至点E,使得BE=BC,连接AE.
(1)如图1,求证:AE⊥AC;
(2)如图2,过点D作DF⊥AB,垂足为点F,若AE=6,CE=10,求DF的长.
18.我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a,高为h的三角形的面积公式为.想法是:以为边作矩形,点A在边上,再过点A作的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A作的垂线交于点D.(只保留作图痕迹)
在和中,
∵,
∴.
∵,
∴______①____.
∵,
∴______②_____.
又∵____③______.
∴().
同理可得:_____④______.
.
19.如图,在中,,B、E分别是FC、AB的中点,过点A作交FE的延长线于点D.
(1)求证:.
(2)求证:四边形ABCD是菱形.
20.如图1,点Q是正方形ABCD边BC的中点,点P在BC延长线上,CR平分∠DCP,AQ⊥QR于Q.(本题不需要写理由)
(1)求证AQ=QR;
(2)如图2,若将条件中的点Q改为BC边上的任意一点,其余条件不变,AQ=QR是否依然成立?若成立,请证明你的结论;若不成立,请说明理由;
(3)若将第(2)小题中的正方形改为正n边型ABCD…(n为大于等于3的正整数),点Q为BC边上的任意一点,点P在BC延长线上,CR平分∠DCP,则当∠AQR= °时,AQ=QR.(用n表示,直接写出结果,无需证明)
21.如图,在正方形中,是上的一点,连接,过点作交外角平分线于.
(1)若,求的长;
(2)如图2,连接,交边于点F,连接.求证:平分.
一、单选题
1.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.若四边形CDEF的周长是10cm,AC的长为4cm,则△ABC的周长是( )
A.28 B.24 C.14 D.18
2.如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是( )
A.24 B.25 C.30 D.36
3.如图,正方形ABCD的对角线AC、BD交于点O,AO=3,则AB的长为( )
A.2 B.3 C. D.
4.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 ( )
A.2 B.2 C.3 D.
5.如图,在中,,,,为边上一动点,于,于,则的最小值为( )
A.5 B. C.4 D.3
6.如图,正方形的对角线长为,若直线满足:点到直线的距离为,、两点到直线的距离相等,则符合题意的直线的条数为( )
A. B. C. D.
7.如图,已知菱形ABCD的顶点A的坐标为(﹣,0),顶点B的坐标为(0,﹣1),若动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒2个单位长度的速度移动,则第2021秒时,点P的坐标为( )
A.(﹣,0 ) B.(0,1) C.(0,﹣1) D.(,0 )
8.如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图 c中的∠CFE的度数是( )
A.104° B.106° C.108° D.110°
9.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( ).
A.85° B.80° C.75° D.70°
10.由四个全等的直角三角形拼接成的正方形ABCD如图所示,过点D作DH的垂线交FH的延长线于点I.连结CI,若AF=2BF,,则大正方形ABCD的面积等于( )
A.4 B.5 C.8 D.10
二、填空题
11.矩形 ABCD 的一组邻边分别为 1 和 4,若点 E 为边 AD 上一点, 且 AE=,则EC=_______.
12.如图,在中,,,,点,分别在,上,将沿直线翻折,点的对应点恰好落在上,连接,若,则的长为_________.
13.如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且,则EG的长是________.
14.如图,正方形ABCD中,点E、F分别在边BC、CD上,连接AE、EF、AF,且∠EAF=45°,下列结论:
①△ABE≌△ADF;
②∠AEB=∠AEF;
③正方形ABCD的周长=2△CEF的周长;
④S△ABE+S△ADF=S△CEF,其中正确的是_____.(只填写序号)
15.如图1,分别沿长方形纸片和正方形纸片的对角线、剪开,拼成如图2所示的,若中间空白部分四边形恰好是正方形,且的面积为,则正方形的面积为________.
三、解答题
16.判定一个四边形是正方形,你有哪些方法?
17.已知:AC是菱形ABCD的对角线,延长CB至点E,使得BE=BC,连接AE.
(1)如图1,求证:AE⊥AC;
(2)如图2,过点D作DF⊥AB,垂足为点F,若AE=6,CE=10,求DF的长.
18.我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a,高为h的三角形的面积公式为.想法是:以为边作矩形,点A在边上,再过点A作的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:证明:用直尺和圆规过点A作的垂线交于点D.(只保留作图痕迹)
在和中,
∵,
∴.
∵,
∴______①____.
∵,
∴______②_____.
又∵____③______.
∴().
同理可得:_____④______.
.
19.如图,在中,,B、E分别是FC、AB的中点,过点A作交FE的延长线于点D.
(1)求证:.
(2)求证:四边形ABCD是菱形.
20.如图1,点Q是正方形ABCD边BC的中点,点P在BC延长线上,CR平分∠DCP,AQ⊥QR于Q.(本题不需要写理由)
(1)求证AQ=QR;
(2)如图2,若将条件中的点Q改为BC边上的任意一点,其余条件不变,AQ=QR是否依然成立?若成立,请证明你的结论;若不成立,请说明理由;
(3)若将第(2)小题中的正方形改为正n边型ABCD…(n为大于等于3的正整数),点Q为BC边上的任意一点,点P在BC延长线上,CR平分∠DCP,则当∠AQR= °时,AQ=QR.(用n表示,直接写出结果,无需证明)
21.如图,在正方形中,是上的一点,连接,过点作交外角平分线于.
(1)若,求的长;
(2)如图2,连接,交边于点F,连接.求证:平分.
