19.1.1变量与函数课件
图片预览








文档简介
课件22张PPT。万物皆变 第19章 一次函数第十九章 一次函数 阅读章引言问题探究:问题1:在事物的运动变化中,一个量随另一个量变化而变化的现象大量存在,请你再举出一个具有这种特征的相关例子加以说明.问题2:为了刻画变量之间相互依存和变化的关系,我们形成了什么概念?为了更深入地认识现实世界中运动变化的规律,我们需要研究什么内容?问题3:本章我们将主要学习哪些内容?将从哪些方面来展开研究?19.1.1 变量与函数 第1课时【学习目标】
1 认识变量、常量;
2学会用含一个变量的代数式表示另一个变量.
【学习重点】
认识变量、常量;用式子表示变量间关系. 【学习难点】
用含有一个变量的式子表示另一个变量. 学生问教材(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.①请根据题意填写下表:
②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含t的式子表示s: (2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含x的式子表示y:
④y的值随x的值的变化而变化吗?(3)圆形水波慢慢地扩大,在这一过程中,当圆的
半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别
为多少?①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
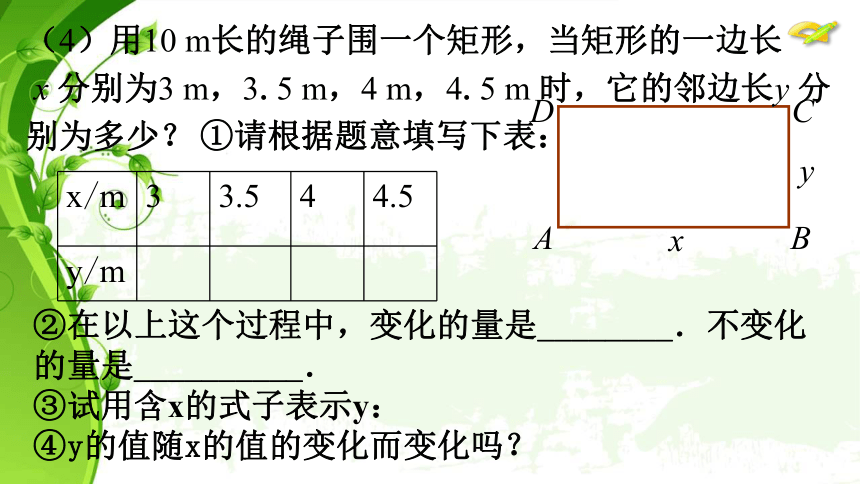
③试用含r的式子表示S: (4)用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含x的式子表示y:
④y的值随x的值的变化而变化吗?
说一说数值不断
变化的量变量数值固定
不变的量常量 上述运动变化过程中出现的数量,你认为可以怎样
分类?在一个变化过程中,我们称数值发生了变化的量为变量,数值始终不变的量为常量. 在同一个变化过程中,理解变量与常量的关键词分别是:发生了变化和始终不变.形成概念
1.指出下列变化过程中的变量和常量:
①某市的自来水价为4元/t,现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费为y元.
②某地手机通话费为0.2元/min.李明在手机话费卡中存入30元,记此后他的手机通话时间为t min,话费卡中的余额为元.
学生问学生③水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率为.
④把10本书随意放入两个抽屉,第一个抽屉放入x本,第二个抽屉放入y本.2、写出下列各问题中所满足的关系式,并指出各个关系式中,哪些量是变量,哪些量是常量?
①用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与一边长x(m)之间的关系式;
②购买单价是0.4元的铅笔,总金额y(元)与 购买的铅笔的数量n(支)的关系;
③运动员在4000m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步的速度v(m/s)的关系;
④某种活期储蓄的月利率为0.16%,存10000元本金,按国家规定,取款时,应缴纳利息部分的20%的利息税,求这种活期储蓄扣除利息税后实得的本息和y(元)与所存月数x之间的关系式.
⑤瓶子或罐头盒等物体常如下图那样堆放.试确定瓶子总数y与层数x之间的关系式.
本节课的收获是什么?课堂小结老师问学生1、某种报纸的价格是每份0.4元,买x份报纸的总价为y元,先填写下表,再用含x的式子表示y.
x与y之间的关系是_________________.
2、长方形相邻两边长分别为x、y,面积为30,则用含x的式子表示y为______ ______,这个问题中,____________常量;__________是变量.3、写出下列问题中的关系式,并指出其中的变量和常量.(1)直角三角形中一个锐角α与另一个锐角β之间的关系.
(2)多边形的内角和W与边数n的关系.(3)一盛满30吨水的水箱,每小时流出0.5 吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
(4)甲、乙两地相距y千米,一自行车以每小时10千米的速度从甲地驶向乙地,试用行驶时间t(小时)表示自行车离乙地的距离S(千米).
1 认识变量、常量;
2学会用含一个变量的代数式表示另一个变量.
【学习重点】
认识变量、常量;用式子表示变量间关系. 【学习难点】
用含有一个变量的式子表示另一个变量. 学生问教材(1)汽车以60 km/h 的速度匀速行驶,行驶时间为 t h,行驶路程为 s km.①请根据题意填写下表:
②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含t的式子表示s: (2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含x的式子表示y:
④y的值随x的值的变化而变化吗?(3)圆形水波慢慢地扩大,在这一过程中,当圆的
半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别
为多少?①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含r的式子表示S: (4)用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?①请根据题意填写下表:②在以上这个过程中,变化的量是________.不变化的量是__________.
③试用含x的式子表示y:
④y的值随x的值的变化而变化吗?
说一说数值不断
变化的量变量数值固定
不变的量常量 上述运动变化过程中出现的数量,你认为可以怎样
分类?在一个变化过程中,我们称数值发生了变化的量为变量,数值始终不变的量为常量. 在同一个变化过程中,理解变量与常量的关键词分别是:发生了变化和始终不变.形成概念
1.指出下列变化过程中的变量和常量:
①某市的自来水价为4元/t,现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费为y元.
②某地手机通话费为0.2元/min.李明在手机话费卡中存入30元,记此后他的手机通话时间为t min,话费卡中的余额为元.
学生问学生③水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率为.
④把10本书随意放入两个抽屉,第一个抽屉放入x本,第二个抽屉放入y本.2、写出下列各问题中所满足的关系式,并指出各个关系式中,哪些量是变量,哪些量是常量?
①用总长为60m的篱笆围成矩形场地,求矩形的面积S(m2)与一边长x(m)之间的关系式;
②购买单价是0.4元的铅笔,总金额y(元)与 购买的铅笔的数量n(支)的关系;
③运动员在4000m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步的速度v(m/s)的关系;
④某种活期储蓄的月利率为0.16%,存10000元本金,按国家规定,取款时,应缴纳利息部分的20%的利息税,求这种活期储蓄扣除利息税后实得的本息和y(元)与所存月数x之间的关系式.
⑤瓶子或罐头盒等物体常如下图那样堆放.试确定瓶子总数y与层数x之间的关系式.
本节课的收获是什么?课堂小结老师问学生1、某种报纸的价格是每份0.4元,买x份报纸的总价为y元,先填写下表,再用含x的式子表示y.
x与y之间的关系是_________________.
2、长方形相邻两边长分别为x、y,面积为30,则用含x的式子表示y为______ ______,这个问题中,____________常量;__________是变量.3、写出下列问题中的关系式,并指出其中的变量和常量.(1)直角三角形中一个锐角α与另一个锐角β之间的关系.
(2)多边形的内角和W与边数n的关系.(3)一盛满30吨水的水箱,每小时流出0.5 吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
(4)甲、乙两地相距y千米,一自行车以每小时10千米的速度从甲地驶向乙地,试用行驶时间t(小时)表示自行车离乙地的距离S(千米).
