2014年湖南省下东中学数学中考专题复习:解直角三角形
文档属性
| 名称 | 2014年湖南省下东中学数学中考专题复习:解直角三角形 | 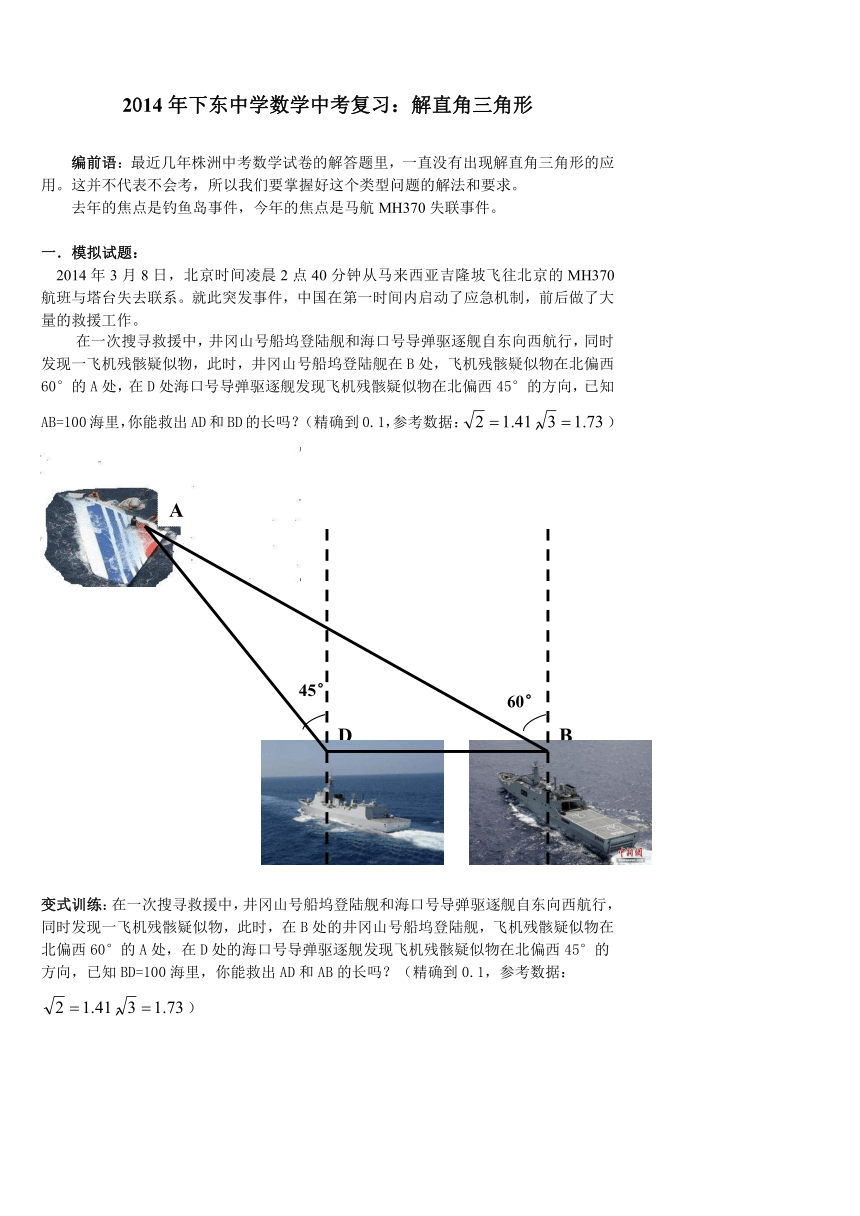 | |
| 格式 | zip | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-09 21:20:41 | ||
图片预览

文档简介
2014年下东中学数学中考复习:解直角三角形
编前语:最近几年株洲中考数学试卷的解答题里,一直没有出现解直角三角形的应用。这并不代表不会考,所以我们要掌握好这个类型问题的解法和要求。
去年的焦点是钓鱼岛事件,今年的焦点是马航MH370失联事件。
一.模拟试题:
2014年3月8日,北京时间凌晨2点40 ( http: / / www.21cnjy.com )分钟从马来西亚吉隆坡飞往北京的MH370航班与塔台失去联系。就此突发事件,中国在第一时间内启动了应急机制,前后做了大量的救援工作。
在一次搜寻救援中,井冈山号船坞登陆舰和海口号导弹驱逐舰自东向西航行,同时发现一飞机残骸疑似物,此时,井冈山号船坞登陆舰在B处,飞机残骸疑似物在北偏西60°的A处,在D处海口号导弹驱逐舰发现飞机残骸疑似物在北偏西45°的方向,已知AB=100海里,你能救出AD和BD的长吗?(精确到0.1,参考数据: HYPERLINK "http://www.21cnjy.com" )
变式训练:在一次搜寻救援中,井冈山号船坞登陆舰和海口号导弹驱逐舰自东向西航行,同时发现一飞机残骸疑似物,此时,在B处的井冈山号船坞登陆舰,飞机残骸疑似物在北偏西60°的A处,在D处的海口号导弹驱逐舰发现飞机残骸疑似物在北偏西45°的方向,已知BD=100海里,你能救出AD和AB的长吗?(精确到0.1,参考数据: HYPERLINK "http://www.21cnjy.com" )
二.模拟训练:
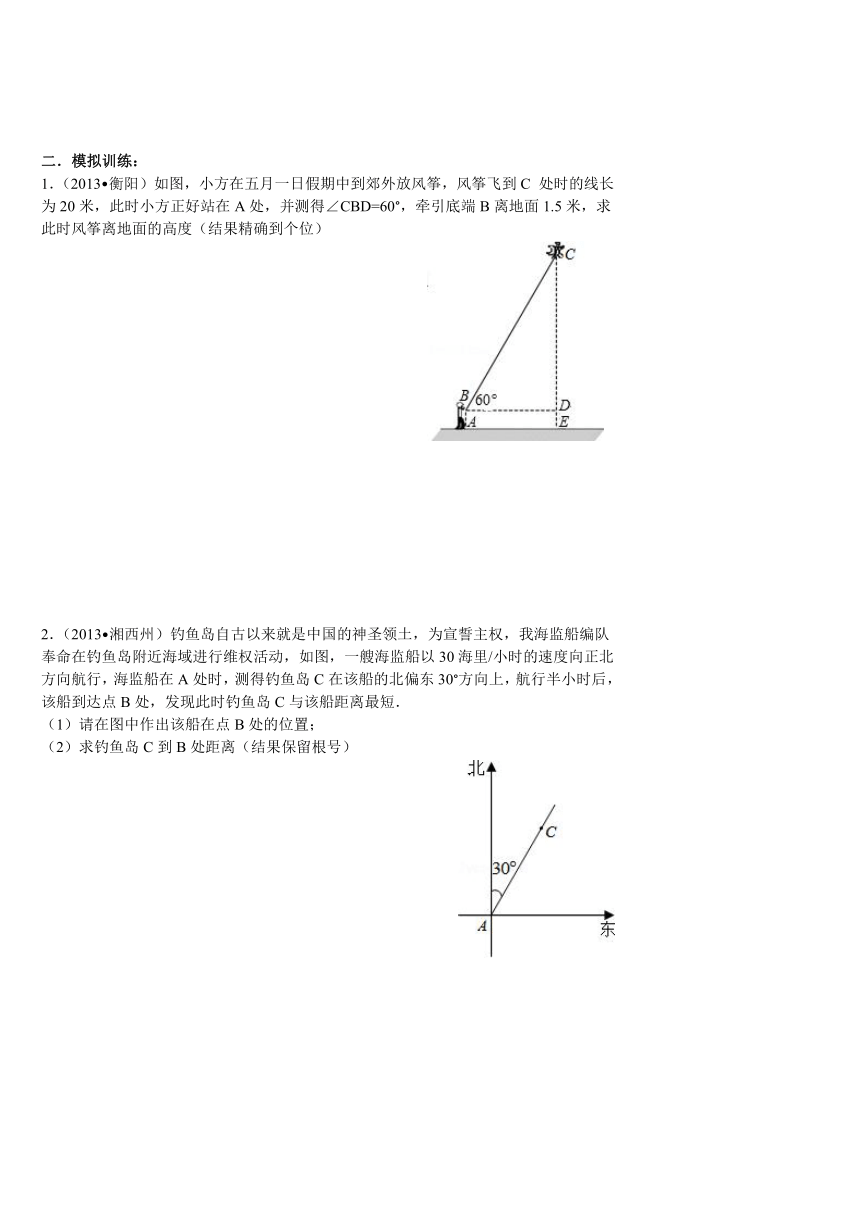
1.(2013 衡阳)如图,小方在五月一日 ( http: / / www.21cnjy.com )假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度(结果精确到个位)
( http: / / www.21cnjy.com )
2.(2013 湘西州)钓鱼岛自古以来就是 ( http: / / www.21cnjy.com )中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.
(1)请在图中作出该船在点B处的位置;
(2)求钓鱼岛C到B处距离(结果保留根号)
( http: / / www.21cnjy.com )
3.(2013 益阳)如图 ( http: / / www.21cnjy.com ),益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62 ( http: / / www.21cnjy.com ),cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
( http: / / www.21cnjy.com )
4.(2013湘潭)如图,C岛位于我南海A港口北偏东60°方向,距A港口 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 海里处.我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°的方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时
5.(2013 张家界)国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化
立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶
F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据
此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: ( http: / / www.21cnjy.com )=1.732, ( http: / / www.21cnjy.com )=1.414)
( http: / / www.21cnjy.com )
6.(2013岳阳)某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE
为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行
改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求(结果保留根号);
(2)在楼梯口B左侧正前方距离舞台底部C点3m处有一株大树,修新楼梯AD时底端D
是否会触到大树?并说明理由。
( http: / / www.21cnjy.com )
45°
60°
B
D
A
A
北
东
C
D
B
(第4题图)
60°
45°
编前语:最近几年株洲中考数学试卷的解答题里,一直没有出现解直角三角形的应用。这并不代表不会考,所以我们要掌握好这个类型问题的解法和要求。
去年的焦点是钓鱼岛事件,今年的焦点是马航MH370失联事件。
一.模拟试题:
2014年3月8日,北京时间凌晨2点40 ( http: / / www.21cnjy.com )分钟从马来西亚吉隆坡飞往北京的MH370航班与塔台失去联系。就此突发事件,中国在第一时间内启动了应急机制,前后做了大量的救援工作。
在一次搜寻救援中,井冈山号船坞登陆舰和海口号导弹驱逐舰自东向西航行,同时发现一飞机残骸疑似物,此时,井冈山号船坞登陆舰在B处,飞机残骸疑似物在北偏西60°的A处,在D处海口号导弹驱逐舰发现飞机残骸疑似物在北偏西45°的方向,已知AB=100海里,你能救出AD和BD的长吗?(精确到0.1,参考数据: HYPERLINK "http://www.21cnjy.com" )
变式训练:在一次搜寻救援中,井冈山号船坞登陆舰和海口号导弹驱逐舰自东向西航行,同时发现一飞机残骸疑似物,此时,在B处的井冈山号船坞登陆舰,飞机残骸疑似物在北偏西60°的A处,在D处的海口号导弹驱逐舰发现飞机残骸疑似物在北偏西45°的方向,已知BD=100海里,你能救出AD和AB的长吗?(精确到0.1,参考数据: HYPERLINK "http://www.21cnjy.com" )
二.模拟训练:
1.(2013 衡阳)如图,小方在五月一日 ( http: / / www.21cnjy.com )假期中到郊外放风筝,风筝飞到C 处时的线长为20米,此时小方正好站在A处,并测得∠CBD=60°,牵引底端B离地面1.5米,求此时风筝离地面的高度(结果精确到个位)
( http: / / www.21cnjy.com )
2.(2013 湘西州)钓鱼岛自古以来就是 ( http: / / www.21cnjy.com )中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.
(1)请在图中作出该船在点B处的位置;
(2)求钓鱼岛C到B处距离(结果保留根号)
( http: / / www.21cnjy.com )
3.(2013 益阳)如图 ( http: / / www.21cnjy.com ),益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62 ( http: / / www.21cnjy.com ),cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
( http: / / www.21cnjy.com )
4.(2013湘潭)如图,C岛位于我南海A港口北偏东60°方向,距A港口 HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 海里处.我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°的方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时
5.(2013 张家界)国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化
立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰顶
F点的俯角为30°,保持方向不变前进1200米到达B点后测得F点俯角为45°,如图2.请据
此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值: ( http: / / www.21cnjy.com )=1.732, ( http: / / www.21cnjy.com )=1.414)
( http: / / www.21cnjy.com )
6.(2013岳阳)某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE
为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行
改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求(结果保留根号);
(2)在楼梯口B左侧正前方距离舞台底部C点3m处有一株大树,修新楼梯AD时底端D
是否会触到大树?并说明理由。
( http: / / www.21cnjy.com )
45°
60°
B
D
A
A
北
东
C
D
B
(第4题图)
60°
45°
同课章节目录
