2014年湖南省下东中学数学中考专题复习:动点最值问题
文档属性
| 名称 | 2014年湖南省下东中学数学中考专题复习:动点最值问题 |  | |
| 格式 | zip | ||
| 文件大小 | 173.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-09 21:22:24 | ||
图片预览


文档简介
2014年下东中学数学中考复习:动点最值问题
一.株洲最近几年中考试题:
年 份 内 容 分值
2013年中考 相似三角形的判定与性质; 8分
2012年中考 相似三角形的判定与性质;二次函数的最值。 8分
2011年中考 △全等的判定;勾股定理。 8分
2010年中考 相似三角形的判定与性质;二次函数的最值。 8分
2009年中考 相似三角形的判定与性质;二次函数的最值。 10分
二.中考真题:
1.(2013 株洲)已知在△ABC中, ( http: / / www.21cnjy.com )∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
( http: / / www.21cnjy.com )
2.(2012 株洲)如图,在△ABC中, ( http: / / www.21cnjy.com )∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
( http: / / www.21cnjy.com )
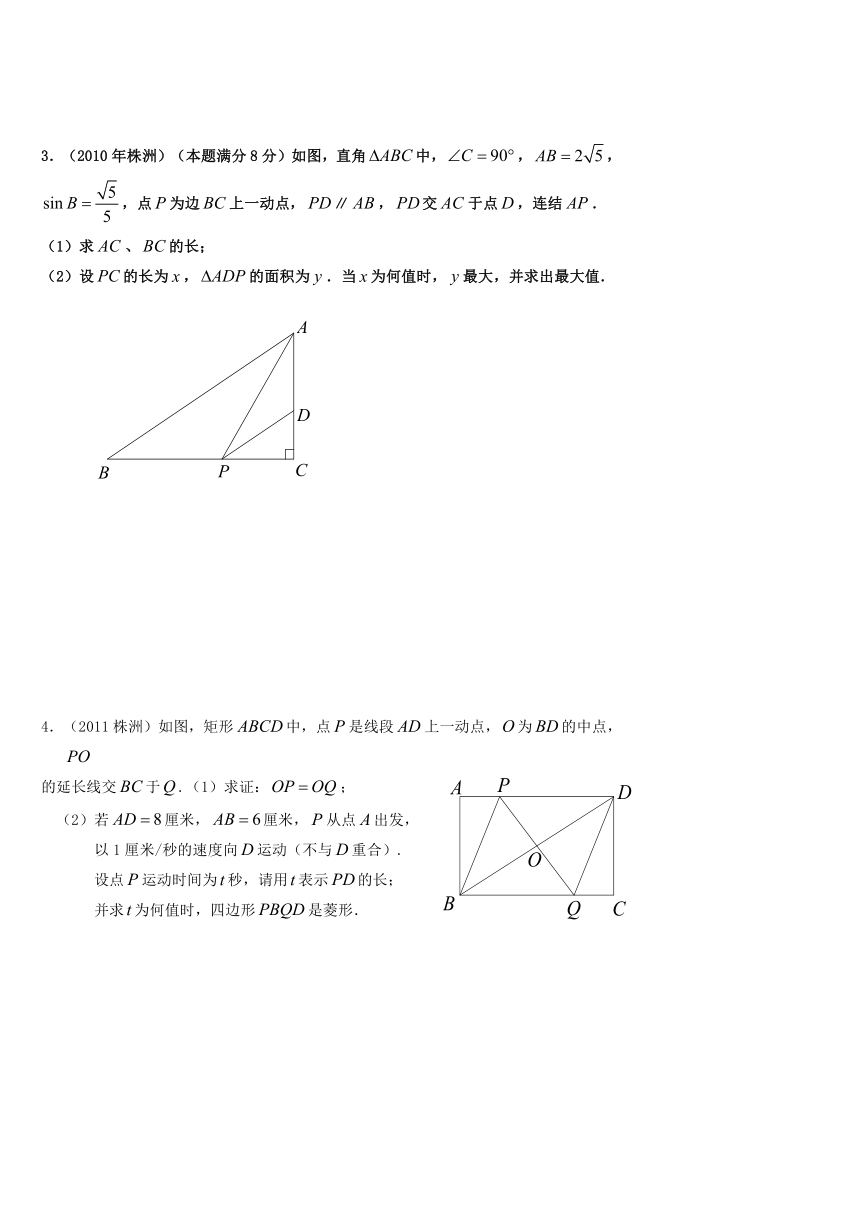
3.(2010年株洲)(本题满分8分)如图,直角 HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,点 HYPERLINK "http://www.21cnjy.com" 为边 HYPERLINK "http://www.21cnjy.com" 上一动点, HYPERLINK "http://www.21cnjy.com" ∥ HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" ,连结 HYPERLINK "http://www.21cnjy.com" .
(1)求 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 的长;
(2)设 HYPERLINK "http://www.21cnjy.com" 的长为 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的面积为 HYPERLINK "http://www.21cnjy.com" .当 HYPERLINK "http://www.21cnjy.com" 为何值时, HYPERLINK "http://www.21cnjy.com" 最大,并求出最大值.
4.(2011株洲)如图,矩形 HYPERLINK "http://www.21cnjy.com" 中,点 HYPERLINK "http://www.21cnjy.com" 是线段 HYPERLINK "http://www.21cnjy.com" 上一动点, HYPERLINK "http://www.21cnjy.com" 为 HYPERLINK "http://www.21cnjy.com" 的中点, HYPERLINK "http://www.21cnjy.com"
的延长线交 HYPERLINK "http://www.21cnjy.com" 于 HYPERLINK "http://www.21cnjy.com" .(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)若 HYPERLINK "http://www.21cnjy.com" 厘米, HYPERLINK "http://www.21cnjy.com" 厘米, HYPERLINK "http://www.21cnjy.com" 从点 HYPERLINK "http://www.21cnjy.com" 出发,
以1厘米/秒的速度向 HYPERLINK "http://www.21cnjy.com" 运动(不与 HYPERLINK "http://www.21cnjy.com" 重合).
设点 HYPERLINK "http://www.21cnjy.com" 运动时间为 HYPERLINK "http://www.21cnjy.com" 秒,请用 HYPERLINK "http://www.21cnjy.com" 表示 HYPERLINK "http://www.21cnjy.com" 的长;
并求 HYPERLINK "http://www.21cnjy.com" 为何值时,四边形 HYPERLINK "http://www.21cnjy.com" 是菱形.
5.(2009年株洲)(本题满分10分)如图1, HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,点 HYPERLINK "http://www.21cnjy.com"
在线段 HYPERLINK "http://www.21cnjy.com" 上运动,点 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别在线段 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上,且使得四边形 HYPERLINK "http://www.21cnjy.com" 是矩形.设
HYPERLINK "http://www.21cnjy.com" 的长为 HYPERLINK "http://www.21cnjy.com" ,矩形 HYPERLINK "http://www.21cnjy.com" 的面积为 HYPERLINK "http://www.21cnjy.com" ,已知 HYPERLINK "http://www.21cnjy.com" 是 HYPERLINK "http://www.21cnjy.com" 的函数,其图象是过点(12,36)的
抛物线的一部分(如图2所示). (1)求 HYPERLINK "http://www.21cnjy.com" 的长;
(2)当 HYPERLINK "http://www.21cnjy.com" 为何值时,矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大,并求出最大值.
为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:
张明:图2中的抛物线过点(12,36)在图1中表示什么呢?
李明:因为抛物线上的点是表示图1中的长与矩形面积的对应关系,
那么,(12,36)表示当时,的长与矩形面积的对应关系.
赵明:对,我知道纵坐标36是什么意思了!
孔明:哦,这样就可以算出,这个问题就可以解决了.
请根据上述对话,帮他们解答这个问题.
三.模拟训练:
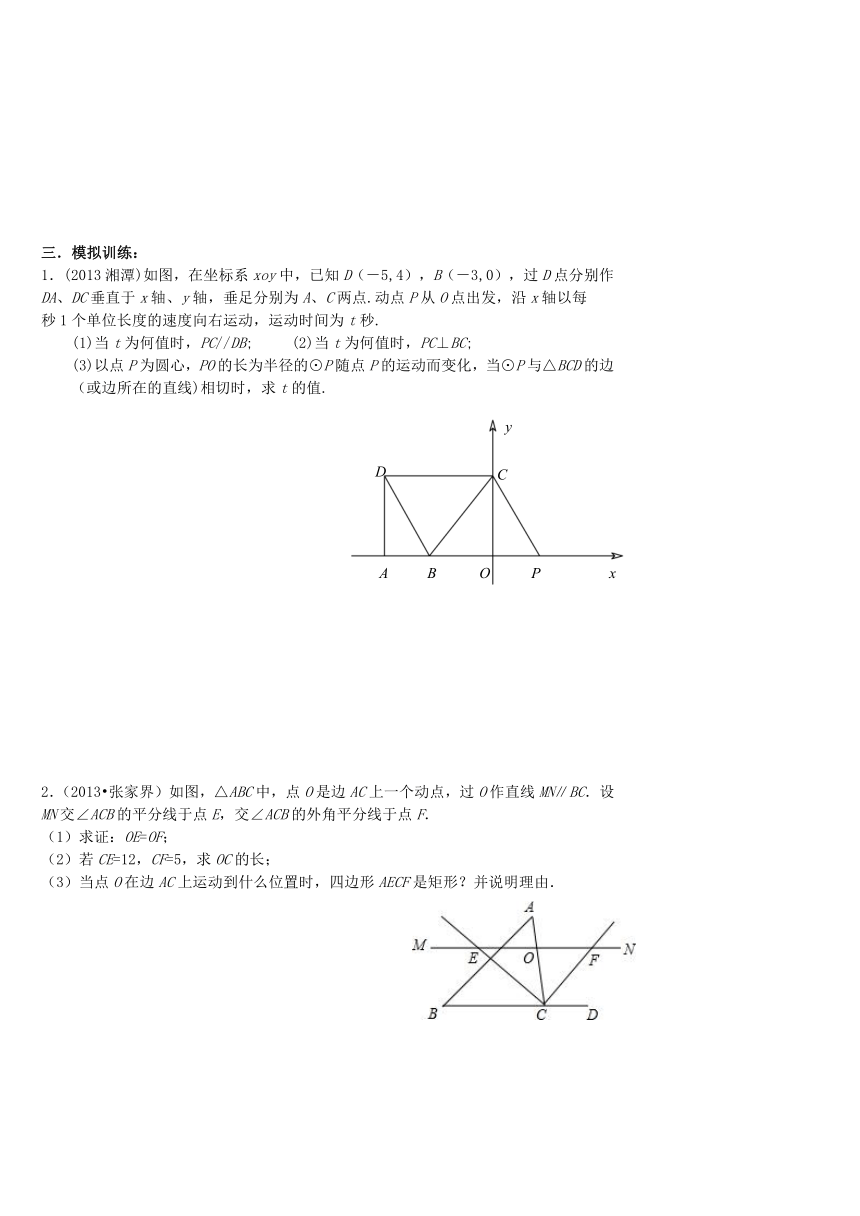
1.(2013湘潭)如图,在坐标系xoy中,已知D(-5,4),B(-3,0),过D点分别作
DA、DC垂直于x轴、y轴,垂足分别为A、C两点.动点P从O点出发,沿x轴以每
秒1个单位长度的速度向右运动,运动时间为t秒.
(1)当t为何值时,PC//DB; (2)当t为何值时,PC⊥BC;
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边
(或边所在的直线)相切时,求t的值.
2.(2013 张家界)如图,△ABC中, ( http: / / www.21cnjy.com )点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
( http: / / www.21cnjy.com )
3.(2013永州)如图,已知AB HYPERLINK "http://www.21cnjy.com" BD,CD HYPERLINK "http://www.21cnjy.com" BD
(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB= HYPERLINK "http://www.21cnjy.com" ,CD= HYPERLINK "http://www.21cnjy.com" ,BD= HYPERLINK "http://www.21cnjy.com" ,请问 HYPERLINK "http://www.21cnjy.com" 满足什么关系时,存在以P、A、B三点为顶点
的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
4.(2013 衡阳)如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,
垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线DM最长,并求出此时DM的值.
( http: / / www.21cnjy.com )
6.(2013怀化)如图10,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从A点、
C点同时出发,均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。
⑴经过几秒首次可使EF⊥AC?
⑵若EF⊥AC,在线段AC上,是否存在一点P,使 ( http: / / www.21cnjy.com )?若存在,请说
明P点的位置,并予以证明;若不存在,请说明理由。
7.(2013娄底)如图,在 HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,高 HYPERLINK "http://www.21cnjy.com" ,矩形 HYPERLINK "http://www.21cnjy.com" 的一边
HYPERLINK "http://www.21cnjy.com" 在 HYPERLINK "http://www.21cnjy.com" 边上, HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别在 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上, HYPERLINK "http://www.21cnjy.com" 交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)设 HYPERLINK "http://www.21cnjy.com" ,当 HYPERLINK "http://www.21cnjy.com" 为何值时,矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大?并求出最大面积;
(3)当矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大时,该矩形 HYPERLINK "http://www.21cnjy.com" 以每秒1个单位的速度沿射线 HYPERLINK "http://www.21cnjy.com" 匀速向上
运动(当矩形的边 HYPERLINK "http://www.21cnjy.com" 到达 HYPERLINK "http://www.21cnjy.com" 点时停止运动),设运动时间为 HYPERLINK "http://www.21cnjy.com" 秒,矩形 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 重
叠部分的面积为 HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 的函数关系式,并写出 HYPERLINK "http://www.21cnjy.com" 的取值范围.
( http: / / www.21cnjy.com )
四.填空题:
1.代数式x -2x+3的最小值是
2.正方形的边长为2,为的中点,是上一动点.连结,由正方形对称性
可知, 与关于直线对称.连结交于,则的最小值是___________.
3.如下左图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,
在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 。
4.如上中图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,
CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为___________.
5.如上右图,锐角△ABC的边AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N
分别是AD和AB上的动点,则BM+MN的最小值是___________.
五、路径最短问题(两点间连线中,直线段最短)
1.如图,圆柱形的桶外,有 ( http: / / www.21cnjy.com )一只蚂蚁从桶外的A点爬到桶内的B点处寻找食物,已知点A到桶口的距离AC为12cm,点B到桶口的距离BD为8cm,CD的长为15cm,那么蚂蚁爬行的最短路程是___________.
2.如图,是一个三级台阶,它的每一级的 ( http: / / www.21cnjy.com )长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是___________.
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
3.如图是一块长、宽、高分别是4c ( http: / / www.21cnjy.com )m、2cm和1cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到C1处吃食物,那么它需要爬行的最短路线的长是___________.
4.如图所示,有一圆锥形粮堆,其正 ( http: / / www.21cnjy.com )视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是___________米(结果不取近似值)
六.综合题中的动点最值问题:
已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,
其中A(-3,0)、C(0,-2).
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标.
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交
x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数
关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
O
O
P
A
B
C
D
y
x
一.株洲最近几年中考试题:
年 份 内 容 分值
2013年中考 相似三角形的判定与性质; 8分
2012年中考 相似三角形的判定与性质;二次函数的最值。 8分
2011年中考 △全等的判定;勾股定理。 8分
2010年中考 相似三角形的判定与性质;二次函数的最值。 8分
2009年中考 相似三角形的判定与性质;二次函数的最值。 10分
二.中考真题:
1.(2013 株洲)已知在△ABC中, ( http: / / www.21cnjy.com )∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
( http: / / www.21cnjy.com )
2.(2012 株洲)如图,在△ABC中, ( http: / / www.21cnjy.com )∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
( http: / / www.21cnjy.com )
3.(2010年株洲)(本题满分8分)如图,直角 HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,
HYPERLINK "http://www.21cnjy.com" ,点 HYPERLINK "http://www.21cnjy.com" 为边 HYPERLINK "http://www.21cnjy.com" 上一动点, HYPERLINK "http://www.21cnjy.com" ∥ HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" ,连结 HYPERLINK "http://www.21cnjy.com" .
(1)求 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 的长;
(2)设 HYPERLINK "http://www.21cnjy.com" 的长为 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 的面积为 HYPERLINK "http://www.21cnjy.com" .当 HYPERLINK "http://www.21cnjy.com" 为何值时, HYPERLINK "http://www.21cnjy.com" 最大,并求出最大值.
4.(2011株洲)如图,矩形 HYPERLINK "http://www.21cnjy.com" 中,点 HYPERLINK "http://www.21cnjy.com" 是线段 HYPERLINK "http://www.21cnjy.com" 上一动点, HYPERLINK "http://www.21cnjy.com" 为 HYPERLINK "http://www.21cnjy.com" 的中点, HYPERLINK "http://www.21cnjy.com"
的延长线交 HYPERLINK "http://www.21cnjy.com" 于 HYPERLINK "http://www.21cnjy.com" .(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)若 HYPERLINK "http://www.21cnjy.com" 厘米, HYPERLINK "http://www.21cnjy.com" 厘米, HYPERLINK "http://www.21cnjy.com" 从点 HYPERLINK "http://www.21cnjy.com" 出发,
以1厘米/秒的速度向 HYPERLINK "http://www.21cnjy.com" 运动(不与 HYPERLINK "http://www.21cnjy.com" 重合).
设点 HYPERLINK "http://www.21cnjy.com" 运动时间为 HYPERLINK "http://www.21cnjy.com" 秒,请用 HYPERLINK "http://www.21cnjy.com" 表示 HYPERLINK "http://www.21cnjy.com" 的长;
并求 HYPERLINK "http://www.21cnjy.com" 为何值时,四边形 HYPERLINK "http://www.21cnjy.com" 是菱形.
5.(2009年株洲)(本题满分10分)如图1, HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,点 HYPERLINK "http://www.21cnjy.com"
在线段 HYPERLINK "http://www.21cnjy.com" 上运动,点 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别在线段 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上,且使得四边形 HYPERLINK "http://www.21cnjy.com" 是矩形.设
HYPERLINK "http://www.21cnjy.com" 的长为 HYPERLINK "http://www.21cnjy.com" ,矩形 HYPERLINK "http://www.21cnjy.com" 的面积为 HYPERLINK "http://www.21cnjy.com" ,已知 HYPERLINK "http://www.21cnjy.com" 是 HYPERLINK "http://www.21cnjy.com" 的函数,其图象是过点(12,36)的
抛物线的一部分(如图2所示). (1)求 HYPERLINK "http://www.21cnjy.com" 的长;
(2)当 HYPERLINK "http://www.21cnjy.com" 为何值时,矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大,并求出最大值.
为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论:
张明:图2中的抛物线过点(12,36)在图1中表示什么呢?
李明:因为抛物线上的点是表示图1中的长与矩形面积的对应关系,
那么,(12,36)表示当时,的长与矩形面积的对应关系.
赵明:对,我知道纵坐标36是什么意思了!
孔明:哦,这样就可以算出,这个问题就可以解决了.
请根据上述对话,帮他们解答这个问题.
三.模拟训练:
1.(2013湘潭)如图,在坐标系xoy中,已知D(-5,4),B(-3,0),过D点分别作
DA、DC垂直于x轴、y轴,垂足分别为A、C两点.动点P从O点出发,沿x轴以每
秒1个单位长度的速度向右运动,运动时间为t秒.
(1)当t为何值时,PC//DB; (2)当t为何值时,PC⊥BC;
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边
(或边所在的直线)相切时,求t的值.
2.(2013 张家界)如图,△ABC中, ( http: / / www.21cnjy.com )点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
( http: / / www.21cnjy.com )
3.(2013永州)如图,已知AB HYPERLINK "http://www.21cnjy.com" BD,CD HYPERLINK "http://www.21cnjy.com" BD
(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP;若不存在,请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=9,CD=4,BD=15,请问在BD上存在多少个P点,使以P、A、B三点为顶点的
三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(4)若AB= HYPERLINK "http://www.21cnjy.com" ,CD= HYPERLINK "http://www.21cnjy.com" ,BD= HYPERLINK "http://www.21cnjy.com" ,请问 HYPERLINK "http://www.21cnjy.com" 满足什么关系时,存在以P、A、B三点为顶点
的三角形与以P、C、D三点为顶点的三角形相似的一个P点?两个P点?三个P点?
4.(2013 衡阳)如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,
垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线DM最长,并求出此时DM的值.
( http: / / www.21cnjy.com )
6.(2013怀化)如图10,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从A点、
C点同时出发,均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。
⑴经过几秒首次可使EF⊥AC?
⑵若EF⊥AC,在线段AC上,是否存在一点P,使 ( http: / / www.21cnjy.com )?若存在,请说
明P点的位置,并予以证明;若不存在,请说明理由。
7.(2013娄底)如图,在 HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,高 HYPERLINK "http://www.21cnjy.com" ,矩形 HYPERLINK "http://www.21cnjy.com" 的一边
HYPERLINK "http://www.21cnjy.com" 在 HYPERLINK "http://www.21cnjy.com" 边上, HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 分别在 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 上, HYPERLINK "http://www.21cnjy.com" 交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)设 HYPERLINK "http://www.21cnjy.com" ,当 HYPERLINK "http://www.21cnjy.com" 为何值时,矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大?并求出最大面积;
(3)当矩形 HYPERLINK "http://www.21cnjy.com" 的面积最大时,该矩形 HYPERLINK "http://www.21cnjy.com" 以每秒1个单位的速度沿射线 HYPERLINK "http://www.21cnjy.com" 匀速向上
运动(当矩形的边 HYPERLINK "http://www.21cnjy.com" 到达 HYPERLINK "http://www.21cnjy.com" 点时停止运动),设运动时间为 HYPERLINK "http://www.21cnjy.com" 秒,矩形 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 重
叠部分的面积为 HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 的函数关系式,并写出 HYPERLINK "http://www.21cnjy.com" 的取值范围.
( http: / / www.21cnjy.com )
四.填空题:
1.代数式x -2x+3的最小值是
2.正方形的边长为2,为的中点,是上一动点.连结,由正方形对称性
可知, 与关于直线对称.连结交于,则的最小值是___________.
3.如下左图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,
在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 。
4.如上中图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,
CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为___________.
5.如上右图,锐角△ABC的边AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N
分别是AD和AB上的动点,则BM+MN的最小值是___________.
五、路径最短问题(两点间连线中,直线段最短)
1.如图,圆柱形的桶外,有 ( http: / / www.21cnjy.com )一只蚂蚁从桶外的A点爬到桶内的B点处寻找食物,已知点A到桶口的距离AC为12cm,点B到桶口的距离BD为8cm,CD的长为15cm,那么蚂蚁爬行的最短路程是___________.
2.如图,是一个三级台阶,它的每一级的 ( http: / / www.21cnjy.com )长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是___________.
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com"
3.如图是一块长、宽、高分别是4c ( http: / / www.21cnjy.com )m、2cm和1cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到C1处吃食物,那么它需要爬行的最短路线的长是___________.
4.如图所示,有一圆锥形粮堆,其正 ( http: / / www.21cnjy.com )视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是___________米(结果不取近似值)
六.综合题中的动点最值问题:
已知:抛物线的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,
其中A(-3,0)、C(0,-2).
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标.
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交
x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数
关系式.试说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
O
O
P
A
B
C
D
y
x
同课章节目录
